Misplaced Pages

In physics, a perfect fluid or ideal fluid is a fluid that can be completely characterized by its rest frame mass density ${\displaystyle \rho _{m}}$ and isotropic pressure ⁠${\displaystyle p}$⁠. Real fluids are "sticky" and contain (and conduct) heat. Perfect fluids are idealized models in which these possibilities are ignored. Specifically, perfect fluids have no shear stresses, viscosity, or heat conduction. The closest-known substance to a perfect fluid is quark–gluon plasma.

D'Alembert paradox

In classical mechanics, ideal fluids are described by Euler equations. Ideal fluids produce no drag according to d'Alembert's paradox.

Relativistic formulation

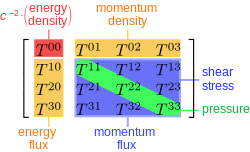
In space-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{m}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }+p\,\eta ^{\mu \nu },}$

where U is the 4-velocity vector field of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (-1,1,1,1)}$ is the metric tensor of Minkowski spacetime.

In time-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{\text{m}}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }-p\,\eta ^{\mu \nu },}$

where ${\displaystyle U}$ is the 4-velocity of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (1,-1,-1,-1)}$ is the metric tensor of Minkowski spacetime.

This takes on a particularly simple form in the rest frame

${\displaystyle \left}$

where ${\displaystyle \rho _{\text{e}}=\rho _{\text{m}}c^{2}}$ is the energy density and ${\displaystyle p}$ is the pressure of the fluid.

Perfect fluids admit a Lagrangian formulation, which allows the techniques used in field theory, in particular, quantization, to be applied to fluids.

Perfect fluids are used in general relativity to model idealized distributions of matter, such as the interior of a star or an isotropic universe. In the latter case, the equation of state of the perfect fluid may be used in Friedmann–Lemaître–Robertson–Walker equations to describe the evolution of the universe.

In general relativity, the expression for the stress–energy tensor of a perfect fluid is written as

${\displaystyle T^{\mu \nu }=\left(\rho _{m}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }+p\,g^{\mu \nu },}$

where ${\displaystyle U}$ is the 4-velocity vector field of the fluid and where ${\displaystyle g^{\mu \nu }}$ is the inverse metric, written with a space-positive signature.

See also

• Equation of state
• Ideal gas
• Fluid solutions in general relativity
• Potential flow

Notes

1. Usually, "perfect fluid" is reserved for relativistic models and "ideal fluid" for classical inviscid flow.

References

• S.W. Hawking; G.F.R. Ellis (1973), The Large Scale Structure of Space-Time, Cambridge University Press ISBN 0-521-20016-4, ISBN 0-521-09906-4 (pbk.)
• WA Zajc (2008). "The fluid nature of quark–gluon plasma". Nuclear Physics A. 805 (1–4): 283c – 294c. arXiv:0802.3552. Bibcode:2008NuPhA.805..283Z. doi:10.1016/j.nuclphysa.2008.02.285. S2CID 119273920.

• Fluid mechanics
• Superfluidity
• Physics