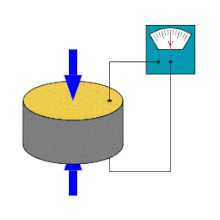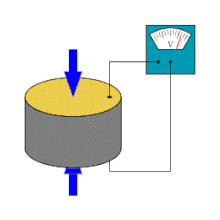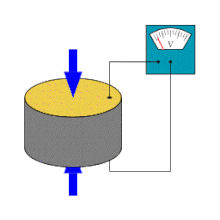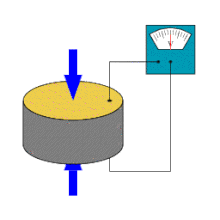
A piezoelectric sensor is a device that uses the piezoelectric effect to measure changes in pressure, acceleration, temperature, strain, or force by converting them to an electrical charge. The prefix piezo- is Greek for 'press' or 'squeeze'.
Applications
Piezoelectric sensors are versatile tools for the measurement of various processes. They are used for quality assurance, process control, and for research and development in many industries. Jacques and Pierre Curie discovered the piezoelectric effect in 1880, but only in the 1950s did manufacturers begin to use the piezoelectric effect in industrial sensing applications. Since then, this measuring principle has been increasingly used, and has become a mature technology with excellent inherent reliability.
They have been successfully used in various applications, such as in medical, aerospace, nuclear instrumentation, and as a tilt sensor in consumer electronics or a pressure sensor in the touch pads of mobile phones. In the automotive industry, piezoelectric elements are used to monitor combustion when developing internal combustion engines. The sensors are either directly mounted into additional holes into the cylinder head or the spark/glow plug is equipped with a built-in miniature piezoelectric sensor.
The rise of piezoelectric technology is directly related to a set of inherent advantages. The high modulus of elasticity of many piezoelectric materials is comparable to that of many metals and goes up to 10 N/m. Even though piezoelectric sensors are electromechanical systems that react to compression, the sensing elements show almost zero deflection. This gives piezoelectric sensors ruggedness, an extremely high natural frequency and an excellent linearity over a wide amplitude range. Additionally, piezoelectric technology is insensitive to electromagnetic fields and radiation, enabling measurements under harsh conditions. Some materials used (especially gallium phosphate or tourmaline) are extremely stable at high temperatures, enabling sensors to have a working range of up to 1000 °C. Tourmaline shows pyroelectricity in addition to the piezoelectric effect; this is the ability to generate an electrical signal when the temperature of the crystal changes. This effect is also common to piezoceramic materials. Gautschi in Piezoelectric Sensorics (2002) offers this comparison table of characteristics of piezo sensor materials vs other types:
| Principle | Strain sensitivity |
Threshold |
Span to threshold ratio |
|---|---|---|---|
| Piezoelectric | 5.0 | 0.00001 | 100,000,000 |
| Piezoresistive | 0.0001 | 0.0001 | 2,500,000 |
| Inductive | 0.001 | 0.0005 | 2,000,000 |
| Capacitive | 0.005 | 0.0001 | 750,000 |
| Resistive | 0.000005 | 0.01 | 50,000 |
One disadvantage of piezoelectric sensors is that they cannot be used for truly static measurements. A static force results in a fixed amount of charge on the piezoelectric material. In conventional readout electronics, imperfect insulating materials and reduction in internal sensor resistance causes a constant loss of electrons and yields a decreasing signal. Elevated temperatures cause an additional drop in internal resistance and sensitivity. The main effect on the piezoelectric effect is that with increasing pressure loads and temperature, the sensitivity reduces due to twin formation. While quartz sensors must be cooled during measurements at temperatures above 300 °C, special types of crystals like GaPO4 gallium phosphate show no twin formation up to the melting point of the material itself.
However, it is not true that piezoelectric sensors can only be used for very fast processes or at ambient conditions. In fact, numerous piezoelectric applications produce quasi-static measurements, and other applications work in temperatures higher than 500 °C.
Piezoelectric sensors can also be used to determine aromas in the air by simultaneously measuring resonance and capacitance. Computer controlled electronics vastly increase the range of potential applications for piezoelectric sensors.
Piezoelectric sensors are also seen in nature. The collagen in bone is piezoelectric, and is thought by some to act as a biological force sensor. Piezoelectricity has also been shown in the collagen of soft tissue such as the Achilles tendon, aortic walls, and heart valves.
Principle of operation
The way a piezoelectric material is cut defines one of its three main operational modes:
- Transverse
- Longitudinal
- Shear
Transverse effect
A force applied along a neutral axis (y) displaces charges along the (x) direction, perpendicular to the line of force. The amount of charge () depends on the geometrical dimensions of the respective piezoelectric element. When dimensions apply,
- ,
- where is the dimension in line with the neutral axis, is in line with the charge generating axis and is the corresponding piezoelectric coefficient.
Longitudinal effect
The amount of charge displaced is strictly proportional to the applied force and independent of the piezoelectric element size and shape. Putting several elements mechanically in series and electrically in parallel is the only way to increase the charge output. The resulting charge is
- ,
- where is the piezoelectric coefficient for a charge in x-direction released by forces applied along x-direction (in pC/N). is the applied Force in x-direction and corresponds to the number of stacked elements.
Shear effect
The charge produced is exactly proportional to the applied force and is generated at a right angle to the force. The charge is independent of the element size and shape. For elements mechanically in series and electrically in parallel the charge is
- .
In contrast to the longitudinal and shear effects, the transverse effect make it possible to fine-tune sensitivity on the applied force and element dimension.
Electrical properties
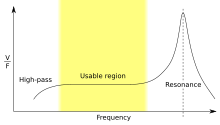
A piezoelectric transducer can be modeled as a voltage source with a filter. The voltage V at the source is directly proportional to the applied force, pressure, or strain. The output signal is related to this mechanical force as if it had passed through the filter, which gives the transducer a very high and frequency-dependent output impedance, which results in a frequency response similar to Figure 1.
Mechanical–electrical analogy
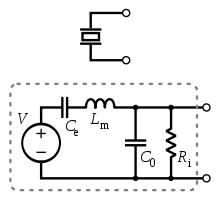
Figure 2's detailed model includes the effects of the sensor's mechanical construction and other non-idealities. The inductance Lm is due to the seismic mass and inertia of the sensor itself. Ce is inversely proportional to the mechanical elasticity of the sensor. C0 represents the static capacitance of the transducer, resulting from an inertial mass of infinite size. These inductances and capacitances are not real electrical elements of the transducer, but rather act as a mechanical–electrical analogy.
Ri however is an actual electric resistance representing the insulation leakage resistance of the transducer. If the sensor is connected to a load resistance, this also acts in parallel with the insulation resistance, both increasing the high-pass cutoff frequency. Also not shown in this schematic is the actual capacitance of the sensor surface itself.
Simplified model

Piezo sensors typically use the flat region of the frequency response (the "usable region" in Figure 1) between the high-pass cutoff and the resonant peak. The load and leakage resistance must be large enough that low frequencies of interest are not lost. A simplified equivalent circuit model (top of Figure 3) can be used in this region, in which Cs represents the capacitance of the sensor surface itself, determined by the standard formula for capacitance of parallel plates. This simplified model's Norton equivalent (bottom of Figure 3) is a charge source in parallel with the source capacitance, with the charge directly proportional to the applied force.
Sensor design

Piezoelectric technology can measure various physical quantities, most commonly pressure and acceleration. For pressure sensors, a thin membrane and a massive base is used, ensuring that an applied pressure specifically loads the elements in one direction. For accelerometers, a seismic mass is attached to the crystal elements. When the accelerometer experiences a motion, the invariant seismic mass loads the elements according to Newton's second law of motion .
The main difference in working principle between these two cases is the way they apply forces to the sensing elements. In a pressure sensor, a thin membrane transfers the force to the elements, while in accelerometers an attached seismic mass applies the forces. Sensors often tend to be sensitive to more than one physical quantity. Pressure sensors show false signal when they are exposed to vibrations. Sophisticated pressure sensors therefore use acceleration compensation elements in addition to the pressure sensing elements. By carefully matching those elements, the acceleration signal (released from the compensation element) is subtracted from the combined signal of pressure and acceleration to derive the true pressure information.
Vibration sensors can also harvest otherwise wasted energy from mechanical vibrations. This is accomplished by using piezoelectric materials to convert mechanical strain into usable electrical energy.
Sensing materials
Three main groups of materials are used for piezoelectric sensors: piezoelectric ceramics, single crystal materials and thin film piezoelectric materials. The ceramic materials (such as PZT ceramic) have a piezoelectric constant/sensitivity that is roughly two orders of magnitude higher than those of the natural single crystal materials and can be produced by inexpensive sintering processes. The piezoeffect in piezoceramics is "trained", so their high sensitivity degrades over time. This degradation is highly correlated with increased temperature.
The less-sensitive, natural, single-crystal materials (gallium phosphate, quartz, tourmaline) have a higher – when carefully handled, almost unlimited – long term stability. There are also new single-crystal materials commercially available such as Lead Magnesium Niobate-Lead Titanate (PMN-PT). These materials offer improved sensitivity over PZT but have a lower maximum operating temperature and are currently more complicated to manufacture due to four compound vs. three compound material PZT.
Thin film piezoelectric materials can be manufactured utilizing sputtering, CVD (chemical vapour deposition), ALD (atomic layer epitaxy) etc. methods. Thin film piezoelectric materials are used in applications where high frequency (> 100 MHz) is utilised in the measurement method and/or small size is favored in the application.
Self-sensing materials with an aluminum matrix and embedded piezoelectric phases, such as PZT (lead zirconate titanate) or barium titanate, can be produced through Friction Stir Processing (FSP). In this process, the piezoelectric particles are dispersed into the aluminum matrix, creating a composite material capable of both structural and sensing functions. The piezoelectric particles generate an electrical signal in response to mechanical stress or strain, enabling the material to monitor its own condition. FSP ensures a fine dispersion of the piezoelectric phase and enhances the bonding between particles and the matrix, leading to improved mechanical and sensing properties.
See also
- Charge amplifier
- List of sensors
- Piezoelectricity
- Piezoelectric speaker
- Piezoresistive effect
- Ultrasonic homogenizer
- Ultrasonic transducer
- Thin-film bulk acoustic resonator
References
- Platt, Charles (2012). Encyclopedia of electronic components. Volume 1, [Power sources & conversion : resistors, capacitors, inductors, switches, encoders, relays, transistors]. Sebastopol CA: O'Reilly/Make. p. 258. ISBN 978-1-4493-3387-4. OCLC 824752425.
- Jiao, Pengcheng; Egbe, King-James I.; Xie, Yiwei; Matin Nazar, Ali; Alavi, Amir H. (2020-07-03). "Piezoelectric Sensing Techniques in Structural Health Monitoring: A State-of-the-Art Review". Sensors. 20 (13): 3730. Bibcode:2020Senso..20.3730J. doi:10.3390/s20133730. ISSN 1424-8220. PMC 7374461. PMID 32635286.
- Curie, Jacques; Curie, Pierre (1880). "Développement par compression de l'électricité polaire dans les cristaux hémièdres à faces inclinées". Bulletin de la Société Minéralogique de France. 3 (4): 90–93. doi:10.3406/bulmi.1880.1564.
- "Research & Development". Facialteam. 15 November 2021. Retrieved February 20, 2023.
- P. Moubarak, et al., A Self-Calibrating Mathematical Model for the Direct Piezoelectric Effect of a New MEMS Tilt Sensor, IEEE Sensors Journal, 12 (5) (2011) 1033 – 1042.
- , Archived December 3, 2008, at the Wayback Machine
- Wali, R Paul (October 2012). "An electronic nose to differentiate aromatic flowers using a real-time information-rich piezoelectric resonance measurement". Procedia Chemistry. 6: 194–202. doi:10.1016/j.proche.2012.10.146.
- Lakes, Roderic (July 8, 2013). "Electrical Properties of Bone - a review". University of Wisconsin. Retrieved September 1, 2013.
- Becker, Robert O.; Marino, Andrew A. "Piezoelectricity". Department of Orthopaedic Surgery at Louisiana State University Health Sciences Center. Archived from the original on August 2, 2009. Retrieved September 1, 2013.
- Rini, Matteo (2019). "Soft Biological Tissues Can Be Piezoelectric". Physics. 12. Bibcode:2019PhyOJ..12S.138.. doi:10.1103/Physics.12.s138. S2CID 240900893.
- ^ "Interfacing Piezo Film to Electronics" (PDF). Measurement Specialties. March 2006. Archived from the original (PDF) on 2012-04-26. Retrieved December 2, 2007.
- ^ Alfredo Vázquez Carazo (January 2000). "Novel Piezoelectric Transducers for High Voltage Measurements" (Document). Universitat Politècnica de Catalunya. p. 242.
- Karki, James (September 2000). "Signal Conditioning Piezoelectric Sensors" (PDF). Texas Instruments. Retrieved December 2, 2007.
- Keim, Robert (2018-10-15). "Understanding and Modeling Piezoelectric Sensors". All About Circuits. Archived from the original on 2022-12-02. Retrieved 2022-12-02.
- Ludlow, Chris (May 2008). "Energy Harvesting with Piezoelectric Sensors" (PDF). Mide Technology. Retrieved May 21, 2008.
- Ferreira, Pedro M.; Machado, Miguel A.; Carvalho, Marta S.; Vilaça, Pedro; Sorger, Gonçalo; Pinto, Joana Vaz; Deuermeier, Jonas; Vidal, Catarina (November 2023). "Self-sensing metallic material based on PZT particles produced by friction stir processing envisaging structural health monitoring applications". Materials Characterization. 205: 113371. doi:10.1016/j.matchar.2023.113371. hdl:10362/162424.
- Ferreira, Pedro M.; Machado, Miguel A.; Carvalho, Marta S.; Vidal, Catarina (February 2023). "Granting Sensorial Properties to Metal Parts through Friction Stir Processing". Measurement. 207: 112405. Bibcode:2023Meas..20712405F. doi:10.1016/j.measurement.2022.112405. hdl:10362/147039.
- Ferreira, Pedro M; Caçador, David; Machado, Miguel A; Carvalho, Marta S; Vilaça, Pedro; Sorger, Gonçalo; Farias, Francisco Werley Cipriano; Figueiredo, Arthur Ribeiro; Vidal, Catarina (2024-06-01). "Enabling electrical response through piezoelectric particle integration in AA2017-T451 aluminium parts using FSP technology". Smart Materials and Structures. 33 (6): 065037. Bibcode:2024SMaS...33f5037F. doi:10.1088/1361-665X/ad4d45. hdl:10362/170279. ISSN 0964-1726.
- Ferreira, Pedro M.; Meireles, Afonso; Vidal, Catarina; Carvalho, Marta S.; Machado, Miguel A. (July 2024). "Evaluation of self-sensing material behaviour: Insights from cyclic and pulse load testing". Measurement. 234: 114878. Bibcode:2024Meas..23414878F. doi:10.1016/j.measurement.2024.114878. hdl:10362/170278.
External links
- Material constants of gallium phosphate
- The basic functional principle of a piezoelectric accelerometer
 ) depends on the geometrical dimensions of the respective piezoelectric element. When dimensions
) depends on the geometrical dimensions of the respective piezoelectric element. When dimensions  apply,
apply,
 ,
, is the dimension in line with the neutral axis,
is the dimension in line with the neutral axis,  is in line with the charge generating axis and
is in line with the charge generating axis and  is the corresponding piezoelectric coefficient.
is the corresponding piezoelectric coefficient. ,
, is the piezoelectric coefficient for a charge in x-direction released by forces applied along x-direction (in
is the piezoelectric coefficient for a charge in x-direction released by forces applied along x-direction (in  is the applied Force in x-direction and
is the applied Force in x-direction and  corresponds to the number of stacked elements.
corresponds to the number of stacked elements. .
. .
.