Plasma oscillations, also known as Langmuir waves (after Irving Langmuir), are rapid oscillations of the electron density in conducting media such as plasmas or metals in the ultraviolet region. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency depends only weakly on the wavelength of the oscillation. The quasiparticle resulting from the quantization of these oscillations is the plasmon.
Langmuir waves were discovered by American physicists Irving Langmuir and Lewi Tonks in the 1920s. They are parallel in form to Jeans instability waves, which are caused by gravitational instabilities in a static medium.
Mechanism
Consider an electrically neutral plasma in equilibrium, consisting of a gas of positively charged ions and negatively charged electrons. If one displaces by a tiny amount an electron or a group of electrons with respect to the ions, the Coulomb force pulls the electrons back, acting as a restoring force.
'Cold' electrons
If the thermal motion of the electrons is ignored, it is possible to show that the charge density oscillates at the plasma frequency
where is the number density of electrons, is the electric charge, is the effective mass of the electron, and is the permittivity of free space. Note that the above formula is derived under the approximation that the ion mass is infinite. This is generally a good approximation, as the electrons are so much lighter than ions.
Proof using Maxwell equations. Assuming charge density oscillations the continuity equation: the Gauss law and the conductivity taking the divergence on both sides and substituting the above relations: which is always true only if But this is also the dielectric constant (see Drude Model) and the condition of transparency (i.e. from a certain plasma frequency and above), the same condition here apply to make possible also the propagation of density waves in the charge density.
This expression must be modified in the case of electron-positron plasmas, often encountered in astrophysics. Since the frequency is independent of the wavelength, these oscillations have an infinite phase velocity and zero group velocity.
Note that, when , the plasma frequency, , depends only on physical constants and electron density . The numeric expression for angular plasma frequency is
Metals are only transparent to light with a frequency higher than the metal's plasma frequency. For typical metals such as aluminium or silver, is approximately 10 cm, which brings the plasma frequency into the ultraviolet region. This is why most metals reflect visible light and appear shiny.
'Warm' electrons
When the effects of the electron thermal speed are taken into account, the electron pressure acts as a restoring force as well as the electric field and the oscillations propagate with frequency and wavenumber related by the longitudinal Langmuir wave: called the Bohm–Gross dispersion relation. If the spatial scale is large compared to the Debye length, the oscillations are only weakly modified by the pressure term, but at small scales the pressure term dominates and the waves become dispersionless with a speed of . For such waves, however, the electron thermal speed is comparable to the phase velocity, i.e., so the plasma waves can accelerate electrons that are moving with speed nearly equal to the phase velocity of the wave. This process often leads to a form of collisionless damping, called Landau damping. Consequently, the large-k portion in the dispersion relation is difficult to observe and seldom of consequence.
In a bounded plasma, fringing electric fields can result in propagation of plasma oscillations, even when the electrons are cold.
In a metal or semiconductor, the effect of the ions' periodic potential must be taken into account. This is usually done by using the electrons' effective mass in place of m.
Plasma oscillations and the effect of the negative mass

Plasma oscillations may give rise to the effect of the “negative mass”. The mechanical model giving rise to the negative effective mass effect is depicted in Figure 1. A core with mass is connected internally through the spring with constant to a shell with mass . The system is subjected to the external sinusoidal force . If we solve the equations of motion for the masses and and replace the entire system with a single effective mass we obtain: where . When the frequency approaches from above the effective mass will be negative.
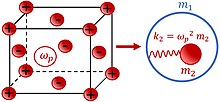
The negative effective mass (density) becomes also possible based on the electro-mechanical coupling exploiting plasma oscillations of a free electron gas (see Figure 2). The negative mass appears as a result of vibration of a metallic particle with a frequency of which is close the frequency of the plasma oscillations of the electron gas relatively to the ionic lattice . The plasma oscillations are represented with the elastic spring , where is the plasma frequency. Thus, the metallic particle vibrated with the external frequency ω is described by the effective mass which is negative when the frequency approaches from above. Metamaterials exploiting the effect of the negative mass in the vicinity of the plasma frequency were reported.
See also
- Electron wake
- Plasmon
- Relativistic quantum chemistry
- Surface plasmon resonance
- Upper hybrid oscillation, in particular for a discussion of the modification to the mode at propagation angles oblique to the magnetic field
- Waves in plasmas
References
- Tonks, Lewi; Langmuir, Irving (1929). "Oscillations in ionized gases" (PDF). Physical Review. 33 (8): 195–210. Bibcode:1929PhRv...33..195T. doi:10.1103/PhysRev.33.195. PMC 1085653.
- Ashcroft, Neil; Mermin, N. David (1976). Solid State Physics. New York: Holt, Rinehart and Winston. p. 19. ISBN 978-0-03-083993-1.
- Fu, Ying (2011). Optical properties of nanostructures. Pan Stanford. p. 201.
- *Andreev, A. A. (2000), An Introduction to Hot Laser Plasma Physics, Huntington, New York: Nova Science Publishers, Inc., ISBN 978-1-56072-803-0
- ^ Milton, Graeme W; Willis, John R (2007-03-08). "On modifications of Newton's second law and linear continuum elastodynamics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 463 (2079): 855–880. Bibcode:2007RSPSA.463..855M. doi:10.1098/rspa.2006.1795. S2CID 122990527.
- ^ Chan, C. T.; Li, Jensen; Fung, K. H. (2006-01-01). "On extending the concept of double negativity to acoustic waves". Journal of Zhejiang University Science A. 7 (1): 24–28. doi:10.1631/jzus.2006.A0024. ISSN 1862-1775. S2CID 120899746.
- ^ Huang, H. H.; Sun, C. T.; Huang, G. L. (2009-04-01). "On the negative effective mass density in acoustic metamaterials". International Journal of Engineering Science. 47 (4): 610–617. doi:10.1016/j.ijengsci.2008.12.007. ISSN 0020-7225.
- ^ Yao, Shanshan; Zhou, Xiaoming; Hu, Gengkai (2008-04-14). "Experimental study on negative effective mass in a 1D mass–spring system". New Journal of Physics. 10 (4): 043020. Bibcode:2008NJPh...10d3020Y. doi:10.1088/1367-2630/10/4/043020. ISSN 1367-2630.
- ^ Bormashenko, Edward; Legchenkova, Irina (April 2020). "Negative Effective Mass in Plasmonic Systems". Materials. 13 (8): 1890. Bibcode:2020Mate...13.1890B. doi:10.3390/ma13081890. PMC 7215794. PMID 32316640.
 Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
- ^ Bormashenko, Edward; Legchenkova, Irina; Frenkel, Mark (August 2020). "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation". Materials. 13 (16): 3512. Bibcode:2020Mate...13.3512B. doi:10.3390/ma13163512. PMC 7476018. PMID 32784869.
Further reading
- Longair, Malcolm S. (1998), Galaxy Formation, Berlin: Springer, ISBN 978-3-540-63785-1
 (
( (
( is the
is the  is the
is the  is the
is the  is the
is the  the continuity equation:
the continuity equation:
 the Gauss law
the Gauss law
 and the conductivity
and the conductivity
 taking the divergence on both sides and substituting the above relations:
taking the divergence on both sides and substituting the above relations:
 which is always true only if
which is always true only if
 But this is also the dielectric constant (see
But this is also the dielectric constant (see  and the condition of transparency (i.e.
and the condition of transparency (i.e.  from a certain plasma frequency
from a certain plasma frequency  and above), the same condition here
and above), the same condition here  apply to make possible also the propagation of density waves in the charge density.
apply to make possible also the propagation of density waves in the charge density.
 , the plasma frequency,
, the plasma frequency,  , depends only on
, depends only on 
 are taken into account, the electron pressure acts as a restoring force as well as the electric field and the oscillations propagate with frequency and
are taken into account, the electron pressure acts as a restoring force as well as the electric field and the oscillations propagate with frequency and  called the
called the  . For such waves, however, the electron thermal speed is comparable to the
. For such waves, however, the electron thermal speed is comparable to the  so the plasma waves can
so the plasma waves can  is connected internally through the spring with
is connected internally through the spring with  to a shell with mass
to a shell with mass  . The system is subjected to the sinusoidal force
. The system is subjected to the sinusoidal force  .
. we obtain:
we obtain:
 where
where  . When the frequency
. When the frequency  approaches
approaches  from above the effective mass
from above the effective mass  , where
, where  which is negative when the frequency
which is negative when the frequency