
The plum pudding model was the first scientific model of the atom to describe an internal structure. It was first proposed by J. J. Thomson in 1904 following his discovery of the electron in 1897, and was rendered obsolete by Ernest Rutherford's discovery of the atomic nucleus in 1911. The model tried to account for two properties of atoms then known: that there are electrons, and that atoms have no net electric charge. Logically there had to be an equal amount of positive charge to balance out the negative charge of the electrons. As Thomson had no idea as to the source of this positive charge, he tentatively proposed that it was everywhere in the atom, and that the atom was spherical. This was the mathematically simplest hypothesis to fit the available evidence, or lack thereof. In such a sphere, the negatively charged electrons would distribute themselves in a more or less even manner throughout the volume, simultaneously repelling each other while being attracted to the positive sphere's center.
Despite Thomson's efforts, his model couldn't account for emission spectra and valencies. Based on experimental studies of alpha particle scattering (in the gold foil experiment), Ernest Rutherford developed an alternative model for the atom featuring a compact nucleus where the positive charge is concentrated.
Thomson's model is popularly referred to as the "plum pudding model" with the notion that the electrons are distributed uniformly like raisins in a plum pudding. Neither Thomson nor his colleagues ever used this analogy. It seems to have been coined by popular science writers to make the model easier to understand for the layman. The analogy is perhaps misleading because Thomson likened the positive sphere to a liquid rather than a solid since he thought the electrons moved around in it.
Significance
Thomson's model marks the moment when the development of atomic theory passed from chemists to physicists. While atomic theory was widely accepted by chemists by the end of the 19th century, physicists remained skeptical because the atomic model lacked any properties which concerned their field, such as electric charge, magnetic moment, volume, or absolute mass. Before Thomson's model, atoms were simply the basic units of weight by which the chemical elements react. Thomson himself was a physicist and his atomic model was a byproduct of his investigations of cathode rays, by which he discovered the negatively charged particles now known as electrons. Thomson hypothesized that the quantity, arrangement, and motions of electrons in the atom could explain its physical and chemical properties, such as emission spectra, valencies, reactivity, and ionization. He was on the right track, though his approach was based on classical mechanics and he did not have the insight to incorporate quantized energy into it.
Background
Main article: History of atomic theoryThroughout the 19th century evidence from chemistry and statistical mechanics accumulated that matter was composed of atoms. The structure of the atom was discussed, and by the end of the century the leading model was the vortex theory of the atom, proposed by William Thomson (later Lord Kelvin) in 1867. By 1890, J.J. Thomson had his own version called the "nebular atom" hypothesis, in which atoms were composed of immaterial vortices and suggested similarities between the arrangement of vortices and periodic regularity found among the chemical elements.
Thomson's discovery of the electron in 1897 changed his views. Thomson called them "corpuscles" (particles), but they were more commonly called "electrons", the name G. J. Stoney had coined for the "fundamental unit quantity of electricity" in 1891. However even late in 1899, few scientists believed in subatomic particles.
Another emerging scientific theme of the 19th century was the discovery and study of radioactivity. Thomson discovered the electron by studying cathode rays, and in 1900 Henri Becquerel determined that the radiation from uranium, now called beta particles, had the same charge/mass ratio as cathode rays. These beta particles were believed to be electrons travelling at high speed. The particles were used by Thomson to probe atoms to find evidence for his atomic theory. The other form of radiation critical to this era of atomic models was alpha particles. Heavier and slower than beta particles, these were the key tool used by Rutherford to find evidence against Thomson's model.
In addition to the emerging atomic theory, the electron, and radiation, the last element of history was the many studies of atomic spectra published in the late 19th century. Part of the attraction of the vortex model was its possible role in describing the spectral data as vibrational responses to electromagnetic radiation. Neither Thomson's model nor its successor, Rutherford's model, made progress towards understanding atomic spectra. That would have to wait until Niels Bohr built the first quantum-based atom model.
Development
Thomson's model was the first to assign a specific inner structure to an atom, though his earliest descriptions did not include mathematical formulas. From 1897 through 1913, Thomson proposed a series of increasingly detailed polyelectron models for the atom. His first versions were qualitative culminating in his 1906 paper and follow on summaries. Thomson's model changed over the course of its initial publication, finally becoming a model with much more mobility containing electrons revolving in the dense field of positive charge rather than a static structure. Thomson attempted unsuccessfully to reshape his model to account for some of the major spectral lines experimentally known for several elements.
1897 Corpuscles inside atoms
In a paper titled Cathode Rays, Thomson demonstrated that cathode rays are not light but made of negatively charged particles which he called corpuscles. He observed that cathode rays can be deflected by electric and magnetic fields, which does not happen with light rays. In a few paragraphs near the end of this long paper Thomson discusses the possibility that atoms were made of these corpuscles, calling them primordial atoms. Thomson believed that the intense electric field around the cathode caused the surrounding gas molecules to split up into their component corpuscles, thereby generating cathode rays. Thomson thus showed evidence that atoms were divisible, though he did not attempt to describe their structure at this point.
Thomson notes that he was not the first scientist to propose that atoms are divisible, making reference to William Prout who in 1815 found that the atomic weights of various elements were multiples of hydrogen's atomic weight and hypothesised that all atoms were made of hydrogen atoms fused together. Prout's hypothesis was dismissed by chemists when by the 1830s it was found that some elements seemed to have a non-integer atomic weight—e.g. chlorine has an atomic weight of about 35.45. But the idea continued to intrigue scientists. The discrepancies were eventually explained with the discovery of isotopes in 1912.
A few months after Thomson's paper appeared, George FitzGerald suggested that the corpuscle identified by Thomson from cathode rays and proposed as parts of an atom was a "free electron", as described by physicist Joseph Larmor and Hendrik Lorentz. While Thomson did not adopt the terminology, the connection convinced other scientists that cathode rays were particles, an important step in their eventual acceptance of an atomic model based on sub-atomic particles.
In 1899 Thomson reiterated his atomic model in a paper that showed that negative electricity created by ultraviolet light landing on a metal (known now as the photoelectric effect) has the same mass-to-charge ratio as cathode rays; then he applied his previous method for determining the charge on ions to the negative electric particles created by ultraviolet light. He estimated that the electron's mass was 0.0014 times that of the hydrogen ion (as a fraction: 1/714). In the conclusion of this paper he writes:
I regard the atom as containing a large number of smaller bodies which I shall call corpuscles; these corpuscles are equal to each other; the mass of a corpuscle is the mass of the negative ion in a gas at low pressure, i.e. about 3 × 10 of a gramme. In the normal atom, this assemblage of corpuscles forms a system which is electrically neutral. The negative effect is balanced by something which causes the space through which the corpuscles are spread to act as if it had a charge of positive electricity equal in amount to the sum of the negative charges on the corpuscles.
1904 Mechanical model of the atom
Thomson provided his first detailed description of the atom in his 1904 paper On the Structure of the Atom. Thomson starts with a short description of his model
... the atoms of the elements consist of a number of negatively electrified corpuscles enclosed in a sphere of uniform positive electrification, ...
Primarily focused on the electrons, Thomson adopted the positive sphere from Kelvin's atom model proposed a year earlier. He then gives a detailed mechanical analysis of such a system, distributing the electrons uniformly around a ring. The attraction of the positive electrification is balanced by the mutual repulsion of the electrons. His analysis focuses on stability, looking for cases where small changes in position are countered by restoring forces.
After discussing his many formulae for stability he turned to analysing patterns in the number of electrons in various concentric rings of stable configurations. These regular patterns Thomson argued are analogous to the periodic law of chemistry behind the structure of the periodic table. This concept, that a model based on subatomic particles could account for chemical trends, encouraged interest in Thomson's model and influenced future work even if the details Thomson's electron assignments turned out to be incorrect.
Thomson at this point believed that all the mass of the atom was carried by the electrons. This would mean that even a small atom would have to contain thousands of electrons, and the positive electrification that encapsulated them was without mass.
1905 lecture on electron arrangements
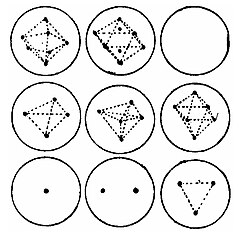 A 1905 diagram by J. J. Thomson illustrating his hypothetical arrangements of electrons in an atom, ranging from one to eight electrons.
A 1905 diagram by J. J. Thomson illustrating his hypothetical arrangements of electrons in an atom, ranging from one to eight electrons. Thomson's diagram of Mayer's practical experiment for exploring electron arrangements.
Thomson's diagram of Mayer's practical experiment for exploring electron arrangements.
In a lecture delivered to the Royal Institution of Great Britain in 1905, Thomson explained that it was too computationally difficult for him to calculate the movements of large numbers of electrons in the positive sphere, so he proposed a practical experiment. This involved magnetised pins pushed into cork discs and set afloat in a basin of water. The pins were oriented such that they repelled each other. Above the centre of the basin was suspended an electromagnet that attracted the pins. The equilibrium arrangement the pins took informed Thomson on what arrangements the electrons in an atom might take.
For instance, he observed that while five pins would arrange themselves in a stable pentagon around the centre, six pins could not form a stable hexagon. Instead, one pin would move to the centre and the other five would form a pentagon around the centre pin, and this arrangement was stable. As he added more pins, they would arrange themselves in concentric rings around the centre.
The experiment functioned in two dimensions instead of three, but Thomson inferred the electrons in the atom arranged themselves in concentric shells and the could move within these shells but did not move from one shell to another them except when electrons were added or subtracted from the atom.
1906 Estimating electrons per atom
Before 1906 Thomson considered the atomic weight to be due to the mass of the electrons (which he continued to call "corpuscles"). Based on his own estimates of the electron mass, an atom would need tens of thousands electrons to account for the mass. In 1906 he used three different methods, X-ray scattering, beta ray absorption, or optical properties of gases, to estimate that "number of corpuscles is not greatly different from the atomic weight". This reduced the number of electrons to tens or at most a couple of hundred and that in turn meant that the positive sphere in Thomson's model contained most of the mass of the atom. This meant that Thomson's mechanical stability work from 1904 and the comparison to the periodic table were no longer valid. Moreover, the alpha particle, so important to the next advance in atomic theory by Rutherford, would no longer be viewed as an atom containing thousands of electrons.
In 1907, Thomson published The Corpuscular Theory of Matter which reviewed his ideas on the atom's structure and proposed further avenues of research.
In Chapter 6, he further elaborates his experiment using magnetised pins in water, providing an expanded table. For instance, if 59 pins were placed in the pool, they would arrange themselves in concentric rings of the order 20-16-13-8-2 (from outermost to innermost).
In Chapter 7, Thomson summarised his 1906 results on the number of electrons in an atom. He included one important correction: he replaced the beta-particle analysis with one based on the cathode ray experiments of August Becker, giving a result in better agreement with other approaches to the problem. Experiments by other scientists in this field had shown that atoms contain far fewer electrons than Thomson previously thought. Thomson now believed the number of electrons in an atom was a small multiple of its atomic weight: "the number of corpuscles in an atom of any element is proportional to the atomic weight of the element — it is a multiple, and not a large one, of the atomic weight of the element." This meant that almost all of the atom's mass had to be carried by the positive sphere, whatever it was made of.
Thomson in this book estimated that a hydrogen atom is 1,700 times heavier than an electron (the current measurement is 1,837). Thomson noted that no scientist had yet found a positively charged particle smaller than a hydrogen ion. He also wrote that the positive charge of an atom is a multiple of a basic unit of positive charge, equal to the negative charge of an electron. Thomson refused to jump to the conclusion that the basic unit of positive charge has a mass equal to that of the hydrogen ion, arguing that scientists first had to know how many electrons an atom contains. For all he could tell, a hydrogen ion might still contain a few electrons—perhaps two electrons and three units of positive charge.
1910 Multiple scattering
Thomson's difficulty with beta scattering in 1906 lead him to renewed interest in the topic. He encouraged J. Arnold Crowther to experiment with beta scattering through thin foils and, in 1910, Thomson produced a new theory of beta scattering. The two innovations in this paper was the introduction of scattering from the positive sphere of the atom and analysis that multiple or compound scattering was critical to the final results. This theory and Crowther's experimental results would be confronted by Rutherford's theory and Geiger and Mardsen new experiments with alpha particles.
Another innovation in Thomson's 1910 paper was that he modelled how an atom might deflect an incoming beta particle if the positive charge of the atom existed in discrete units of equal but arbitrary size, spread evenly throughout the atom, separated by empty space, with each unit having a positive charge equal to the electron's negative charge. Thomson therefore came close to deducing the existence of the proton, which was something Rutherford eventually did. In Rutherford's model of the atom, the protons are clustered in a very small nucleus, but in Thomson's alternative model, the positive units were spread throughout the atom.
Thomson's 1910 scattering model
In his 1910 paper "On the Scattering of rapidly moving Electrified Particles", Thomson presented equations that modelled how beta particles scatter in a collision with an atom. His work was based on beta scattering studies by James Crowther.
Deflection by the positive sphere
Thomson typically assumed the positive charge in the atom was uniformly distributed throughout its volume, encapsulating the electrons. In his 1910 paper, Thomson presented the following equation which isolated the effect of this positive sphere:
where k is the Coulomb constant, qe is the charge of the beta particle, qg is the charge of the positive sphere, m is the mass of the beta particle, and R is the radius of the sphere. Because the atom is many thousands of times heavier than the beta particle, no correction for recoil is needed.
Thomson did not explain how this equation was developed, but the historian John L. Heilbron provided an educated guess he called a "straight-line" approximation. Consider a beta particle passing through the positive sphere with its initial trajectory at a lateral distance b from the centre. The path is assumed to have a very small deflection and therefore is treated here as a straight line.

Inside a sphere of uniformly distributed positive charge the force exerted on the beta particle at any point along its path through the sphere would be directed along the radius r with magnitude:
The component of force perpendicular to the trajectory and thus deflecting the path of the particle would be:
The lateral change in momentum py is therefore
The resulting angular deflection, , is given by
where px is the average horizontal momentum taken to be equal to the incoming momentum. Since we already know the deflection is very small, we can treat as being equal to .
To find the average deflection angle , the angle for each value of b and the corresponding L are added across the face sphere, then divided by the cross-section area. per Pythagorean theorem.
This matches Thomson's formula in his 1910 paper.
Deflection by the electrons
Thomson modelled the collisions between a beta particle and the electrons of an atom by calculating the deflection of one collision then multiplying by a factor for the number of collisions as the particle crosses the atom.

For the electrons within an arbitrary distance s of the beta particle's path, their mean distance will be s/2. Therefore, the average deflection per electron will be
where qe is the elementary charge, k is the Coulomb constant, m and v are the mass and velocity of the beta particle.
The factor for the number of collisions was known to be the square root of the number of possible electrons along path. The number of electrons depends upon the density of electrons along the particle path times the path length L. The net deflection caused by all the electrons within this arbitrary cylinder of effect around the beta particle's path is
where N0 is the number of electrons per unit volume and is the volume of this cylinder.

Since Thomson calculated the deflection would be very small, he treats L as a straight line. Therefore where b is the distance of this chord from the centre. The mean of is given by the integral
We can now replace in the equation for to obtain the mean deflection :
where N is the number of electrons in the atom, equal to .
Deflection by the positive charge in discrete units
In his 1910 paper, Thomson proposed an alternative model in which the positive charge exists in discrete units separated by empty space, with those units being evenly distributed throughout the atom's volume.

In this concept, the average scattering angle of the beta particle is given by:
where σ is the ratio of the volume occupied by the positive charge to the volume of the whole atom. Thomson did not explain how he arrived at this equation.
Net deflection
To find the combined effect of the positive charge and the electrons on the beta particle's path, Thomson provided the following equation:
Demise of the plum pudding model
Main article: Rutherford scattering experiments
Left: Had Thomson's model been correct, all the alpha particles should have passed through the foil with minimal scattering.
Right: What Geiger and Marsden observed was that a small fraction of the alpha particles experienced strong deflection.
Thomson probed the structure of atoms through beta particle scattering, whereas his former student Ernest Rutherford was interested in alpha particle scattering. Beta particles are electrons emitted by radioactive decay, whereas alpha particles are essentially helium atoms, also emitted in process of decay. Alpha particles have considerably more momentum than beta particles and Rutherford found that matter scatters alpha particles in ways that Thomson's plum pudding model could not predict.
Between 1908 and 1913, Ernest Rutherford, Hans Geiger, and Ernest Marsden collaborated on a series of experiments in which they bombarded thin metal foils with a beam of alpha particles and measured the intensity versus scattering angle of the particles. They found that the metal foil could scatter alpha particles by more than 90°. This should not have been possible according to the Thomson model: the scattering into large angles should have been negligible. The odds of a beta particle being scattered by more than 90° under such circumstances is astronomically small, and since alpha particles typically have much more momentum than beta particles, their deflection should be smaller still. The Thomson models simply could not produce electrostatic forces of sufficient strength to cause such large deflection. The charges in the Thomson model were too diffuse. This led Rutherford to discard the Thomson for a new model where the positive charge of the atom is concentrated in a tiny nucleus.
Rutherford went on to make more compelling discoveries. In Thomson's model, the positive charge sphere was just an abstract component, but Rutherford found something concrete to attribute the positive charge to: particles he dubbed "protons". Whereas Thomson believed that the electron count was roughly correlated to the atomic weight, Rutherford showed that (in a neutral atom) it is exactly equal to the atomic number.
Thomson hypothesised that the arrangement of the electrons in the atom somehow determined the spectral lines of a chemical element. He was on the right track, but it had nothing to do with how atoms circulated in a sphere of positive charge. Scientists eventually discovered that it had to do with how electrons absorb and release energy in discrete quantities, moving through energy levels which correspond to emission and absorption spectra. Thomson had not incorporated quantum mechanics into his atomic model, which at the time was a very new field of physics. Niels Bohr and Erwin Schroedinger later incorporated quantum mechanics into the atomic model.
Rutherford's nuclear model
Main articles: Rutherford model and Bohr modelRutherford's 1911 paper on alpha particle scattering showed that Thomson's scattering model could not explain the large angle scattering and it showed that multiple scattering was not necessary to explain the data. However, in the years immediately following its publication few scientists took note. The scattering model predictions were not considered definitive evidence against Thomson's plum pudding model. Thomson and Rutherford had pioneered scattering as a technique to probe atoms, its reliability and value were unproven. Before Rutherford's paper the alpha particle was considered an atom, not a compact mass. It was not clear why it should be a good probe. Moreover, Rutherford's paper did not discuss the atomic electrons vital to practical problems like chemistry or atomic spectroscopy. Rutherford's nuclear model would only become widely accepted after the work of Niels Bohr.
Mathematical Thomson problem
The Thomson problem in mathematics seeks the optimal distribution of equal point charges on the surface of a sphere. Unlike the original Thomson atomic model, the sphere in this purely mathematical model does not have a charge, and this causes all the point charges to move to the surface of the sphere by their mutual repulsion. There is still no general solution to Thomson's original problem of how electrons arrange themselves within a sphere of positive charge.
Origin of the nickname

The first known writer to compare Thomson's model to a plum pudding was an anonymous reporter in an article for the British pharmaceutical magazine The Chemist and Druggist in August 1906.
While the negative electricity is concentrated on the extremely small corpuscle, the positive electricity is distributed throughout a considerable volume. An atom would thus consist of minute specks, the negative corpuscles, swimming about in a sphere of positive electrification, like raisins in a parsimonious plum-pudding, units of negative electricity being attracted toward the centre, while at the same time repelling each other.
The analogy was never used by Thomson nor his colleagues. It seems to have been a conceit of popular science writers to make the model easier to understand for the layman.
References
- Thomson 1907, p. 103 "In default of exact knowledge of the nature of the way in which positive electricity occurs in the atom, we shall consider a case in which the positive electricity is distributed in the way most amenable to mathematical calculation, i.e., when it occurs as a sphere of uniform density, throughout which the corpuscles are distributed."
- ^ Giora Hon; Bernard R. Goldstein (6 September 2013). "J. J. Thomson's plum-pudding atomic model: The making of a scientific myth". Annalen der Physik. 525 (8–9): A129 – A133. Bibcode:2013AnP...525A.129H. doi:10.1002/andp.201300732.
- Letter from J. J. Thomson to Oliver Lodge dated 11 April 1904, quoted in Davis & Falconer 1997, p. 153:
"With regard to positive electrification I have been in the habit of using the crude analogy of a liquid with a certain amount of cohesion, enough to keep it from flying to bits under its own repulsion. I have however always tried to keep the physical conception of the positive electricity in the background because I have always had hopes (not yet realised) of being able to do without positive electrification as a separate entity and to replace it by some property of the corpuscles."
- ^ Pais, Abraham (2002). Inward bound: of matter and forces in the physical world (Reprint ed.). Oxford: Clarendon Press ISBN 978-0-19-851997-3.
- Thomson, William (1869). "On Vortex Atoms". Proceedings of the Royal Society of Edinburgh. 6: 94–105. doi:10.1017/S0370164600045430.
- Kragh, Helge (2002). Quantum Generations: A History of Physics in the Twentieth Century (Reprint ed.). Princeton University Press. pp. 43–45. ISBN 978-0691095523.
- O'Hara, J. G. (March 1975). "George Johnstone Stoney, F.R.S., and the Concept of the Electron". Notes and Records of the Royal Society of London. 29 (2): 265–276. doi:10.1098/rsnr.1975.0018. JSTOR 531468. S2CID 145353314.
- ^ Whittaker, E. T. (1989). A history of the theories of aether & electricity. New York: Dover Publications. ISBN 978-0-486-26126-3.
- ^ Helge Kragh (Oct. 2010). Before Bohr: Theories of atomic structure 1850-1913. RePoSS: Research Publications on Science Studies 10. Aarhus: Centre for Science Studies, University of Aarhus.
- ^ Fowler, Michael. "Models of the Atom". University of Virginia.
- Thomson 1897.
- Falconer, Isobel (July 1987). "Corpuscles, Electrons and Cathode Rays: J.J. Thomson and the 'Discovery of the Electron'". The British Journal for the History of Science. 20 (3): 241–276. doi:10.1017/S0007087400023955. ISSN 0007-0874.
- J. J. Thomson (1899). "On the Masses of the Ions in Gases at Low Pressures". Philosophical Magazine. 5. 48 (295): 547–567.
"...the magnitude of this negative charge is about 6 × 10 electrostatic units, and is equal to the positive charge carried by the hydrogen atom in the electrolysis of solutions. In gases at low pressures these units of negative electric charge are always associated with carriers of a definite mass. This mass is exceedingly small, being only about 1.4 × 10 of that of the hydrogen ion, the smallest mass hitherto recognized as capable of a separate existence. The production of negative electrification thus involves the splitting up of an atom, as from a collection of atoms something is detached whose mass is less than that of a single atom." - ^ Thomson 1904.
- Kumar, Manjit (2008). Quantum Einstein, Bohr and the Great Debate. W. W. Norton. ISBN 978-0393339888.
- Kragh, Helge (2001). "The first subatomic explanations of the periodic system". Foundations of Chemistry. 3 (2): 129–143. doi:10.1023/A:1011448410646.
- Thomson 1904: "We suppose that the mass of an atom is the sum of the masses of the corpuscles it contains, so that the atomic weight of an element is measured by the number of corpuscles in its atom."
- Baily, C. (January 2013). "Early atomic models – from mechanical to quantum (1904–1913)". The European Physical Journal H. 38 (1): 1–38. arXiv:1208.5262. Bibcode:2013EPJH...38....1B. doi:10.1140/epjh/e2012-30009-7. ISSN 2102-6459.
- Thomson, J. J. (10 March 1905), The Structure of the Atom (PDF). Reprinted in Davis & Falconer 1997
- Thomson, J.J. (June 1906). "LXX. On the number of corpuscles in an atom". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 11 (66): 769–781. doi:10.1080/14786440609463496. ISSN 1941-5982.
- ^ John L. Heilbron (1968). "The Scattering of α and β Particles and Rutherford's Atom". Archive for History of Exact Sciences. 4 (4): 247–307. doi:10.1007/BF00411591. ISSN 0003-9519. JSTOR 41133273.
- Thomson 1907.
- Thomson 1907, p. 27
- Thomson 1907, p. 162: "Since the mass of a corpuscle is only about one-seventeen-hundredth part of that of an atom of hydrogen, it follows that if there are only a few corpuscles in the hydrogen atom the mass of the atom must in the main be due to its other constituent — the positive electricity."
- Thomson 1907, pp. 23, 26.
- J. J. Thomson (1907). The Corpuscular Theory of Matter. p. 26-27: "In an unelectrified atom there are as many units of positive electricity as there are of negative; an atom with a unit of positive charge is a neutral atom which has lost one corpuscle, while an atom with a unit of negative charge is a neutral atom to which an additional corpuscle has been attached."
- Thomson (1907), p. 27: "No positively electrified body has yet been found with a mass less than that of a hydrogen atom. We cannot, however, without further investigation infer from this that the mass of the unit of charge of positive electricity is equal to the mass of the hydrogen atom, for all we know about the electrified system is, that the positive electricity is in excess by one unit over the negative electricity; any system containing n units of positive electricity and (n-1) corpuscles would satisfy this condition whatever might be the value of n. Before we can deduce any conclusions as to the mass of the unit of positive electricity we must know something about the number of corpuscles in the system."
- Crowther, J. A. (1910-09-15). "On the scattering of Homogeneous β-Rays and the number of Electrons in the Atom". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. 84 (570): 226–247. Bibcode:1910RSPSA..84..226C. doi:10.1098/rspa.1910.0074. ISSN 0950-1207.
- Thomson, Joseph J. "On the scattering of rapidly moving electrified particles". Cambridge Philosophical Society, 1910.
- Thomson (1910): "The amount of deflection due to (2) will depend upon whether the positive electricity is uniformly distributed through the atom, or whether it is supposed to be divided into equal units, each occupying a finite volume probably much greater than the volume occupied by a corpuscle."
- ^ J. J. Thomson (1910). "On the Scattering of rapidly moving Electrified Particles". Proceedings of the Cambridge Philosophical Society. 15: 465–471.
- Heilbron (1968). p. 278
- "Electric Field, Spherical Geometry".
- Beiser (1969). Perspectives of Modern Physics, p. 109
- Belyaev, Alexander; Ross, Douglas (2021). The Basics of Nuclear and Particle Physics. Undergraduate Texts in Physics. Cham: Springer International Publishing. Bibcode:2021bnpp.book.....B. doi:10.1007/978-3-030-80116-8. ISBN 978-3-030-80115-1.
- Rutherford (1911): "This scattering is far more marked for the β than for the α particle on account of the much smaller momentum and energy of the former particle."
- Levin, Y.; Arenzon, J. J. (2003). "Why charges go to the Surface: A generalized Thomson Problem". Europhys. Lett. 63 (3): 415–418. arXiv:cond-mat/0302524. Bibcode:2003EL.....63..415L. doi:10.1209/epl/i2003-00546-1. S2CID 250764497.
- Roth, J. (2007-10-24). "Description of a highly symmetric polytope observed in Thomson's problem of charges on a hypersphere". Physical Review E. 76 (4): 047702. Bibcode:2007PhRvE..76d7702R. doi:10.1103/PhysRevE.76.047702. ISSN 1539-3755. PMID 17995142.
Although Thomson's model has been outdated for a long time by quantum mechanics, his problem of placing charges on a sphere is still noteworthy.
- "What is Matter?". The Chemist and Druggist. 69 (8): 329–330. 25 August 1906.
Bibliography
- Davis, E. A.; Falconer, I. J. (1997). J. J. Thomson and the Discovery of the Electron. Taylor & Francis. ISBN 0-203-79233-5.
- Thomson, J. J. (1897). "Cathode rays" (PDF). Philosophical Magazine. 44 (269): 293–316. doi:10.1080/14786449708621070.
- Thomson, J. J. (1899). "On the Masses of the Ions in Gases at Low Pressures". Philosophical Magazine. 5. 48 (295): 547–567.
- Thomson, J. J. (March 1904). "On the Structure of the Atom: an Investigation of the Stability and Periods of Oscillation of a number of Corpuscles arranged at equal intervals around the Circumference of a Circle; with Application of the Results to the Theory of Atomic Structure". Philosophical Magazine. Sixth series. 7 (39): 237–265. doi:10.1080/14786440409463107. Archived (PDF) from the original on 2022-10-09.
- Thomson, J. J. (1907). The Corpuscular Theory of Matter. Charles Scribner's Sons.
- Ernest Rutherford (1911). "The Scattering of α and β Particles by Matter and the Structure of the Atom" (PDF). Philosophical Magazine. Series 6. 21 (125): 669–688. doi:10.1080/14786440508637080.
- J. J. Thomson (1906). "On the Number of Corpuscles in an Atom" (PDF). Philosophical Magazine. 6. 11 (66): 769–781. doi:10.1080/14786440609463496.
- J. J. Thomson (1910). "On the Scattering of rapidly moving Electrified Particles". Proceedings of the Cambridge Philosophical Society. 15: 465–471.
| Atomic models | |
|---|---|
| Historic models |
|
| Current models |
|




 , is given by
, is given by

 as being equal to
as being equal to  , the angle for each value of b and the corresponding L are added across the face sphere, then divided by the cross-section area.
, the angle for each value of b and the corresponding L are added across the face sphere, then divided by the cross-section area.  per
per 



 is the volume of this cylinder.
is the volume of this cylinder.
 is given by the integral
is given by the integral

 to obtain the mean deflection
to obtain the mean deflection  :
:


 .
.

