The distance (or perpendicular distance) from a point to a line is the shortest distance from a fixed point to any point on a fixed infinite line in Euclidean geometry. It is the length of the line segment which joins the point to the line and is perpendicular to the line. The formula for calculating it can be derived and expressed in several ways.
Knowing the shortest distance from a point to a line can be useful in various situations—for example, finding the shortest distance to reach a road, quantifying the scatter on a graph, etc. In Deming regression, a type of linear curve fitting, if the dependent and independent variables have equal variance this results in orthogonal regression in which the degree of imperfection of the fit is measured for each data point as the perpendicular distance of the point from the regression line.
Cartesian coordinates
Line defined by an equation
In the case of a line in the plane given by the equation ax + by + c = 0, where a, b and c are real constants with a and b not both zero, the distance from the line to a point (x0,y0) is
The point on this line which is closest to (x0,y0) has coordinates:
Horizontal and vertical lines
In the general equation of a line, ax + by + c = 0, a and b cannot both be zero unless c is also zero, in which case the equation does not define a line. If a = 0 and b ≠ 0, the line is horizontal and has equation y = -c/b. The distance from (x0, y0) to this line is measured along a vertical line segment of length |y0 - (-c/b)| = |by0 + c| / |b| in accordance with the formula. Similarly, for vertical lines (b = 0) the distance between the same point and the line is |ax0 + c| / |a|, as measured along a horizontal line segment.
Line defined by two points
If the line passes through two points P1=(x1,y1) and P2=(x2,y2) then the distance of (x0,y0) from the line is:
The denominator of this expression is the distance between P1 and P2. The numerator is twice the area of the triangle with its vertices at the three points, (x0,y0), P1 and P2. See: Area of a triangle § Using coordinates. The expression is equivalent to , which can be obtained by rearranging the standard formula for the area of a triangle: , where b is the length of a side, and h is the perpendicular height from the opposite vertex.
Line defined by point and angle
If the line passes through the point P = (Px, Py) with angle θ, then the distance of some point (x0, y0) to the line is
Proofs
An algebraic proof
This proof is valid only if the line is neither vertical nor horizontal, that is, we assume that neither a nor b in the equation of the line is zero.
The line with equation ax + by + c = 0 has slope -a/b, so any line perpendicular to it will have slope b/a (the negative reciprocal). Let (m, n) be the point of intersection of the line ax + by + c = 0 and the line perpendicular to it which passes through the point (x0, y0). The line through these two points is perpendicular to the original line, so
Thus, and by squaring this equation we obtain:
Now consider,
using the above squared equation. But we also have,
since (m, n) is on ax + by + c = 0. Thus,
and we obtain the length of the line segment determined by these two points,
A geometric proof

This proof is valid only if the line is not horizontal or vertical.
Drop a perpendicular from the point P with coordinates (x0, y0) to the line with equation Ax + By + C = 0. Label the foot of the perpendicular R. Draw the vertical line through P and label its intersection with the given line S. At any point T on the line, draw a right triangle TVU whose sides are horizontal and vertical line segments with hypotenuse TU on the given line and horizontal side of length |B| (see diagram). The vertical side of ∆TVU will have length |A| since the line has slope -A/B.
∆PRS and ∆TVU are similar triangles, since they are both right triangles and ∠PSR ≅ ∠TUV since they are corresponding angles of a transversal to the parallel lines PS and UV (both are vertical lines). Corresponding sides of these triangles are in the same ratio, so:
If point S has coordinates (x0,m) then |PS| = |y0 - m| and the distance from P to the line is:
Since S is on the line, we can find the value of m,
and finally obtain:
A variation of this proof is to place V at P and compute the area of the triangle ∆UVT two ways to obtain that where D is the altitude of ∆UVT drawn to the hypoteneuse of ∆UVT from P. The distance formula can then used to express , , and in terms of the coordinates of P and the coefficients of the equation of the line to get the indicated formula.
A vector projection proof
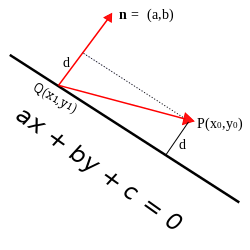
Let P be the point with coordinates (x0, y0) and let the given line have equation ax + by + c = 0. Also, let Q = (x1, y1) be any point on this line and n the vector (a, b) starting at point Q. The vector n is perpendicular to the line, and the distance d from point P to the line is equal to the length of the orthogonal projection of on n. The length of this projection is given by:
Now,
- so and
thus
Since Q is a point on the line, , and so,
Another formula
It is possible to produce another expression to find the shortest distance of a point to a line. This derivation also requires that the line is not vertical or horizontal.
The point P is given with coordinates (). The equation of a line is given by . The equation of the normal of that line which passes through the point P is given .
The point at which these two lines intersect is the closest point on the original line to the point P. Hence:
We can solve this equation for x,
The y coordinate of the point of intersection can be found by substituting this value of x into the equation of the original line,
Using the equation for finding the distance between 2 points, , we can deduce that the formula to find the shortest distance between a line and a point is the following:
Recalling that m = -a/b and k = - c/b for the line with equation ax + by + c = 0, a little algebraic simplification reduces this to the standard expression.
Vector formulation

The equation of a line can be given in vector form:
Here a is the position of a point on the line, and n is a unit vector in the direction of the line. Then as scalar t varies, x gives the locus of the line.
The distance of an arbitrary point p to this line is given by
This formula can be derived as follows: is a vector from p to the point a on the line. Then is the projected length onto the line and so
is a vector that is the projection of onto the line. Thus
is the component of perpendicular to the line. The distance from the point to the line is then just the norm of that vector. This more general formula is not restricted to two dimensions.
Another vector formulation
If the line (l ) goes through point A and has a direction vector , the distance between point P and line (l) is
where is the cross product of the vectors and and where is the vector norm of .
Note that cross products only exist in dimensions 3 and 7 and trivially in dimensions 0 and 1 (where the cross product is constant 0).
See also
- Hesse normal form
- Line-line intersection
- Distance between two lines
- Distance from a point to a plane
- Skew lines#Distance
Notes
- Larson & Hostetler 2007, p. 452
- Spain 2007
- Larson & Hostetler 2007, p. 522
- Between Certainty and Uncertainty: Statistics and Probability in Five Units With Notes on Historical Origins and Illustrative Numerical Examples
- Ballantine & Jerbert 1952 do not mention this restriction in their article
- If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.
- Ballantine & Jerbert 1952
- Anton 1994, pp. 138-9
- Larson & Hostetler 2007, p. 522
- Sunday, Dan. "Lines and Distance of a Point to a Line". softSurfer. Retrieved 6 December 2013.
References
- Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7
- Ballantine, J.P.; Jerbert, A.R. (1952), "Distance from a line or plane to a point", American Mathematical Monthly, 59: 242–243, doi:10.2307/2306514
- Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 0-618-62719-7
- Spain, Barry (2007) , Analytical Conics, Dover Publications, ISBN 0-486-45773-7
Further reading
- Deza, Michel Marie; Deza, Elena (2013), Encyclopedia of Distances (2nd ed.), Springer, p. 86, ISBN 9783642309588



 , which can be obtained by rearranging the standard formula for the area of a triangle:
, which can be obtained by rearranging the standard formula for the area of a triangle:  , where b is the length of a side, and h is the perpendicular height from the opposite vertex.
, where b is the length of a side, and h is the perpendicular height from the opposite vertex.


 and by squaring this equation we obtain:
and by squaring this equation we obtain:









 where D is the altitude of ∆UVT drawn to the hypoteneuse of ∆UVT from P. The distance formula can then used to express
where D is the altitude of ∆UVT drawn to the hypoteneuse of ∆UVT from P. The distance formula can then used to express  ,
,  , and
, and  in terms of the coordinates of P and the coefficients of the equation of the line to get the indicated formula.
in terms of the coordinates of P and the coefficients of the equation of the line to get the indicated formula.
 on n. The length of this projection is given by:
on n. The length of this projection is given by:

 so
so  and
and 

 , and so,
, and so,

 ).
The equation of a line is given by
).
The equation of a line is given by  . The equation of the normal of that line which passes through the point P is given
. The equation of the normal of that line which passes through the point P is given  .
.



 , we can deduce that the formula to find the shortest distance between a line and a point is the following:
, we can deduce that the formula to find the shortest distance between a line and a point is the following:



 is a vector from p to the point a on the line. Then
is a vector from p to the point a on the line. Then  is the projected length onto the line and so
is the projected length onto the line and so


 , the distance between point P and line (l) is
, the distance between point P and line (l) is

 is the
is the  and
and  is the vector norm of
is the vector norm of 