| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Polarimeter" – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) |

1. Light source
2. Unpolarized light
3. Linear polarizer
4. Linearly polarized light
5. Sample tube containing chiral molecules under study
6. Optical rotation due to molecules
7. Rotatable linear analyzer
8. Detector
A polarimeter is a scientific instrument used to measure optical rotation: the angle of rotation caused by passing linearly polarized light through an optically active substance.
Some chemical substances are optically active, and linearly polarized (uni-directional) light will rotate either to the left (counter-clockwise) or right (clockwise) when passed through these substances. The amount by which the light is rotated is known as the angle of rotation. The direction (clockwise or counterclockwise) and magnitude of the rotation reveals information about the sample's chiral properties such as the relative concentration of enantiomers present in the sample.
History
See also: Optical rotation § HistoryPolarization by reflection was discovered in 1808 by Étienne-Louis Malus (1775–1812).
Measuring principle
The ratio, the purity, and the concentration of two enantiomers can be measured via polarimetry. Enantiomers are characterized by their property to rotate the plane of linear polarized light. Therefore, those compounds are called optically active and their property is referred to as optical rotation. Light sources such as a light bulb, Tungsten Halogen, or the sun emit electromagnetic waves at the frequency of visible light. Their electric field oscillates in all possible planes relative to their direction of propagation. In contrast to that, the waves of linear-polarized light oscillate in parallel planes.
If light encounters a polarizer, only the part of the light that oscillates in the defined plane of the polarizer may pass through. That plane is called the plane of polarization. The plane of polarization is turned by optically active compounds. According to the direction in which the light is rotated, the enantiomer is referred to as dextro-rotatory or levo-rotatory.
The optical activity of enantiomers is additive. If different enantiomers exist together in one solution, their optical activity adds up. That is why racemates are optically inactive, as they nullify their clockwise and counter clockwise optical activities. The optical rotation is proportional to the concentration of the optically active substances in solution. Polarimeters may therefore be applied for concentration measurements of enantiomer-pure samples. With a known concentration of a sample, polarimeters may also be applied to determine the specific rotation when characterizing a new substance. The specific rotation is a physical property and defined as the optical rotation α at a path length l of 1 dm, a concentration c of 10 g/L, a temperature T (usually 20 °C) and a light wavelength λ (usually sodium D line at 589.3 nm):
This tells us how much the plane of polarization is rotated when the ray of light passes through a specific amount of optically active molecules of a sample. Therefore, the optical rotation depends on temperature, concentration, wavelength, path length, and the substancebeing analyzed.
Construction
The polarimeter is made up of two Nicol prisms (the polarizer and analyzer). The polarizer is fixed and the analyzer can be rotated. The prisms may be thought of as slits S1 and S2. The light waves may be considered to correspond to waves in the string. The polarizer S1 allows only those light waves which move in a single plane. This causes the light to become plane polarized. When the analyzer is also placed in a similar position it allows the light waves coming from the polarizer to pass through it. When it is rotated through the right angle no waves can pass through the right angle and the field appears to be dark. If now a glass tube containing an optically active solution is placed between the polarizer and analyzer the light now rotates through the plane of polarization through a certain angle, the analyzer will have to be rotated in same angle.
Operation
Polarimeters measure this by passing monochromatic light through the first of two polarising plates, creating a polarized beam. This first plate is known as the polarizer. This beam is then rotated as it passes through the sample. After passing through the sample, a second polarizer, known as the analyzer, rotates either via manual rotation or automatic detection of the angle. When the analyzer is rotated such that all the light or no light can pass through, then one can find the angle of rotation which is equal to the angle θ by which the analyser was rotated in the former case, or 90-θ in the latter case.
Types of polarimeter
Laurent's half-shade polarimeter
When plane-polarised light passes through some crystals, the velocity of left-polarized light is different from that of the right-polarized light, thus the crystals are said to have two refractive indices, i.e. double refracting.
Construction: The polarimeter consists of a monochromatic source S which is placed at focal point of a convex lens L. Just after the convex lens there is a Nicol Prism P which acts as a polariser. H is a half shade device which divides the field of polarized light emerging out of the Nicol P into two halves, generally of unequal brightness. T is a glass tube in which an optically active solution is filled. The light, after passing through T, is allowed to fall on the analyzing Nicol A which can be rotated about the axis of the tube. The rotation of the analyzer can be measured with the help of a scale C.
Working principle: To understand the need of a half-shade device, let us suppose that it is not present. The position of the analyzer is adjusted so that the field of view is dark when the tube is empty. The position of the analyzer is noted on the circular scale. Now the tube is filled with the optically active solution and it is set in its proper position. The optically active solution rotates the plane of polarization of the light emerging out of the polarizer P by some angle, so the light is transmitted by analyzer A and the field of view of the telescope becomes bright. Now the analyzer is rotated by a finite angle so that the field of view of the telescope again becomes dark. This will happen only when the analyzer is rotated by the same angle by which the plane of polarization of light is rotated by the optically active solution.
The position of the analyzer is again noted. The difference of the two readings will give the angle of rotation of the plane of polarization.
A difficulty faced in the above procedure is that when analyzer is rotated for the total darkness, then it is attained gradually and hence it is difficult to find the exact position correctly for which complete darkness is obtained. To overcome the above difficulty, the half-shade device is introduced between polarizer P and the glass tube T.
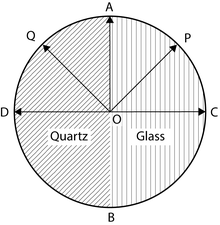
Half shade device: It consist of two semicircular plates ACB and ADB. One half ACB is made of glass while other half is made of quartz. Both halves are cemented together. The quartz is cut parallel to the optic axis. Thickness of the quartz is selected in such a way that it introduces a path difference of ’A/2 between ordinary and extraordinary ray. The thickness of the glass is selected in such a way that it absorbs the same amount of light as is absorbed by the quartz half.
Consider that the vibration of polarization is along OP. On passing through the glass half the vibrations remain along OP. But on passing through the quartz half these vibrations will split into 0- and £-components. The £-components are parallel to the optic axis while O- component is perpendicular to optic axis. The O-component travels faster in quartz and hence an emergence 0-component will be along OD instead of along OC. Thus components OA and OD will combine to form a resultant vibration along OQ which makes the same angle with optic axis as OP. Now if the Principal plane of the analyzing Nicol is parallel to OP then the light will pass through the glass half unobstructed. Hence the glass half will be brighter than the quartz half or we can say that the glass half will be bright and the quartz half will be dark. Similarly if the principal plane of the analyzing Nicol is parallel to OQ then the quartz half will be bright and the glass half will be dark.
When the principal plane of the analyzer is along AOB then both halves will be equally bright. On the other hand, if the principal plane of the analyzer is along DOC then both the halves will be equally dark.
Thus it is clear that if the analyzing Nicol is slightly disturbed from DOC then one half becomes brighter than the other. Hence by using the half shade device, one can measure the angle of rotation more accurately.
Determination of specific rotation: In order to determine a specific rotation of an optically active substance (say, sugar), the polarimeter tube is first filled with pure water and the analyzer is adjusted for equal darkness (both the halves should be equally dark) point. The position of the analyzer is noted with the help of the scale. Now the polarimeter tube is filled with a sugar solution of known concentration and again the analyzer is adjusted in such a way that again the equally dark point is achieved. The position of the analyzer is again noted. The difference of the two readings will give the angle of rotation θ. Hence, a specific rotation S is determined as S = θ/LC, where L is the optical path length and C is concentration of the substance.
Biquartz polarimeter
A biquartz polarimeter uses a biquartz plate, consisting of two semicircular plates of quartz, each of thickness 3.75mm. One half consists of right-handed optically active quartz, while the other is left-handed optically active quartz.
Manual
The earliest polarimeters, which date back to the 1830s, required the user to physically rotate one polarizing element (the analyzer) whilst viewing through another static element (the detector). The detector was positioned at the opposite end of a tube containing the optically active sample, and the user used his/her eye to judge the "alignment" when least light was observed. The angle of rotation was then read from a simple fixed to the moving polariser to within a degree or so.
Although most manual polarimeters produced today still adopt this basic principle, the many developments applied to the original opto-mechanical design over the years have significantly improved measurement performance. The introduction of a half-wave plate increased "distinction sensitivity", whilst a precision glass scale with vernier drum facilitated the final reading to within ca. ±0.05º. Most modern manual polarimeters also incorporate a long-life yellow LED in place of the more costly sodium arc lamp as a light source.
Semi-automatic
Today, semi-automatic polarimeters are available. The operator views the image via a digital display adjusts the analyzer angle with electronic controls.
Fully automatic

Fully automatic polarimeters are now widely used and simply require the user to press a button and wait for a digital readout. Fast automatic digital polarimeters yield an accurate result within a few seconds, regardless of the rotation angle of the sample. In addition, they provide continuous measurement, facilitating High-performance liquid chromatography and other kinetic investigations.
Another feature of modern polarimeters is the Faraday modulator. The Faraday modulator creates an alternating current magnetic field. It oscillates the plane of polarization to enhance the detection accuracy by allowing the point of maximal darkness to be passed through again and again and thus be determined with even more accuracy.
As the temperature of the sample has a significant influence on the optical rotation of the sample, modern polarimeters have already included Peltier elements to actively control the temperature. Special techniques as temperature controlled sample tubes reduce measuring errors and ease operation. Results can directly be transferred to computers or networks for automatic processing. Traditionally, accurate filling of the sample cell had to be checked outside the instrument, as an appropriate control from within the device was not possible. Nowadays a camera system can help to monitor the sample and accurate filling conditions in the sample cell. Furthermore, features for automatic filling introduced by few companies are available on the market. When working with caustic chemicals, acids, and bases it can be beneficial to not load the polarimeter cell by hand. Both of these options help to avoid potential errors caused by bubbles or particles.
Sources of error
The angle of rotation of an optically active substance can be affected by:
- Concentration of the sample
- Wavelength of light passing through the sample (generally, angle of rotation and wavelength tend to be inversely proportional)
- Temperature of the sample (generally the two are directly proportional)
- Length of the sample cell (input by the user into most automatic polarimeters to ensure better accuracy)
- Filling conditions (bubbles, temperature and concentration gradients)
Most modern polarimeters have methods for compensating or/and controlling these errors.
Calibration
Traditionally, a sucrose solution with a defined concentration was used to calibrate polarimeters relating the amount of sugar molecules to the light polarization rotation. The International Commission for Uniform Methods of Sugar Analysis (ICUMSA) played a key role in unifying analytical methods for the sugar industry, set standards for the International Sugar Scale (ISS) and the specifications for polarimeters in sugar industry. However, sugar solutions are prone to contamination and evaporation. Moreover, the optical rotation of a substance is very sensitive to temperature. A more reliable and stable standard was found: crystalline quartz which is oriented and cut in a way that it matches the optical rotation of a normal sugar solution, but without showing the disadvantages mentioned above. Quartz (silicon dioxide, SiO2) is a common mineral, a trigonal chemical compound of silicon and oxygen. Nowadays, quartz plates or quartz control plates of different thickness serve as standards to calibrate polarimeters and saccharimeters. In order to ensure reliable and comparable results, quartz plates can be calibrated and certified by metrology institutes. However,. Alternatively, calibration may be checked using a Polarization Reference Standard, which consists of a plate of quartz mounted in a holder perpendicular to the light path. These standards are available, traceable to NIST, by contacting Rudolph Research Analytical, located at 55 Newburgh Road, Hackettstown, NJ 07840, USA. A calibration first consists of a preliminary test in which the fundamental calibration capability is checked. The quartz control plates must meet the required minimum requirements with respect to their dimensions, optical pureness, flatness, parallelism of the faces and optical axis errors. After that, the actual measurement value - the optical rotation - is measured with the precision polarimeter. The measurement uncertainty of the polarimeter amounts to 0.001° (k=2).
Applications
Because many optically active chemicals such as tartaric acid, are stereoisomers, a polarimeter can be used to identify which isomer is present in a sample – if it rotates polarized light to the left, it is a levo-isomer, and to the right, a dextro-isomer. It can also be used to measure the ratio of enantiomers in solutions.
The optical rotation is proportional to the concentration of the optically active substances in solution. Polarimetry may therefore be applied for concentration measurements of enantiomer-pure samples. With a known concentration of a sample, polarimetry may also be applied to determine the specific rotation (a physical property) when characterizing a new substance.
Chemical industry
Many chemicals exhibit a specific rotation as a unique property (an intensive property like refractive index or Specific gravity) which can be used to distinguish it. Polarimeters can identify unknown samples based on this if other variables such as concentration and length of sample cell length are controlled or at least known. This is used in the chemical industry.
By the same token, if the specific rotation of a sample is already known, then the concentration and/or purity of a solution containing it can be calculated.
Most automatic polarimeters make this calculation automatically, given input on variables from the user.
Food, beverage and pharmaceutical industries
Concentration and purity measurements are especially important to determine product or ingredient quality in the food & beverage and pharmaceutical industries. Samples that display specific rotations that can be calculated for purity with a polarimeter include:
- Steroids
- Diuretics
- Antibiotics
- Narcotics
- Vitamins
- Analgesics
- Amino acids
- Essential oils
- Polymers
- Starches
- Sugars
Polarimeters are used in the sugar industry for determining quality of both juice from sugar cane and the refined sucrose. Often, the sugar refineries use a modified polarimeter with a flow cell (and used in conjunction with a refractometer) called a saccharimeter. These instruments use the International Sugar Scale, as defined by the International Commission for Uniform Methods of Sugar Analysis (ICUMSA).
See also
References
- "Polarimeter | WordNet Search". wordnetweb.princeton.edu. Retrieved 2023-04-27.
- ^ "Polarimeter". physics.kenyon.edu. Archived from the original on 2023-05-13. Retrieved 2023-04-27.
- Hart, C. (2002), Organische Chemie, Wiley-VCH, ISBN 3-527-30379-0
- Carey, F. A.; R. J. Sundberg (2007). Advanced Organic Chemistry, Part A: Structure and Mechanisms (Fifth ed.). Springer. p. 123. doi:10.1007/978-0-387-44899-2. ISBN 978-0-387-44897-8.
- "Group :: Anton-Paar.com". Anton Paar.
- Polarimetry Archived 2011-09-27 at the Wayback Machine. chem.vt.edu
- ICUMSA Specification and Standard SPS-1 (1998)
- Schulz, M. (2006). High-accuracy polarimetric calibration of Quartz Control Plates (PDF). Rio de Janeiro, Brazil: XVIII IMEKO WORLD CONGRESS Metrology for a Sustainable Development.
- Chandrasekhar, S. (1953). "Theoretical interpretation of the optical activity of quartz". Proceedings of the Indian Academy of Sciences, Section A. 37 (3): 468. doi:10.1007/BF03052667. S2CID 93769450.
- "Polarimetric saccharimeters graduated in accordance with the ICUMSA, International Sugar Scale" (PDF). OIML R. 14. International Organization of Legal Metrology: 4. 1995.
- "Polarimetric calibration of quartz control plates". 2 October 2020.
 is a physical property and defined as the optical rotation α at a path length l of 1 dm, a concentration c of 10 g/L, a temperature T (usually 20 °C) and a light wavelength λ (usually sodium D line at 589.3 nm):
is a physical property and defined as the optical rotation α at a path length l of 1 dm, a concentration c of 10 g/L, a temperature T (usually 20 °C) and a light wavelength λ (usually sodium D line at 589.3 nm):
