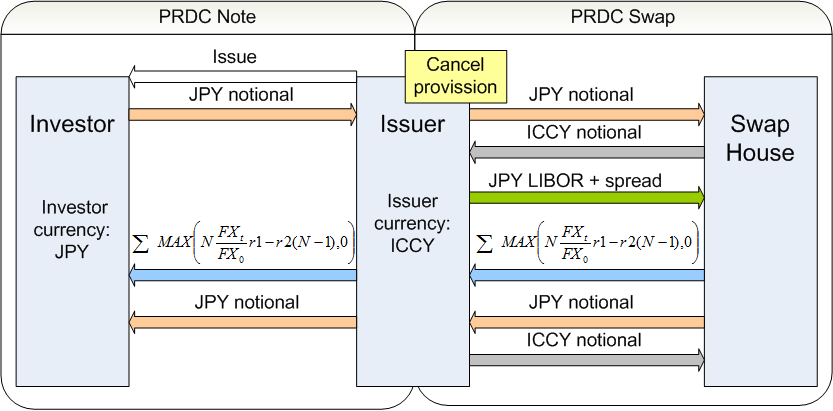
A dual-currency note (DC) pays coupons in the investor's domestic currency with the notional in the issuer's domestic currency. A reverse dual-currency note (RDC) is a note which pays a foreign interest rate in the investor's domestic currency. A power reverse dual-currency note (PRDC) is a structured product where an investor is seeking a better return and a borrower a lower rate by taking advantage of the interest rate differential between two economies. The power component of the name denotes higher initial coupons and the fact that coupons rise as the foreign exchange rate depreciates. The power feature comes with a higher risk for the investor, which characterizes the product as leveraged carry trade. Cash flows may have a digital cap feature where the rate gets locked once it reaches a certain threshold. Other add-on features include barriers such as knockouts and cancel provision for the issuer. PRDCs are part of the wider Structured Notes Market.
Market
The majority of investors are Japanese with US$9 billion worth of notes issued in 2003 and the issued notional increasing every year thereafter up until 2008 when it sharply declined. Major participants in the market include issuers (usually Supranationals) of the notes under their Euro Medium Term Note program. Also heavily involved are PRDC swap hedgers – the major ones include JPMorgan Chase, Nomura Securities Co., UBS Investment Bank, Deutsche Bank, Goldman Sachs, Citigroup, Barclays Investment Bank, Credit Suisse, and Bank of America Merrill Lynch.
Payoff and cashflows
The investor pays a coupon times a fixed rate in currency c1 and receives a coupon times a fixed rate in currency c2 times current FX rate divided by the FX rate at the inception of the deal. However, the cash flows are always guaranteed to be positive for the investor. The investor, therefore, has the option to receive cash flows making the payoff similar to a Bermudan style FX option. The swap house is, thus, selling a series of Currency options with a floating rate as a premium; the rate is usually subtracted with a spread.
where
Model
The pricing of PRDCs used to be done using 3-factor grid/lattice or Monte Carlo models where one factor represents the short rate in currency1; the second factor the short rate in currency2; and the third factor the movement in the FX rate between currency1 and currency2.
Model choice for the interest rate factors varies – for speed reasons, popular choices are Hull–White model, Black–Karasinski model, and extended Cheyette Model.
FX model choice also varies among houses – popular choices are Dupire-type local volatility models, stochastic SABR Volatility Models, or models which allow mixing of the two.
Nowadays, most dealers use a variant of the industry-standard LIBOR market model to price the PRDCs.
Inputs
- Correlation constants between each factor. Those correlation parameters are usually estimated historically or calibrated to market prices
- FX volatility calibrated to FX Options and user inputs
- IRS volatilities of each currency calibrated based on IRS Swaptions and yield curves
- Yield curve of money market rate1 and rate2 based on deposit rates, futures prices and swap rates
- Basis swap spread curves
- Spot FX rate
Computation
Plain vanilla PRDCs can be broken down into a string of vanilla options.
For Callable PRDCs – which are not replicable – the present value and the risks are now computed using quasi-Monte Carlo simulations and can take several hours. The same can be said of the TARN PRDCs and Chooser PRDCs (which are also callable).
Hedging
A plain vanilla PRDC is exposed to the movements in interest rates, FX, volatility (on both interest rates and fx), correlation and basis. Those risks are hedged with interest rate swaps in each currency to reduce interest rate risk, interest rate swaptions in each currency to reduce interest rate volatility exposures, FX Options to reduce FX volatility exposures and Basis swaps to reduce basis risk. Correlation exposure can be partially hedged with correlation swaps.
While such hedges are theoretically possible, there are a lot of practical difficulties, largely due to the following situation. The owners of the PRDC notes, usually retail investors, don't hedge their risks in the market. Only the banks, which are all short the notes, actively hedge and rebalance their positions. In other words, if there is a significant move in FX, for example, all the PRDC books will need the same kind of FX volatility rebalancing at the same time. The note holders would be the natural counterparty for the hedge, but they don't take part in this market (similar to buyers of portfolio insurance in 1987). This situation often creates "one way markets" and sometimes liquidity squeeze situations in long-term FX volatilities, basis swaps or long end AUD interest rate swaps.
The volume of PRDC notes issued has been so large that the hedging and rebalancing requirements far exceed the available liquidity in several key markets. However every model is derived under the assumption that there is sufficient liquidity – in other words, they are potentially mispricing the trades because in this market, a few of the key standard Black–Scholes assumptions (such as zero transaction cost, unlimited liquidity, no jumps in price) break down. No active secondary market ever existed for PRDC and banks usually mark their books to some consensus level provided by an independent company. Anecdotal evidence indicates that nobody would show a bid anywhere close to that consensus level.
PRDC during the Subprime Crisis
PRDC has been the subject of much attention in the market during the subprime mortgage crisis. By the nature of the trade, investment banks hedging the risks for PRDC structured note issuers will have a short cross-gamma position between FX volatility, interest rate and FX. In a volatile market where market parameters move in large and correlated steps, investment banks are forced to rebalance their hedges at a loss, often daily.
In particular, when FX spot goes up, the hedger for a PRDC note is expected to pay more coupons on a PRDC note. Thus, the hedger is more likely to call the note, reducing the expected duration of the note. In this situation, the hedger has to partially unwind the hedges done at the inception of the PRDC note. For example, the hedge would have to pay swaps in the foreign currency. If FX spot moves in a correlated fashion with the foreign currency swap rate (that is, foreign currency swap rate increases as FX spot increases), the hedger would need to pay a higher swap rate as FX spot goes up, and receive a lower swap rate as FX spot goes down. This is an example of how the hedger of a PRDC note is short cross gamma.
This was the main driver behind the increased market volatility in FX skew, long-dated FX volatility, long-dated Japanese Yen and Australian dollar interest rate, especially during the last quarter of 2008.
See also
References
- "Structured Notes Market" (PDF).