
In radio engineering and telecommunications, standing wave ratio (SWR) is a measure of impedance matching of loads to the characteristic impedance of a transmission line or waveguide. Impedance mismatches result in standing waves along the transmission line, and SWR is defined as the ratio of the partial standing wave's amplitude at an antinode (maximum) to the amplitude at a node (minimum) along the line.
Voltage standing wave ratio (VSWR) (pronounced "vizwar") is the ratio of maximum to minimum voltage on a transmission line . For example, a VSWR of 1.2 means a peak voltage 1.2 times the minimum voltage along that line, if the line is at least one half wavelength long.
A SWR can be also defined as the ratio of the maximum amplitude to minimum amplitude of the transmission line's currents, electric field strength, or the magnetic field strength. Neglecting transmission line loss, these ratios are identical.
The power standing wave ratio (PSWR) is defined as the square of the VSWR, however, this deprecated term has no direct physical relation to power actually involved in transmission.
SWR is usually measured using a dedicated instrument called an SWR meter. Since SWR is a measure of the load impedance relative to the characteristic impedance of the transmission line in use (which together determine the reflection coefficient as described below), a given SWR meter can interpret the impedance it sees in terms of SWR only if it has been designed for the same particular characteristic impedance as the line. In practice most transmission lines used in these applications are coaxial cables with an impedance of either 50 or 75 ohms, so most SWR meters correspond to one of these.
Checking the SWR is a standard procedure in a radio station. Although the same information could be obtained by measuring the load's impedance with an impedance analyzer (or "impedance bridge"), the SWR meter is simpler and more robust for this purpose. By measuring the magnitude of the impedance mismatch at the transmitter output it reveals problems due to either the antenna or the transmission line.
Impedance matching
Main article: Impedance matchingSWR is used as a measure of impedance matching of a load to the characteristic impedance of a transmission line carrying radio frequency (RF) signals. This especially applies to transmission lines connecting radio transmitters and receivers with their antennas, as well as similar uses of RF cables such as cable television connections to TV receivers and distribution amplifiers. Impedance matching is achieved when the source impedance is the complex conjugate of the load impedance. The easiest way of achieving this, and the way that minimizes losses along the transmission line, is for the imaginary part of the complex impedance of both the source and load to be zero, that is, pure resistances, equal to the characteristic impedance of the transmission line. When there is a mismatch between the load impedance and the transmission line, part of the forward wave sent toward the load is reflected back along the transmission line towards the source. The source then sees a different impedance than it expects which can lead to lesser (or in some cases, more) power being supplied by it, the result being very sensitive to the electrical length of the transmission line.
Such a mismatch is usually undesired and results in standing waves along the transmission line which magnifies transmission line losses (significant at higher frequencies and for longer cables). The SWR is a measure of the depth of those standing waves and is, therefore, a measure of the matching of the load to the transmission line. A matched load would result in an SWR of 1:1 implying no reflected wave. An infinite SWR represents complete reflection by a load unable to absorb electrical power, with all the incident power reflected back towards the source.
It should be understood that the match of a load to the transmission line is different from the match of a source to the transmission line or the match of a source to the load seen through the transmission line. For instance, if there is a perfect match between the load impedance Zload and the source impedance Zsource = Zload, that perfect match will remain if the source and load are connected through a transmission line with an electrical length of one half wavelength (or a multiple of one half wavelengths) using a transmission line of any characteristic impedance Z0. However the SWR will generally not be 1:1, depending only on Zload and Z0. With a different length of transmission line, the source will see a different impedance than Zload which may or may not be a good match to the source. Sometimes this is deliberate, as when a quarter-wave matching section is used to improve the match between an otherwise mismatched source and load.
However typical RF sources such as transmitters and signal generators are designed to look into a purely resistive load impedance such as 50Ω or 75Ω, corresponding to common transmission lines' characteristic impedances. In those cases, matching the load to the transmission line, Zload = Z0, always ensures that the source will see the same load impedance as if the transmission line weren't there. This is identical to a 1:1 SWR. This condition (Zload = Z0) also means that the load seen by the source is independent of the transmission line's electrical length. Since the electrical length of a physical segment of transmission line depends on the signal frequency, violation of this condition means that the impedance seen by the source through the transmission line becomes a function of frequency (especially if the line is long), even if Zload is frequency-independent. So in practice, a good SWR (near 1:1) implies a transmitter's output seeing the exact impedance it expects for optimum and safe operation.
Relationship to the reflection coefficient
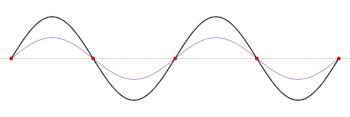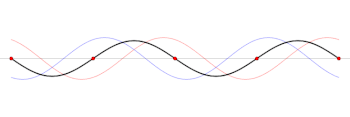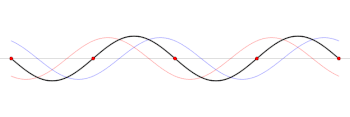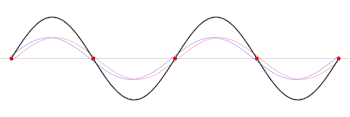

The voltage component of a standing wave in a uniform transmission line consists of the forward wave (with complex amplitude ) superimposed on the reflected wave (with complex amplitude ).
A wave is partly reflected when a transmission line is terminated with an impedance unequal to its characteristic impedance. The reflection coefficient can be defined as:
or
is a complex number that describes both the magnitude and the phase shift of the reflection. The simplest cases with measured at the load are:
- : complete negative reflection, when the line is short-circuited,
- : no reflection, when the line is perfectly matched,
- : complete positive reflection, when the line is open-circuited.
The SWR directly corresponds to the magnitude of .
At some points along the line the forward and reflected waves interfere constructively, exactly in phase, with the resulting amplitude given by the sum of those waves' amplitudes:
At other points, the waves interfere 180° out of phase with the amplitudes partially cancelling:
The voltage standing wave ratio is then
Since the magnitude of always falls in the range , the SWR is always greater than or equal to unity. Note that the phase of Vf and Vr vary along the transmission line in opposite directions to each other. Therefore, the complex-valued reflection coefficient varies as well, but only in phase. With the SWR dependent only on the complex magnitude of , it can be seen that the SWR measured at any point along the transmission line (neglecting transmission line losses) obtains an identical reading.
Since the power of the forward and reflected waves are proportional to the square of the voltage components due to each wave, SWR can be expressed in terms of forward and reflected power:
By sampling the complex voltage and current at the point of insertion, an SWR meter is able to compute the effective forward and reflected voltages on the transmission line for the characteristic impedance for which the SWR meter has been designed. Since the forward and reflected power is related to the square of the forward and reflected voltages, some SWR meters also display the forward and reflected power.
In the special case of a load RL, which is purely resistive but unequal to the characteristic impedance of the transmission line Z0, the SWR is given simply by their ratio:
with the ratio or its reciprocal is chosen to obtain a value greater than unity.
The standing wave pattern
Using complex notation for the voltage amplitudes, for a signal at frequency f, the actual (real) voltages Vactual as a function of time t are understood to relate to the complex voltages according to:
Thus taking the real part of the complex quantity inside the parenthesis, the actual voltage consists of a sine wave at frequency f with a peak amplitude equal to the complex magnitude of V, and with a phase given by the phase of the complex V. Then with the position along a transmission line given by x, with the line ending in a load located at xo, the complex amplitudes of the forward and reverse waves would be written as:
for some complex amplitude A (corresponding to the forward wave at xo that some treatments use phasors where the time dependence is according to and spatial dependence (for a wave in the +x direction) of Either convention obtains the same result for Vactual.
According to the superposition principle the net voltage present at any point x on the transmission line is equal to the sum of the voltages due to the forward and reflected waves:
Since we are interested in the variations of the magnitude of Vnet along the line (as a function of x), we shall solve instead for the squared magnitude of that quantity, which simplifies the mathematics. To obtain the squared magnitude we multiply the above quantity by its complex conjugate:
Depending on the phase of the third term, the maximum and minimum values of Vnet (the square root of the quantity in the equations) are and respectively, for a standing wave ratio of:
as earlier asserted. Along the line, the above expression for is seen to oscillate sinusoidally between and with a period of 2π /2k . This is half of the guided wavelength λ = 2π / k for the frequency f . That can be seen as due to interference between two waves of that frequency which are travelling in opposite directions.
For example, at a frequency f = 20 MHz (free space wavelength of 15 m) in a transmission line whose velocity factor is 0.67 , the guided wavelength (distance between voltage peaks of the forward wave alone) would be λ = 10 m . At instances when the forward wave at x = 0 is at zero phase (peak voltage) then at x = 10 m it would also be at zero phase, but at x = 5 m it would be at 180° phase (peak negative voltage). On the other hand, the magnitude of the voltage due to a standing wave produced by its addition to a reflected wave, would have a wavelength between peaks of only 1/2λ = 5 m . Depending on the location of the load and phase of reflection, there might be a peak in the magnitude of Vnet at x = 1.3 m . Then there would be another peak found where |Vnet| = Vmax at x = 6.3 m , whereas it would find minima of the standing wave at x = 3.8 m, 8.8 m, etc.
Practical implications of SWR

The most common case for measuring and examining SWR is when installing and tuning transmitting antennas. When a transmitter is connected to an antenna by a feed line, the driving point impedance of the antenna must match the characteristic impedance of the feed line in order for the transmitter to see the impedance it was designed for (the impedance of the feed line, usually 50 or 75 ohms).
The impedance of a particular antenna design can vary due to a number of factors that cannot always be clearly identified. This includes the transmitter frequency (as compared to the antenna's design or resonant frequency), the antenna's height above and quality of the ground, proximity to large metal structures, and variations in the exact size of the conductors used to construct the antenna.
When an antenna and feed line do not have matching impedances, the transmitter sees an unexpected impedance, where it might not be able to produce its full power, and can even damage the transmitter in some cases. The reflected power in the transmission line increases the average current and therefore losses in the transmission line compared to power actually delivered to the load. It is the interaction of these reflected waves with forward waves which causes standing wave patterns, with the negative repercussions we have noted.
Matching the impedance of the antenna to the impedance of the feed line can sometimes be accomplished through adjusting the antenna itself, but otherwise is possible using an antenna tuner, an impedance matching device. Installing the tuner between the feed line and the antenna allows for the feed line to see a load close to its characteristic impedance, while sending most of the transmitter's power (a small amount may be dissipated within the tuner) to be radiated by the antenna despite its otherwise unacceptable feed point impedance. Installing a tuner in between the transmitter and the feed line can also transform the impedance seen at the transmitter end of the feed line to one preferred by the transmitter. However, in the latter case, the feed line still has a high SWR present, with the resulting increased feed line losses unmitigated.
The magnitude of those losses are dependent on the type of transmission line, and its length. They always increase with frequency. For example, a certain antenna used well away from its resonant frequency may have an SWR of 6:1. For a frequency of 3.5 MHz, with that antenna fed through 75 meters of RG-8A coax, the loss due to standing waves would be 2.2 dB. However the same 6:1 mismatch through 75 meters of RG-8A coax would incur 10.8 dB of loss at 146 MHz. Thus, a better match of the antenna to the feed line, that is, a lower SWR, becomes increasingly important with increasing frequency, even if the transmitter is able to accommodate the impedance seen (or an antenna tuner is used between the transmitter and feed line).
Certain types of transmissions can suffer other negative effects from reflected waves on a transmission line. Analog TV can experience "ghosts" from delayed signals bouncing back and forth on a long line. FM stereo can also be affected and digital signals can experience delayed pulses leading to bit errors. Whenever the delay times for a signal going back down and then again up the line are comparable to the modulation time constants, effects occur. For this reason, these types of transmissions require a low SWR on the feedline, even if SWR induced loss might be acceptable and matching is done at the transmitter.
Methods of measuring standing wave ratio

Many different methods can be used to measure standing wave ratio. The most intuitive method uses a slotted line which is a section of transmission line with an open slot which allows a probe to detect the actual voltage at various points along the line.
Thus the maximum and minimum values can be compared directly. This method is used at VHF and higher frequencies. At lower frequencies, such lines are impractically long.
Directional couplers can be used at HF through microwave frequencies. Some are a quarter wave or more long, which restricts their use to the higher frequencies. Other types of directional couplers sample the current and voltage at a single point in the transmission path and mathematically combine them in such a way as to represent the power flowing in one direction. The common type of SWR / power meter used in amateur operation may contain a dual directional coupler. Other types use a single coupler which can be rotated 180 degrees to sample power flowing in either direction. Unidirectional couplers of this type are available for many frequency ranges and power levels and with appropriate coupling values for the analog meter used.

The forward and reflected power measured by directional couplers can be used to calculate SWR. The computations can be done mathematically in analog or digital form or by using graphical methods built into the meter as an additional scale or by reading from the crossing point between two needles on the same meter. The above measuring instruments can be used "in line" that is, the full power of the transmitter can pass through the measuring device so as to allow continuous monitoring of SWR. Other instruments, such as network analyzers, low power directional couplers and antenna bridges use low power for the measurement and must be connected in place of the transmitter. Bridge circuits can be used to directly measure the real and imaginary parts of a load impedance and to use those values to derive SWR. These methods can provide more information than just SWR or forward and reflected power. Stand alone antenna analyzers use various measuring methods and can display SWR and other parameters plotted against frequency. By using directional couplers and a bridge in combination, it is possible to make an in line instrument that reads directly in complex impedance or in SWR. Stand alone antenna analyzers also are available that measure multiple parameters.
Power standing wave ratio
The term power standing wave ratio (PSWR) is sometimes referred to, and defined as, the square of the voltage standing wave ratio. The term is widely cited as "misleading".
The expression "power standing-wave ratio", which may sometimes be encountered, is even more misleading, for the power distribution along a loss-free line is constant. ...
— J.H. Gridley (2014)
However it does correspond to one type of measurement of SWR using what was formerly a standard measuring instrument at microwave frequencies, the slotted line. The slotted line is a waveguide (or air-filled coaxial line) in which a small sensing antenna which is part of a crystal detector or detector is placed in the electric field in the line. The voltage induced in the antenna is rectified by either a point contact diode (crystal rectifier) or a Schottky barrier diode that is incorporated in the detector. These detectors have a square law output for low levels of input. Readings therefore corresponded to the square of the electric field along the slot, E(x), with maximum and minimum readings of Emax and Emin found as the probe is moved along the slot. The ratio of these yields the square of the SWR, the so-called PSWR.
This technique of rationalization of terms is fraught with problems. The square law behavior of the detector diode is exhibited only when the voltage across the diode is below the knee of the diode. Once the detected voltage exceeds the knee, the response of the diode becomes nearly linear. In this mode the diode and its associated filtering capacitor produce a voltage that is proportional to the peak of the sampled voltage. The operator of such a detector would not have a ready indication as to the mode in which the detector diode is operating and therefore differentiating the results between SWR or so called PSWR is not practical. Perhaps even worse, is the common case where the minimum detected voltage is below the knee and the maximum voltage is above the knee. In this case, the computed results are largely meaningless. Thus the terms PSWR and Power Standing Wave Ratio are deprecated and should be considered only from a legacy measurement perspective.
Implications of SWR on medical applications
SWR can also have a detrimental impact upon the performance of microwave-based medical applications. In microwave electrosurgery an antenna that is placed directly into tissue may not always have an optimal match with the feedline resulting in an SWR. The presence of SWR can affect monitoring components used to measure power levels impacting the reliability of such measurements.
See also
- Antenna tuner ("transmatch")
- Impedance
- Impedance matching
- Mismatch loss
- Return loss
- SWR meter
- Time-domain reflectometer
- Total active reflection coefficient
References
- Knott, Eugene F.; Shaeffer, John F.; Tuley, Michael T. (2004). Radar cross section. SciTech Radar and Defense Series (2nd ed.). SciTech Publishing. p. 374. ISBN 978-1-891121-25-8.
- Schaub, Keith B.; Kelly, Joe (2004). Production testing of RF and system-on-a-chip devices for wireless communications. Artech House microwave library. Artech House. p. 93. ISBN 978-1-58053-692-9.
- Silver, Samuel (1984) . Microwave Antenna Theory and Design. IEE. p. 28. ISBN 0863410170.
- Sliusar, I.; Slyusar, V.; Voloshko, S.; Zinchenko, A.; Utkin, Y. (22–27 June 2020). Synthesis of a broadband ring antenna of a two-tape design (PDF). 12th International Conference on Antenna Theory and Techniques (ICATT-2020). Kharkiv, Ukraine. Archived (PDF) from the original on 2022-10-09.
- ^ Hutchinson, Chuck, ed. (2000). The ARRL Handbook for Radio Amateurs 2001. Newington, CT: American Radio Relay League. pp. 19.4 – 19.6, 19.13, 20.2. ISBN 978-0-87259-186-8.
- Ford, Steve (April 1994), "The SWR obsession" (PDF), QST Magazine, vol. 78, no. 4, Newington, CT: American Radio Relay League, pp. 70–72, retrieved 2014-11-04
- Terman, Fredrick E. (1952). Electronic Measurements. McGraw Hill. p. 135 ff. LCCN 51-12650.
-
Schulz, Glenn B., (W9IQ) (January 24, 2018). "How does an SWR meter really work?". ham.stackexchange.com. Retrieved March 18, 2018.
{{cite web}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - "Nautel adds two models to NX series". Nautel (Press release). March 11, 2015. Archived from the original on August 18, 2016. Retrieved July 6, 2017.
- "Model OIB-1 and OIB-3". www.deltaelectronics.com. Delta Electronics, Inc.
- Wolff, Christian. "Standing wave ratio". radartutorial.eu.
- Gridley, J.H. (2014). Principles of Electrical Transmission Lines in Power and Communication. Elsevier. p. 265. ISBN 978-1483186030 – via Google Books.
- Rollin, Bernard Vincent (1964). An Introduction to Electronics. Clarendon Press. p. 209. OCLC 1148924.
- "Problems with VSWR in medical applications". microwaves101.com. Retrieved July 6, 2017.
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
Further reading
- Understanding the Fundamental Principles of Vector Network Analysis (PDF) (Report). Application note. Vol. 1287–1. Hewlett-Packard. 1997. Archived (PDF) from the original on 2022-10-09.
External links
- "Standing wave diagram". poynting.herokuapp.com. Archived from the original on 2020-11-25. Retrieved 2015-07-09. — A web application that draws the Standing Wave Diagram and calculates the SWR, input impedance, reflection coefficient and more
- "Reflection and VSWR". fourier-series.com. RF concepts. — A flash demonstration of transmission line reflection and SWR
- "VSWR". telestrian.co.uk. — An online conversion tool between SWR, return loss and reflection coefficient
- "Online VSWR Calculator". emtalk.com.
- "VSWR tutorial". electronics-notes.com. antennas & propagation. — Series of pages dealing with all aspects of VSWR, reflection coefficient, return loss, practical aspects, measurement, etc.
 ) superimposed on the reflected wave (with complex amplitude
) superimposed on the reflected wave (with complex amplitude  ).
).
 can be defined as:
can be defined as:


 : complete negative reflection, when the line is short-circuited,
: complete negative reflection, when the line is short-circuited, : no reflection, when the line is perfectly matched,
: no reflection, when the line is perfectly matched, : complete positive reflection, when the line is open-circuited.
: complete positive reflection, when the line is open-circuited. given by the sum of those waves' amplitudes:
given by the sum of those waves' amplitudes:







 and spatial dependence (for a wave in the +x direction) of
and spatial dependence (for a wave in the +x direction) of  Either convention obtains the same result for Vactual.
Either convention obtains the same result for Vactual.


 and
and  respectively, for a standing wave ratio of:
respectively, for a standing wave ratio of:


 is seen to oscillate sinusoidally between
is seen to oscillate sinusoidally between  and
and  with a period of 2π /2k . This is half of the guided wavelength λ = 2π / k for the frequency f . That can be seen as due to interference between two waves of that frequency which are travelling in opposite directions.
with a period of 2π /2k . This is half of the guided wavelength λ = 2π / k for the frequency f . That can be seen as due to interference between two waves of that frequency which are travelling in opposite directions.