In algebraic geometry, a proper morphism between schemes is an analog of a proper map between complex analytic spaces.
Some authors call a proper variety over a field a complete variety. For example, every projective variety over a field is proper over . A scheme of finite type over the complex numbers (for example, a variety) is proper over C if and only if the space (C) of complex points with the classical (Euclidean) topology is compact and Hausdorff.
A closed immersion is proper. A morphism is finite if and only if it is proper and quasi-finite.
Definition
A morphism of schemes is called universally closed if for every scheme with a morphism , the projection from the fiber product
is a closed map of the underlying topological spaces. A morphism of schemes is called proper if it is separated, of finite type, and universally closed ( II, 5.4.1 ). One also says that is proper over . In particular, a variety over a field is said to be proper over if the morphism is proper.
Examples
For any natural number n, projective space P over a commutative ring R is proper over R. Projective morphisms are proper, but not all proper morphisms are projective. For example, there is a smooth proper complex variety of dimension 3 which is not projective over C. Affine varieties of positive dimension over a field k are never proper over k. More generally, a proper affine morphism of schemes must be finite. For example, it is not hard to see that the affine line A over a field k is not proper over k, because the morphism A → Spec(k) is not universally closed. Indeed, the pulled-back morphism
(given by (x,y) ↦ y) is not closed, because the image of the closed subset xy = 1 in A × A = A is A − 0, which is not closed in A.
Properties and characterizations of proper morphisms
In the following, let f: X → Y be a morphism of schemes.
- The composition of two proper morphisms is proper.
- Any base change of a proper morphism f: X → Y is proper. That is, if g: Z → Y is any morphism of schemes, then the resulting morphism X ×Y Z → Z is proper.
- Properness is a local property on the base (in the Zariski topology). That is, if Y is covered by some open subschemes Yi and the restriction of f to all f(Yi) is proper, then so is f.
- More strongly, properness is local on the base in the fpqc topology. For example, if X is a scheme over a field k and E is a field extension of k, then X is proper over k if and only if the base change XE is proper over E.
- Closed immersions are proper.
- More generally, finite morphisms are proper. This is a consequence of the going up theorem.
- By Deligne, a morphism of schemes is finite if and only if it is proper and quasi-finite. This had been shown by Grothendieck if the morphism f: X → Y is locally of finite presentation, which follows from the other assumptions if Y is noetherian.
- For X proper over a scheme S, and Y separated over S, the image of any morphism X → Y over S is a closed subset of Y. This is analogous to the theorem in topology that the image of a continuous map from a compact space to a Hausdorff space is a closed subset.
- The Stein factorization theorem states that any proper morphism to a locally noetherian scheme can be factored as X → Z → Y, where X → Z is proper, surjective, and has geometrically connected fibers, and Z → Y is finite.
- Chow's lemma says that proper morphisms are closely related to projective morphisms. One version is: if X is proper over a quasi-compact scheme Y and X has only finitely many irreducible components (which is automatic for Y noetherian), then there is a projective surjective morphism g: W → X such that W is projective over Y. Moreover, one can arrange that g is an isomorphism over a dense open subset U of X, and that g(U) is dense in W. One can also arrange that W is integral if X is integral.
- Nagata's compactification theorem, as generalized by Deligne, says that a separated morphism of finite type between quasi-compact and quasi-separated schemes factors as an open immersion followed by a proper morphism.
- Proper morphisms between locally noetherian schemes preserve coherent sheaves, in the sense that the higher direct images Rf∗(F) (in particular the direct image f∗(F)) of a coherent sheaf F are coherent (EGA III, 3.2.1). (Analogously, for a proper map between complex analytic spaces, Grauert and Remmert showed that the higher direct images preserve coherent analytic sheaves.) As a very special case: the ring of regular functions on a proper scheme X over a field k has finite dimension as a k-vector space. By contrast, the ring of regular functions on the affine line over k is the polynomial ring k, which does not have finite dimension as a k-vector space.
- There is also a slightly stronger statement of this:(EGA III, 3.2.4) let be a morphism of finite type, S locally noetherian and a -module. If the support of F is proper over S, then for each the higher direct image is coherent.
- For a scheme X of finite type over the complex numbers, the set X(C) of complex points is a complex analytic space, using the classical (Euclidean) topology. For X and Y separated and of finite type over C, a morphism f: X → Y over C is proper if and only if the continuous map f: X(C) → Y(C) is proper in the sense that the inverse image of every compact set is compact.
- If f: X→Y and g: Y→Z are such that gf is proper and g is separated, then f is proper. This can for example be easily proven using the following criterion.
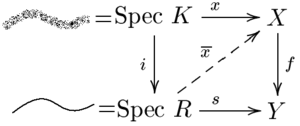
Valuative criterion of properness
There is a very intuitive criterion for properness which goes back to Chevalley. It is commonly called the valuative criterion of properness. Let f: X → Y be a morphism of finite type of Noetherian schemes. Then f is proper if and only if for all discrete valuation rings R with fraction field K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to . (EGA II, 7.3.8). More generally, a quasi-separated morphism f: X → Y of finite type (note: finite type includes quasi-compact) of 'any' schemes X, Y is proper if and only if for all valuation rings R with fraction field K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to . (Stacks project Tags 01KF and 01KY). Noting that Spec K is the generic point of Spec R and discrete valuation rings are precisely the regular local one-dimensional rings, one may rephrase the criterion: given a regular curve on Y (corresponding to the morphism s: Spec R → Y) and given a lift of the generic point of this curve to X, f is proper if and only if there is exactly one way to complete the curve.
Similarly, f is separated if and only if in every such diagram, there is at most one lift .
For example, given the valuative criterion, it becomes easy to check that projective space P is proper over a field (or even over Z). One simply observes that for a discrete valuation ring R with fraction field K, every K-point of projective space comes from an R-point, by scaling the coordinates so that all lie in R and at least one is a unit in R.
Geometric interpretation with disks
One of the motivating examples for the valuative criterion of properness is the interpretation of as an infinitesimal disk, or complex-analytically, as the disk . This comes from the fact that every power series
converges in some disk of radius around the origin. Then, using a change of coordinates, this can be expressed as a power series on the unit disk. Then, if we invert , this is the ring which are the power series which may have a pole at the origin. This is represented topologically as the open disk with the origin removed. For a morphism of schemes over , this is given by the commutative diagram
Then, the valuative criterion for properness would be a filling in of the point in the image of .
Example
It's instructive to look at a counter-example to see why the valuative criterion of properness should hold on spaces analogous to closed compact manifolds. If we take and , then a morphism factors through an affine chart of , reducing the diagram to
where is the chart centered around on . This gives the commutative diagram of commutative algebras
Then, a lifting of the diagram of schemes, , would imply there is a morphism sending from the commutative diagram of algebras. This, of course, cannot happen. Therefore is not proper over .
Geometric interpretation with curves
There is another similar example of the valuative criterion of properness which captures some of the intuition for why this theorem should hold. Consider a curve and the complement of a point . Then the valuative criterion for properness would read as a diagram
with a lifting of . Geometrically this means every curve in the scheme can be completed to a compact curve. This bit of intuition aligns with what the scheme-theoretic interpretation of a morphism of topological spaces with compact fibers, that a sequence in one of the fibers must converge. Because this geometric situation is a problem locally, the diagram is replaced by looking at the local ring , which is a DVR, and its fraction field . Then, the lifting problem then gives the commutative diagram
where the scheme represents a local disk around with the closed point removed.
Proper morphism of formal schemes
Let be a morphism between locally noetherian formal schemes. We say f is proper or is proper over if (i) f is an adic morphism (i.e., maps the ideal of definition to the ideal of definition) and (ii) the induced map is proper, where and K is the ideal of definition of .(EGA III, 3.4.1) The definition is independent of the choice of K.
For example, if g: Y → Z is a proper morphism of locally noetherian schemes, Z0 is a closed subset of Z, and Y0 is a closed subset of Y such that g(Y0) ⊂ Z0, then the morphism on formal completions is a proper morphism of formal schemes.
Grothendieck proved the coherence theorem in this setting. Namely, let be a proper morphism of locally noetherian formal schemes. If F is a coherent sheaf on , then the higher direct images are coherent.
See also
References
- Hartshorne (1977), Appendix B, Example 3.4.1.
- Liu (2002), Lemma 3.3.17.
- Stacks Project, Tag 02YJ.
- Grothendieck, EGA IV, Part 4, Corollaire 18.12.4; Stacks Project, Tag 02LQ.
- Grothendieck, EGA IV, Part 3, Théorème 8.11.1.
- Stacks Project, Tag 01W0.
- Stacks Project, Tag 03GX.
- Grothendieck, EGA II, Corollaire 5.6.2.
- Conrad (2007), Theorem 4.1.
- SGA 1, XII Proposition 3.2.
- Grothendieck, EGA III, Part 1, Théorème 3.4.2.
- SGA1 Revêtements étales et groupe fondamental, 1960–1961 (Étale coverings and the fundamental group), Lecture Notes in Mathematics 224, 1971
- Conrad, Brian (2007), "Deligne's notes on Nagata compactifications" (PDF), Journal of the Ramanujan Mathematical Society, 22: 205–257, MR 2356346
- Grothendieck, Alexandre; Dieudonné, Jean (1961). "Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques classes de morphismes". Publications Mathématiques de l'IHÉS. 8: 5–222. doi:10.1007/bf02699291. MR 0217084., section 5.3. (definition of properness), section 7.3. (valuative criterion of properness)
- Grothendieck, Alexandre; Dieudonné, Jean (1961). "Eléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Première partie". Publications Mathématiques de l'IHÉS. 11: 5–167. doi:10.1007/bf02684274. MR 0217085.
- Grothendieck, Alexandre; Dieudonné, Jean (1966). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Troisième partie". Publications Mathématiques de l'IHÉS. 28: 5–255. doi:10.1007/bf02684343. MR 0217086., section 15.7. (generalizations of valuative criteria to not necessarily noetherian schemes)
- Grothendieck, Alexandre; Dieudonné, Jean (1967). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième partie". Publications Mathématiques de l'IHÉS. 32: 5–361. doi:10.1007/bf02732123. MR 0238860.
- Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
- Liu, Qing (2002), Algebraic geometry and arithmetic curves, Oxford: Oxford University Press, ISBN 9780191547805, MR 1917232
External links
- V.I. Danilov (2001) , "Proper morphism", Encyclopedia of Mathematics, EMS Press
- The Stacks Project Authors, The Stacks Project
 a
a  of
of  of schemes is called universally closed if for every scheme
of schemes is called universally closed if for every scheme  with a morphism
with a morphism  , the projection from the
, the projection from the 
 . In particular, a variety
. In particular, a variety  is proper.
is proper.

 be a morphism of finite type, S locally noetherian and
be a morphism of finite type, S locally noetherian and  a
a  -module. If the support of F is proper over S, then for each
-module. If the support of F is proper over S, then for each  the
the  is coherent.
is coherent. . (EGA II, 7.3.8). More generally, a quasi-separated morphism f: X → Y of finite type (note: finite type includes quasi-compact) of 'any' schemes X, Y is proper if and only if for all
. (EGA II, 7.3.8). More generally, a quasi-separated morphism f: X → Y of finite type (note: finite type includes quasi-compact) of 'any' schemes X, Y is proper if and only if for all ![{\displaystyle {\text{Spec}}(\mathbb {C} ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc33c099b18393b811b4bc4b36b47da7e99dfdf7) as an infinitesimal disk, or complex-analytically, as the disk
as an infinitesimal disk, or complex-analytically, as the disk  . This comes from the fact that every power series
. This comes from the fact that every power series
 around the origin. Then, using a change of coordinates, this can be expressed as a power series on the unit disk. Then, if we invert
around the origin. Then, using a change of coordinates, this can be expressed as a power series on the unit disk. Then, if we invert  , this is the ring
, this is the ring ![{\displaystyle \mathbb {C} ]=\mathbb {C} ((t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c613740aad26856289780a3dc2ae2c48ff8d57f3) which are the power series which may have a pole at the origin. This is represented topologically as the open disk
which are the power series which may have a pole at the origin. This is represented topologically as the open disk  with the origin removed. For a morphism of schemes over
with the origin removed. For a morphism of schemes over  , this is given by the commutative diagram
, this is given by the commutative diagram
 in the image of
in the image of  .
.
 and
and  , then a morphism
, then a morphism  factors through an affine chart of
factors through an affine chart of ![{\displaystyle {\begin{matrix}{\text{Spec}}(\mathbb {C} ((t)))&\to &{\text{Spec}}(\mathbb {C} )\\\downarrow &&\downarrow \\{\text{Spec}}(\mathbb {C} ])&\to &{\text{Spec}}(\mathbb {C} )\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c90137402723316fe7a1968b3e824759155f5242)
 is the chart centered around
is the chart centered around  on
on ![{\displaystyle {\begin{matrix}\mathbb {C} ((t))&\leftarrow &\mathbb {C} \\\uparrow &&\uparrow \\\mathbb {C} ]&\leftarrow &\mathbb {C} \end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f76b0e37164b97cc222831de9f43381d60bd05e3)
![{\displaystyle {\text{Spec}}(\mathbb {C} ])\to {\text{Spec}}(\mathbb {C} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddbfa815e4443f9d485c98ebcbd9666192b259e6) , would imply there is a morphism
, would imply there is a morphism ![{\displaystyle \mathbb {C} \to \mathbb {C} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf19229e3d790d3f24abb9b84f0cf192c83d3199) sending
sending  from the commutative diagram of algebras. This, of course, cannot happen. Therefore
from the commutative diagram of algebras. This, of course, cannot happen. Therefore  and the complement of a point
and the complement of a point  . Then the valuative criterion for properness would read as a diagram
. Then the valuative criterion for properness would read as a diagram
 . Geometrically this means every curve in the scheme
. Geometrically this means every curve in the scheme  , which is a DVR, and its fraction field
, which is a DVR, and its fraction field  . Then, the lifting problem then gives the commutative diagram
. Then, the lifting problem then gives the commutative diagram
 represents a local disk around
represents a local disk around  with the closed point
with the closed point  be a morphism between
be a morphism between  is proper over
is proper over  if (i) f is an
if (i) f is an  is proper, where
is proper, where  and K is the ideal of definition of
and K is the ideal of definition of  on formal completions is a proper morphism of formal schemes.
on formal completions is a proper morphism of formal schemes.