
Proportion is a central principle of architectural theory and an important connection between mathematics and art. It is the visual effect of the relationship of the various objects and spaces that make up a structure to one another and to the whole. These relationships are often governed by multiples of a standard unit of length known as a "module".
Proportion in architecture was discussed by Vitruvius, Leon Battista Alberti, Andrea Palladio, and Le Corbusier among others.
Roman architecture
Vitruvius
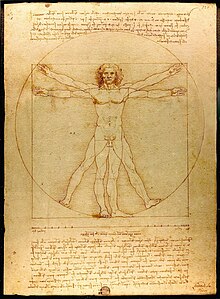


Architecture in Roman antiquity was rarely documented except in the writings of Vitruvius' treatise De architectura. Vitruvius served as an engineer under Julius Caesar during the first Gallic Wars (58–50 BC). The treatise was dedicated to Emperor Augustus. As Vitruvius defined the concept in the first chapters of the treatise, he mentioned the three prerequisites of architecture are firmness (firmitas), commodity (utilitas), and delight (venustas), which require the architects to be equipped with a varied kind of learning and knowledge of many branches. Moreover, Vitruvius identified the "Six Principles of Design" as order (ordinatio), arrangement (dispositio), proportion (eurythmia), symmetry (symmetria), propriety (decor) and economy (distributio). Among the six principles, proportion interrelates and supports all the other factors in geometrical forms and arithmetical ratios.
The word symmetria, usually translated to "symmetry" in modern renderings, in ancient times meant something more closely related to "mathematical harmony" and measurable proportions. Vitruvius tried to describe his theory in the makeup of the human body, which he referred to as the perfect or golden ratio. The principles of measurement units digit, foot, and cubit also came from the dimensions of a Vitruvian Man. More specifically, Vitruvius used the total height of 6 feet of a person, and each part of the body takes up a different ratio. For example, the face is about 1/10 of the total height, and the head is about 1/8 of the total height. Vitruvius used these ratios to prove that the composition of classical orders mimicked the human body, thereby ensuring aesthetic harmonization when people viewed architectural columns.
Classical architecture
In classical architecture, the module was established as the radius of the lower shaft of a classical column, with proportions expressed as a fraction or multiple of that module.
Le Corbusier
In his Le Modulor (1948), Le Corbusier presented a system of proportions which took the golden ratio and a man with a raised arm as the scalable modules of proportion.
See also
References
- James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 606-607.
- ^ Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. pp. 33–46. ISBN 978-0-300-08138-1.
- ^ Jones, Mark Wilson (2000). Principles of Roman Architecture. New Haven and London: Yale University Press. p. 41. ISBN 978-0-300-08138-1.
- James Stevens Curl (ed.), Oxford Dictionary of Architecture, 2nd ed. (Oxford, 2006), 496.
Further reading
- P. H. Scholfield (1958). The Theory of Proportion in Architecture. Cambridge University Press.
- Hanno-Walter Kruft (1994). History of Architectural Theory. Princeton Architectural Press. ISBN 9781568980102.
