| This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources. Find sources: "Proportional navigation" – news · newspapers · books · scholar · JSTOR (May 2024) |
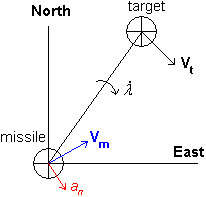

Proportional navigation (also known as PN or Pro-Nav) is a guidance law (analogous to proportional control) used in some form or another by most homing air target missiles. It is based on the fact that two vehicles are on a collision course when their direct line-of-sight does not change direction as the range closes. PN dictates that the missile velocity vector should rotate at a rate proportional to the rotation rate of the line of sight (Line-Of-Sight rate or LOS-rate), and in the same direction.
Where is the acceleration perpendicular to the missile's instantaneous velocity vector, is the proportionality constant generally having an integer value 3-5 (dimensionless), is the line of sight rate, and V is the closing velocity.
Since the line of sight is not in general co-linear with the missile velocity vector, the applied acceleration does not necessarily preserve the missile kinetic energy. In practice, in the absence of engine throttling capability, this type of control may not be possible.
Proportional navigation can also be achieved using an acceleration normal to the instantaneous velocity difference:
where is the rotation vector of the line of sight:
and is the target velocity relative to the missile and is the range from missile to target. This acceleration depends explicitly on the velocity difference vector, which may be difficult to obtain in practice. By contrast, in the expressions that follow, dependence is only on the change of the line of sight and the magnitude of the closing velocity. If acceleration normal to the instantaneous line of sight is desired (as in the initial description), then the following expression is valid:
If energy conserving control is required (as is the case when only using control surfaces), the following acceleration, which is orthogonal to the missile velocity, may be used:
A rather simple hardware implementation of this guidance law can be found in early AIM-9 Sidewinder missiles. These missiles use a rapidly rotating parabolic mirror as a seeker. Simple electronics detect the directional error the seeker has with its target (an IR source), and apply a moment to this gimballed mirror to keep it pointed at the target. Since the mirror is in fact a gyroscope it will keep pointing at the same direction if no external force or moment is applied, regardless of the movements of the missile. The voltage applied to the mirror while keeping it locked on the target is then also used (although amplified) to deflect the control surfaces that steer the missile, thereby making missile velocity vector rotation proportional to line of sight rotation. Although this does not result in a rotation rate that is always exactly proportional to the LOS-rate (which would require a constant airspeed), this implementation is equally effective.
The basis of proportional navigation was first discovered at sea, and was used by navigators on ships to avoid collisions. Commonly referred to as Constant Bearing Decreasing Range (CBDR), the concept continues to prove very useful for conning officers (the person in control of navigating the vessel at any point in time) because CBDR will result in a collision or near miss if action is not taken by one of the two vessels involved. Simply altering course until a change in bearing (obtained by compass sighting) occurs, will provide some assurance of avoidance of collision, obviously not foolproof: the conning officer of the vessel having made the course change must continually monitor bearing lest the other vessel does the same. Significant course change, rather than a modest alteration, is prudent. International Regulations for Preventing Collisions at Sea dictate which vessel must give way but they, of course, provide no guarantee that action will be taken by that vessel.
See also
Bibliography
- Yanushevsky, Rafael. Modern Missile Guidance. CRC Press, 2007. ISBN 978-1420062267.
References
- Yanushevsky, page 3.

 is the acceleration perpendicular to the missile's instantaneous velocity vector,
is the acceleration perpendicular to the missile's instantaneous velocity vector,  is the proportionality constant generally having an integer value 3-5 (dimensionless),
is the proportionality constant generally having an integer value 3-5 (dimensionless),  is the line of sight rate, and V is the closing velocity.
is the line of sight rate, and V is the closing velocity.

 is the
is the 
 is the target velocity relative to the missile and
is the target velocity relative to the missile and  is the range from missile to target. This acceleration depends explicitly on the velocity difference vector, which may be difficult to obtain in practice. By contrast, in the expressions that follow, dependence is only on the change of the line of sight and the magnitude of the closing velocity. If acceleration normal to the instantaneous line of sight is desired (as in the initial description), then the following expression is valid:
is the range from missile to target. This acceleration depends explicitly on the velocity difference vector, which may be difficult to obtain in practice. By contrast, in the expressions that follow, dependence is only on the change of the line of sight and the magnitude of the closing velocity. If acceleration normal to the instantaneous line of sight is desired (as in the initial description), then the following expression is valid:

