
In rheology, shear thinning is the non-Newtonian behavior of fluids whose viscosity decreases under shear strain. It is sometimes considered synonymous for pseudo-plastic behaviour, and is usually defined as excluding time-dependent effects, such as thixotropy.
Shear thinning is the most common type of non-Newtonian behavior of fluids and is seen in many industrial and everyday applications. Although shear thinning is generally not observed in pure liquids with low molecular mass or ideal solutions of small molecules like sucrose or sodium chloride, it is often observed in polymer solutions and molten polymers, as well as complex fluids and suspensions like ketchup, whipped cream, blood, paint, and nail polish.
Theories behind shear-thinning behaviour
Though the exact cause of shear thinning is not fully understood, it is widely regarded to be the effect of small structural changes within the fluid, such that microscale geometries within the fluid rearrange to facilitate shearing. In colloid systems, phase separation during flow leads to shear thinning. In polymer systems such as polymer melts and solutions, shear thinning is caused by the disentanglement of polymer chains during flow. At rest, high molecular weight polymers are entangled and randomly oriented. However, when undergoing agitation at a high enough rate, these highly anisotropic polymer chains start to disentangle and align along the direction of the shear force. This leads to less molecular/particle interaction and a larger amount of free space, decreasing the viscosity.
Power law model
Main article: Power-law fluid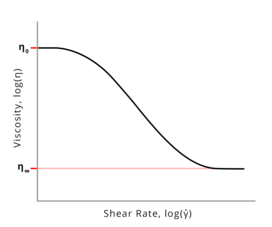
At both sufficiently high and very low shear rates, viscosity of a polymer system is independent of the shear rate. At high shear rates, polymers are entirely disentangled and the viscosity value of the system plateaus at η∞, or the infinite shear viscosity plateau. At low shear rates, the shear is too low to be impeded by entanglements and the viscosity value of the system is η0, or the zero shear rate viscosity. The value of η∞ represents the lowest viscosity attainable and may be orders of magnitude lower than η0, depending on the degree of shear thinning.
Viscosity is plotted against shear rate in a log(η) vs. log() plot, where the linear region is the shear-thinning regime and can be expressed using the Ostwald and de Waele power law equation:
The Ostwald and de Waele equation can be written in a logarithmic form:
The apparent viscosity is defined as , and this may be plugged into the Ostwald equation to yield a second power-law equation for apparent viscosity:
This expression can also be used to describe dilatant (shear thickening) behaviour, where the value of n is greater than 1.
Herschel–Bulkley model
See also: Herschel–Bulkley fluidBingham plastics require a critical shear stress to be exceeded in order to start flowing. This behaviour is usually seen in polymer/silica micro- and nanocomposites, where the formation of a silica network in the material provides a solid-like response at low shear stress. The shear-thinning behavior of plastic fluids can be described with the Herschel-Bulkley model, which adds a threshold shear stress component to the Ostwald equation:
Relationship with thixotropy
Some authors consider shear thinning to be a special case of thixotropic behaviour, because the recovery of the microstructure of the liquid to its initial state will always require a non-zero time. When the recovery of viscosity after disturbance is very rapid however, the observed behaviour is classic shear thinning or pseudoplasticity, because as soon as the shear is removed, the viscosity returns to normal. When it takes a measurable time for the viscosity to recover, thixotropic behaviour is observed. When describing the viscosity of liquids, however, it is therefore useful to distinguish shear-thinning (pseudoplastic) behaviour from thixotropic behaviour, where the viscosity at all shear rates is decreased for some duration after agitation: both of these effects can often be seen separately in the same liquid.
Everyday examples
Wall paint is a pseudoplastic material. When modern wall paint is applied, the shear created by the brush or roller will allow it to thin and wet out the surface evenly. Once applied, the paint regains its higher viscosity, which avoids drips and runs.
Ketchup is a shear-thinning material, viscous when at rest, but flowing at speed when agitated by squeezing, shaking, or striking the bottle.
Whipped cream is also a shear-thinning material. When whipped cream is sprayed out of its canister, it flows out smoothly from the nozzle due to the low viscosity at high flow rate. However, after whipped cream is sprayed into a spoon, it does not flow and its increased viscosity allows it to be rigid.
See also
- Non-Newtonian fluid – Fluid whose viscosity varies with the amount of force/stress applied to it
- Power-law fluid – Type of generalized Newtonian fluid
- Bingham plastic – Material which is solid at low stress but becomes viscous at high stress
- Rheology – Study of the flow of matter, primarily in a fluid state
- Kaye effect – Property of complex liquids
- Time-dependent viscosity
- Rheopecty: The longer the fluid is subjected to a shear strain, the higher the viscosity. Time-dependent shear thickening behavior.
- Thixotropy: The longer a fluid is subjected to a shear strain, the lower its viscosity. It is a time-dependent shear thinning behavior.
- Shear thickening: Similar to rheopecty, but independent of the passage of time.
- Thickening agent
- Paint thinner
External links
References
- Mezger, Thomas G. (2006). The rheology handbook : for users of rotational and oscillatory rheometers (2., rev. ed.). Hannover: Vincentz Network. p. 34. ISBN 9783878701743.
- Heldman, R. Paul Singh, Dennis R. (2013). Introduction to food engineering (5th ed.). Amsterdam: Elsevier. p. 160. ISBN 9780124016750.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Bair, Scott (2007). High-pressure rheology for quantitative elastohydrodynamics (1st ed.). Amsterdam: Elsevier. p. 136. ISBN 9780080475301. Retrieved 24 May 2015.
- ^ Malvern Instruments Worldwide. "A Basic Introduction to Rheology" (PDF). Retrieved 12 December 2019.
- Tazraei, P.; Riasi, A.; Takabi, B. (2015). "The influence of the non-Newtonian properties of blood on blood-hammer through the posterior cerebral artery". Mathematical Biosciences. 264: 119–127. doi:10.1016/j.mbs.2015.03.013. PMID 25865933.
- ^ "The Physics of Whipped Cream". NASA Science. 25 April 2008. Retrieved 20 August 2023.
- "Viscosity of Newtonian and Non-Newtonian Fluids". Rheosense Inc. Retrieved 12 December 2019.
- ^ "Flow Properties of Polymers". polymerdatabase.com. Retrieved 12 December 2019.
- Barnes, Howard A. (1997). "Thixotropy a review" (PDF). J. Non-Newtonian Fluid Mech., 70: 3. Archived from the original (PDF) on 30 April 2016. Retrieved 11 November 2011.
- Troy, David B. (2005). Remington : The science and practice of pharmacy (21st ed.). Philadelphia: Lippincott, Williams & Wilkins. p. 344. ISBN 9780781746731. Retrieved 24 May 2015.
- ^ Schlichting, H. Joachim (12 March 2021). "Ketchup Is Not Just a Condiment: It Is Also a Non-Newtonian Fluid". Scientific American. Retrieved 20 August 2023.
 ) plot, where the linear region is the shear-thinning regime and can be expressed using the Ostwald and de Waele power law equation:
) plot, where the linear region is the shear-thinning regime and can be expressed using the Ostwald and de Waele power law equation:


 , and this may be plugged into the Ostwald equation to yield a second power-law equation for apparent viscosity:
, and this may be plugged into the Ostwald equation to yield a second power-law equation for apparent viscosity:

