Misplaced Pages

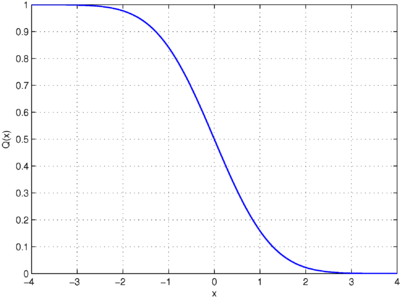
In statistics, the Q-function is the tail distribution function of the standard normal distribution. In other words, ${\displaystyle Q(x)}$ is the probability that a normal (Gaussian) random variable will obtain a value larger than ${\displaystyle x}$ standard deviations. Equivalently, ${\displaystyle Q(x)}$ is the probability that a standard normal random variable takes a value larger than ${\displaystyle x}$.

If ${\displaystyle Y}$ is a Gaussian random variable with mean ${\displaystyle \mu }$ and variance ${\displaystyle \sigma ^{2}}$, then ${\displaystyle X={\frac {Y-\mu }{\sigma }}}$ is standard normal and

${\displaystyle P(Y>y)=P(X>x)=Q(x)}$

where ${\displaystyle x={\frac {y-\mu }{\sigma }}}$.

Other definitions of the Q-function, all of which are simple transformations of the normal cumulative distribution function, are also used occasionally.

Because of its relation to the cumulative distribution function of the normal distribution, the Q-function can also be expressed in terms of the error function, which is an important function in applied mathematics and physics.

Definition and basic properties

Formally, the Q-function is defined as

${\displaystyle Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }\exp \left(-{\frac {u^{2}}{2}}\right)\,du.}$

Thus,

${\displaystyle Q(x)=1-Q(-x)=1-\Phi (x)\,\!,}$

where ${\displaystyle \Phi (x)}$ is the cumulative distribution function of the standard normal Gaussian distribution.

The Q-function can be expressed in terms of the error function, or the complementary error function, as

${\displaystyle {\begin{aligned}Q(x)&={\frac {1}{2}}\left({\frac {2}{\sqrt {\pi }}}\int _{x/{\sqrt {2}}}^{\infty }\exp \left(-t^{2}\right)\,dt\right)\\&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)~~{\text{ -or-}}\\&={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).\end{aligned}}}$

An alternative form of the Q-function known as Craig's formula, after its discoverer, is expressed as:

${\displaystyle Q(x)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}\right)d\theta .}$

This expression is valid only for positive values of x, but it can be used in conjunction with Q(x) = 1 − Q(−x) to obtain Q(x) for negative values. This form is advantageous in that the range of integration is fixed and finite.

Craig's formula was later extended by Behnad (2020) for the Q-function of the sum of two non-negative variables, as follows:

${\displaystyle Q(x+y)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}-{\frac {y^{2}}{2\cos ^{2}\theta }}\right)d\theta ,\quad x,y\geqslant 0.}$

Bounds and approximations

• The Q-function is not an elementary function. However, it can be upper and lower bounded as,

${\displaystyle \left({\frac {x}{1+x^{2}}}\right)\phi (x)<Q(x)<{\frac {\phi (x)}{x}},\qquad x>0,}$

where ${\displaystyle \phi (x)}$ is the density function of the standard normal distribution, and the bounds become increasingly tight for large x.

Using the substitution v =u/2, the upper bound is derived as follows:

${\displaystyle Q(x)=\int _{x}^{\infty }\phi (u)\,du<\int _{x}^{\infty }{\frac {u}{x}}\phi (u)\,du=\int _{\frac {x^{2}}{2}}^{\infty }{\frac {e^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl .}{\frac {e^{-v}}{x{\sqrt {2\pi }}}}{\biggr |}_{\frac {x^{2}}{2}}^{\infty }={\frac {\phi (x)}{x}}.}$

Similarly, using ${\displaystyle \phi '(u)=-u\phi (u)}$ and the quotient rule,

${\displaystyle \left(1+{\frac {1}{x^{2}}}\right)Q(x)=\int _{x}^{\infty }\left(1+{\frac {1}{x^{2}}}\right)\phi (u)\,du>\int _{x}^{\infty }\left(1+{\frac {1}{u^{2}}}\right)\phi (u)\,du=-{\biggl .}{\frac {\phi (u)}{u}}{\biggr |}_{x}^{\infty }={\frac {\phi (x)}{x}}.}$

Solving for Q(x) provides the lower bound.

The geometric mean of the upper and lower bound gives a suitable approximation for ${\displaystyle Q(x)}$:

${\displaystyle Q(x)\approx {\frac {\phi (x)}{\sqrt {1+x^{2}}}},\qquad x\geq 0.}$

• Tighter bounds and approximations of ${\displaystyle Q(x)}$ can also be obtained by optimizing the following expression

${\displaystyle {\tilde {Q}}(x)={\frac {\phi (x)}{(1-a)x+a{\sqrt {x^{2}+b}}}}.}$

For ${\displaystyle x\geq 0}$, the best upper bound is given by ${\displaystyle a=0.344}$ and ${\displaystyle b=5.334}$ with maximum absolute relative error of 0.44%. Likewise, the best approximation is given by ${\displaystyle a=0.339}$ and ${\displaystyle b=5.510}$ with maximum absolute relative error of 0.27%. Finally, the best lower bound is given by ${\displaystyle a=1/\pi }$ and ${\displaystyle b=2\pi }$ with maximum absolute relative error of 1.17%.

• The Chernoff bound of the Q-function is

${\displaystyle Q(x)\leq e^{-{\frac {x^{2}}{2}}},\qquad x>0}$

• Improved exponential bounds and a pure exponential approximation are

${\displaystyle Q(x)\leq {\tfrac {1}{4}}e^{-x^{2}}+{\tfrac {1}{4}}e^{-{\frac {x^{2}}{2}}}\leq {\tfrac {1}{2}}e^{-{\frac {x^{2}}{2}}},\qquad x>0}$

${\displaystyle Q(x)\approx {\frac {1}{12}}e^{-{\frac {x^{2}}{2}}}+{\frac {1}{4}}e^{-{\frac {2}{3}}x^{2}},\qquad x>0}$

• The above were generalized by Tanash & Riihonen (2020), who showed that ${\displaystyle Q(x)}$ can be accurately approximated or bounded by

${\displaystyle {\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.}$

In particular, they presented a systematic methodology to solve the numerical coefficients ${\displaystyle \{(a_{n},b_{n})\}_{n=1}^{N}}$ that yield a minimax approximation or bound: ${\displaystyle Q(x)\approx {\tilde {Q}}(x)}$, ${\displaystyle Q(x)\leq {\tilde {Q}}(x)}$, or ${\displaystyle Q(x)\geq {\tilde {Q}}(x)}$ for ${\displaystyle x\geq 0}$. With the example coefficients tabulated in the paper for ${\displaystyle N=20}$, the relative and absolute approximation errors are less than ${\displaystyle 2.831\cdot 10^{-6}}$ and ${\displaystyle 1.416\cdot 10^{-6}}$, respectively. The coefficients ${\displaystyle \{(a_{n},b_{n})\}_{n=1}^{N}}$ for many variations of the exponential approximations and bounds up to ${\displaystyle N=25}$ have been released to open access as a comprehensive dataset.

• Another approximation of ${\displaystyle Q(x)}$ for ${\displaystyle x\in [0,\infty )}$ is given by Karagiannidis & Lioumpas (2007) who showed for the appropriate choice of parameters ${\displaystyle \{A,B\}}$ that

${\displaystyle f(x;A,B)={\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi }}x}}\approx \operatorname {erfc} \left(x\right).}$

The absolute error between ${\displaystyle f(x;A,B)}$ and ${\displaystyle \operatorname {erfc} (x)}$ over the range ${\displaystyle }$ is minimized by evaluating

${\displaystyle \{A,B\}={\underset {\{A,B\}}{\arg \min }}{\frac {1}{R}}\int _{0}^{R}|f(x;A,B)-\operatorname {erfc} (x)|dx.}$

Using ${\displaystyle R=20}$ and numerically integrating, they found the minimum error occurred when ${\displaystyle \{A,B\}=\{1.98,1.135\},}$ which gave a good approximation for ${\displaystyle \forall x\geq 0.}$

Substituting these values and using the relationship between ${\displaystyle Q(x)}$ and ${\displaystyle \operatorname {erfc} (x)}$ from above gives

${\displaystyle Q(x)\approx {\frac {\left(1-e^{\frac {-1.98x}{\sqrt {2}}}\right)e^{-{\frac {x^{2}}{2}}}}{1.135{\sqrt {2\pi }}x}},x\geq 0.}$

Alternative coefficients are also available for the above 'Karagiannidis–Lioumpas approximation' for tailoring accuracy for a specific application or transforming it into a tight bound.

• A tighter and more tractable approximation of ${\displaystyle Q(x)}$ for positive arguments ${\displaystyle x\in [0,\infty )}$ is given by López-Benítez & Casadevall (2011) based on a second-order exponential function:

${\displaystyle Q(x)\approx e^{-ax^{2}-bx-c},\qquad x\geq 0.}$

The fitting coefficients ${\displaystyle (a,b,c)}$ can be optimized over any desired range of arguments in order to minimize the sum of square errors (${\displaystyle a=0.3842}$, ${\displaystyle b=0.7640}$, ${\displaystyle c=0.6964}$ for ${\displaystyle x\in }$) or minimize the maximum absolute error (${\displaystyle a=0.4920}$, ${\displaystyle b=0.2887}$, ${\displaystyle c=1.1893}$ for ${\displaystyle x\in }$). This approximation offers some benefits such as a good trade-off between accuracy and analytical tractability (for example, the extension to any arbitrary power of ${\displaystyle Q(x)}$ is trivial and does not alter the algebraic form of the approximation).

Inverse Q

The inverse Q-function can be related to the inverse error functions:

${\displaystyle Q^{-1}(y)={\sqrt {2}}\ \mathrm {erf} ^{-1}(1-2y)={\sqrt {2}}\ \mathrm {erfc} ^{-1}(2y)}$

The function ${\displaystyle Q^{-1}(y)}$ finds application in digital communications. It is usually expressed in dB and generally called Q-factor:

${\displaystyle \mathrm {Q{\text{-}}factor} =20\log _{10}\!\left(Q^{-1}(y)\right)\!~\mathrm {dB} }$

where y is the bit-error rate (BER) of the digitally modulated signal under analysis. For instance, for quadrature phase-shift keying (QPSK) in additive white Gaussian noise, the Q-factor defined above coincides with the value in dB of the signal to noise ratio that yields a bit error rate equal to y.

Values

The Q-function is well tabulated and can be computed directly in most of the mathematical software packages such as R and those available in Python, MATLAB and Mathematica. Some values of the Q-function are given below for reference.

Generalization to high dimensions

The Q-function can be generalized to higher dimensions:

${\displaystyle Q(\mathbf {x} )=\mathbb {P} (\mathbf {X} \geq \mathbf {x} ),}$

where ${\displaystyle \mathbf {X} \sim {\mathcal {N}}(\mathbf {0} ,\,\Sigma )}$ follows the multivariate normal distribution with covariance ${\displaystyle \Sigma }$ and the threshold is of the form ${\displaystyle \mathbf {x} =\gamma \Sigma \mathbf {l} ^{*}}$ for some positive vector ${\displaystyle \mathbf {l} ^{*}>\mathbf {0} }$ and positive constant ${\displaystyle \gamma >0}$. As in the one dimensional case, there is no simple analytical formula for the Q-function. Nevertheless, the Q-function can be approximated arbitrarily well as ${\displaystyle \gamma }$ becomes larger and larger.

References

1. "The Q-function". cnx.org. Archived from the original on 2012-02-29.
2. ^ "Basic properties of the Q-function" (PDF). 2009-03-05. Archived from the original (PDF) on 2009-03-25.
3. Normal Distribution Function – from Wolfram MathWorld
4. Craig, J.W. (1991). "A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations" (PDF). MILCOM 91 - Conference record. pp. 571–575. doi:10.1109/MILCOM.1991.258319. ISBN 0-87942-691-8. S2CID 16034807.
5. Behnad, Aydin (2020). "A Novel Extension to Craig's Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis". IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
6. Gordon, R.D. (1941). "Values of Mills' ratio of area to bounding ordinate and of the normal probability integral for large values of the argument". Ann. Math. Stat. 12 (3): 364–366. doi:10.1214/aoms/1177731721.
7. ^ Borjesson, P.; Sundberg, C.-E. (1979). "Simple Approximations of the Error Function Q(x) for Communications Applications". IEEE Transactions on Communications. 27 (3): 639–643. doi:10.1109/TCOM.1979.1094433.
8. Chiani, M.; Dardari, D.; Simon, M.K. (2003). "New exponential bounds and approximations for the computation of error probability in fading channels" (PDF). IEEE Transactions on Wireless Communications. 24 (5): 840–845. doi:10.1109/TWC.2003.814350.
9. Tanash, I.M.; Riihonen, T. (2020). "Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials". IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
10. Tanash, I.M.; Riihonen, T. (2020). "Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]". Zenodo. doi:10.5281/zenodo.4112978.
11. Karagiannidis, George; Lioumpas, Athanasios (2007). "An Improved Approximation for the Gaussian Q-Function" (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
12. Tanash, I.M.; Riihonen, T. (2021). "Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function". IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
13. Lopez-Benitez, Miguel; Casadevall, Fernando (2011). "Versatile, Accurate, and Analytically Tractable Approximation for the Gaussian Q-Function" (PDF). IEEE Transactions on Communications. 59 (4): 917–922. doi:10.1109/TCOMM.2011.012711.100105. S2CID 1145101.
14. Savage, I. R. (1962). "Mills ratio for multivariate normal distributions". Journal of Research of the National Bureau of Standards Section B. 66 (3): 93–96. doi:10.6028/jres.066B.011. Zbl 0105.12601.
15. Botev, Z. I. (2016). "The normal law under linear restrictions: simulation and estimation via minimax tilting". Journal of the Royal Statistical Society, Series B. 79: 125–148. arXiv:1603.04166. Bibcode:2016arXiv160304166B. doi:10.1111/rssb.12162. S2CID 88515228.
16. Botev, Z. I.; Mackinlay, D.; Chen, Y.-L. (2017). "Logarithmically efficient estimation of the tail of the multivariate normal distribution". 2017 Winter Simulation Conference (WSC). IEEE. pp. 1903–191. doi:10.1109/WSC.2017.8247926. ISBN 978-1-5386-3428-8. S2CID 4626481.

• Normal distribution
• Special functions
• Functions related to probability distributions