Rose curve with angular frequency 2
Rotated quadrifolium Quadrifolium created with gears Four-leaf clover . For the symmetrical shape framework, see Quatrefoil .
The quadrifolium (also known as four-leaved clover ) is a type of rose curve with an angular frequency of 2. It has the polar equation :
r
=
a
cos
(
2
θ
)
,
{\displaystyle r=a\cos(2\theta ),\,}
with corresponding algebraic equation
(
x
2
+
y
2
)
3
=
a
2
(
x
2
−
y
2
)
2
.
{\displaystyle (x^{2}+y^{2})^{3}=a^{2}(x^{2}-y^{2})^{2}.\,}
Rotated counter-clockwise by 45°, this becomes
r
=
a
sin
(
2
θ
)
{\displaystyle r=a\sin(2\theta )\,}
with corresponding algebraic equation
(
x
2
+
y
2
)
3
=
4
a
2
x
2
y
2
.
{\displaystyle (x^{2}+y^{2})^{3}=4a^{2}x^{2}y^{2}.\,}
In either form, it is a plane algebraic curve of genus zero.
The dual curve to the quadrifolium is
(
x
2
−
y
2
)
4
+
837
(
x
2
+
y
2
)
2
+
108
x
2
y
2
=
16
(
x
2
+
7
y
2
)
(
y
2
+
7
x
2
)
(
x
2
+
y
2
)
+
729
(
x
2
+
y
2
)
.
{\displaystyle (x^{2}-y^{2})^{4}+837(x^{2}+y^{2})^{2}+108x^{2}y^{2}=16(x^{2}+7y^{2})(y^{2}+7x^{2})(x^{2}+y^{2})+729(x^{2}+y^{2}).\,}
Dual quadrifolium The area inside the quadrifolium is
1
2
π
a
2
{\displaystyle {\tfrac {1}{2}}\pi a^{2}}
perimeter of the quadrifolium is
8
a
E
(
3
2
)
=
4
π
a
(
(
52
3
−
90
)
M
′
(
1
,
7
−
4
3
)
M
2
(
1
,
7
−
4
3
)
+
7
−
4
3
M
(
1
,
7
−
4
3
)
)
{\displaystyle 8a\operatorname {E} \left({\frac {\sqrt {3}}{2}}\right)=4\pi a\left({\frac {(52{\sqrt {3}}-90)\operatorname {M} '(1,7-4{\sqrt {3}})}{\operatorname {M} ^{2}(1,7-4{\sqrt {3}})}}+{\frac {7-4{\sqrt {3}}}{\operatorname {M} (1,7-4{\sqrt {3}})}}\right)}
where
E
(
k
)
{\displaystyle \operatorname {E} (k)}
complete elliptic integral of the second kind with modulus
k
{\displaystyle k}
M
{\displaystyle \operatorname {M} }
arithmetic–geometric mean and
′
{\displaystyle '}
derivative with respect to the second variable.
Notes
Elementary Geometry of Algebraic Curves, An Undergraduate Introduction , Cambridge University Press, Cambridge, 2001, ISBN 978-0-521-64641-3 . Pages 92 and 93
Quadrifolium - from Wolfram MathWorld
References
External links
Category :
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.
**DISCLAIMER** We are not affiliated with Wikipedia, and Cloudflare.
The information presented on this site is for general informational purposes only and does not constitute medical advice.
You should always have a personal consultation with a healthcare professional before making changes to your diet, medication, or exercise routine.
AI helps with the correspondence in our chat.
We participate in an affiliate program. If you buy something through a link, we may earn a commission 💕
↑


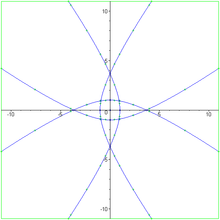





 , which is exactly half of the area of the circumcircle of the quadrifolium. The
, which is exactly half of the area of the circumcircle of the quadrifolium. The 
 is the
is the  ,
,  is the
is the  denotes the
denotes the