Misplaced Pages

Ranklet

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Statistical method for pattern recognition.
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.
Find sources: "Ranklet" – news · newspapers · books · scholar · JSTOR (June 2022)
This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (June 2022) (Learn how and when to remove this message)
(Learn how and when to remove this message)

In statistics, a ranklet is an orientation-selective non-parametric feature which is based on the computation of Mann–Whitney–Wilcoxon (MWW) rank-sum test statistics. Ranklets achieve similar response to Haar wavelets as they share the same pattern of orientation-selectivity, multi-scale nature and a suitable notion of completeness. There were invented by Fabrizio Smeralhi in 2002.

Rank-based (non-parametric) features have become popular in the field of image processing for their robustness in detecting outliers and invariance to monotonic transformations such as brightness, contrast changes and gamma correction.

The MWW is a combination of Wilcoxon rank-sum test and Mann–Whitney U-test. It is a non-parametric alternative to the t-test used to test the hypothesis for the comparison of two independent distributions. It assesses whether two samples of observations, usually referred as Treatment T and Control C, come from the same distribution but do not have to be normally distributed.

The Wilcoxon rank-sum statistics Ws is determined as:

W s = ∑ i = 1 N π i V i  where  π i = rank of element  i  and  V i = { 0  for  π i ∈ C 1  for  π i ∈ T {\displaystyle W_{s}=\sum _{i=1}^{N}\pi _{i}V_{i}{\text{ where }}\pi _{i}={\text{rank of element }}i{\text{ and }}V_{i}={\begin{cases}0&{\text{ for }}\pi _{i}\in C\\1&{\text{ for }}\pi _{i}\in T\end{cases}}}

Subsequently, let MW be the Mann–Whitney statistics defined by:

M W = W s − m ( m + 1 ) 2 {\displaystyle MW=W_{s}-{\frac {m(m+1)}{2}}}

where m is the number of Treatment values.

A ranklet R is defined as the normalization of MW in the range :

R = M W m n / 2 − 1 {\displaystyle R={\frac {MW}{mn/2}}-1}

where a positive value means that the Treatment region is brighter than the Control region, and a negative value otherwise.

Example

Suppose T = { 5 , 9 , 1 , 10 , 15 } {\displaystyle T=\lbrace 5,9,1,10,15\rbrace } and C = { 20 , 4 , 7 , 13 , 19 , 11 } {\displaystyle C=\lbrace 20,4,7,13,19,11\rbrace } then

Intensity 1 4 5 7 9 10 11 13 15 19 20
Sample T C T C T T C C T C C
Rank 1 2 3 4 5 6 7 8 9 10 11
  • W s = { 1 + 3 + 5 + 6 + 9 } = 24 {\displaystyle W_{s}={\Big \lbrace }1+3+5+6+9{\Big \rbrace }=24}
  • M W = 24 − [ 5 × ( 5 + 1 ) / 2 ] = 9 {\displaystyle MW=24-=9}
  • R = [ 9 / [ 5 × 6 / 2 ] ] − 1 = − 0.4 {\displaystyle R=]-1=-0.4}

Hence, in the above example the Control region was a little bit brighter than the Treatment region.

Method

Since Ranklets are non-linear filters, they can only be applied in the spatial domain. Filtering with Ranklets involves dividing an image window W into Treatment and Control regions as shown in the image below:

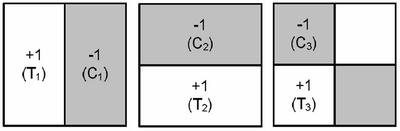
Orientation-Selective Ranklets
Orientation-Selective Ranklets

Subsequently, Wilcoxon rank-sum test statistics are computed in order to determine the intensity variations among conveniently chosen regions (according to the required orientation) of the samples in W. The intensity values of both regions are then replaced by the respective ranking scores. These ranking scores determine a pairwise comparison between the T and C regions. This means that a ranklet essentially counts the number of TxC pairs which are brighter in the T set. Hence a positive value means that the Treatment values are brighter than the Control values, and vice versa.

References

  1. "www.Ranklets.net". www.eecs.qmul.ac.uk. Retrieved 2022-06-05.
  2. Smeraldi, F. (August 2002). "Ranklets: Orientation selective non-parametric features applied to face detection". Object recognition supported by user interaction for service robots. Vol. 3. pp. 379–382. doi:10.1109/ICPR.2002.1047924. ISBN 0-7695-1695-X. S2CID 16667804. {{cite book}}: Check |isbn= value: checksum (help)
  3. "www.Ranklets.net". www.eecs.qmul.ac.uk. Retrieved 2022-06-05.

External links

Categories: