Rendering method

In 3D computer graphics, ray tracing is a technique for modeling light transport for use in a wide variety of rendering algorithms for generating digital images.
On a spectrum of computational cost and visual fidelity, ray tracing-based rendering techniques, such as ray casting, recursive ray tracing, distribution ray tracing, photon mapping and path tracing, are generally slower and higher fidelity than scanline rendering methods. Thus, ray tracing was first deployed in applications where taking a relatively long time to render could be tolerated, such as still CGI images, and film and television visual effects (VFX), but was less suited to real-time applications such as video games, where speed is critical in rendering each frame.
Since 2019, however, hardware acceleration for real-time ray tracing has become standard on new commercial graphics cards, and graphics APIs have followed suit, allowing developers to use hybrid ray tracing and rasterization-based rendering in games and other real-time applications with a lesser hit to frame render times.
Ray tracing is capable of simulating a variety of optical effects, such as reflection, refraction, soft shadows, scattering, depth of field, motion blur, caustics, ambient occlusion and dispersion phenomena (such as chromatic aberration). It can also be used to trace the path of sound waves in a similar fashion to light waves, making it a viable option for more immersive sound design in video games by rendering realistic reverberation and echoes. In fact, any physical wave or particle phenomenon with approximately linear motion can be simulated with ray tracing.
Ray tracing-based rendering techniques that involve sampling light over a domain generate image noise artifacts that can be addressed by tracing a very large number of rays or using denoising techniques.
History


The idea of ray tracing comes from as early as the 16th century when it was described by Albrecht Dürer, who is credited for its invention. Dürer described multiple techniques for projecting 3-D scenes onto an image plane. Some of these project chosen geometry onto the image plane, as is done with rasterization today. Others determine what geometry is visible along a given ray, as is done with ray tracing.
Using a computer for ray tracing to generate shaded pictures was first accomplished by Arthur Appel in 1968. Appel used ray tracing for primary visibility (determining the closest surface to the camera at each image point) by tracing a ray through each point to be shaded into the scene to identify the visible surface. The closest surface intersected by the ray was the visible one. This non-recursive ray tracing-based rendering algorithm is today called "ray casting". His algorithm then traced secondary rays to the light source from each point being shaded to determine whether the point was in shadow or not.
Later, in 1971, Goldstein and Nagel of MAGI (Mathematical Applications Group, Inc.) published "3-D Visual Simulation", wherein ray tracing was used to make shaded pictures of solids. At the ray-surface intersection point found, they computed the surface normal and, knowing the position of the light source, computed the brightness of the pixel on the screen. Their publication describes a short (30 second) film “made using the University of Maryland’s display hardware outfitted with a 16mm camera. The film showed the helicopter and a simple ground level gun emplacement. The helicopter was programmed to undergo a series of maneuvers including turns, take-offs, and landings, etc., until it eventually is shot down and crashed.” A CDC 6600 computer was used. MAGI produced an animation video called MAGI/SynthaVision Sampler in 1974.
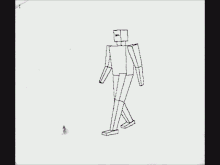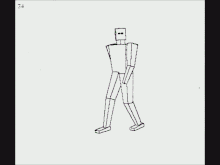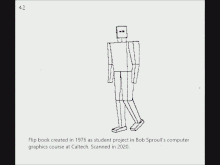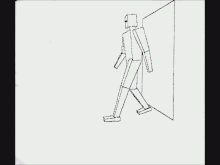
Another early instance of ray casting came in 1976, when Scott Roth created a flip book animation in Bob Sproull's computer graphics course at Caltech. The scanned pages are shown as a video on the right. Roth's computer program noted an edge point at a pixel location if the ray intersected a bounded plane different from that of its neighbors. Of course, a ray could intersect multiple planes in space, but only the surface point closest to the camera was noted as visible. The platform was a DEC PDP-10, a Tektronix storage-tube display, and a printer which would create an image of the display on rolling thermal paper. Roth extended the framework, introduced the term ray casting in the context of computer graphics and solid modeling, and in 1982 published his work while at GM Research Labs.
Turner Whitted was the first to show recursive ray tracing for mirror reflection and for refraction through translucent objects, with an angle determined by the solid's index of refraction, and to use ray tracing for anti-aliasing. Whitted also showed ray traced shadows. He produced a recursive ray-traced film called The Compleat Angler in 1979 while an engineer at Bell Labs. Whitted's deeply recursive ray tracing algorithm reframed rendering from being primarily a matter of surface visibility determination to being a matter of light transport. His paper inspired a series of subsequent work by others that included distribution ray tracing and finally unbiased path tracing, which provides the rendering equation framework that has allowed computer generated imagery to be faithful to reality.
For decades, global illumination in major films using computer-generated imagery was approximated with additional lights. Ray tracing-based rendering eventually changed that by enabling physically-based light transport. Early feature films rendered entirely using path tracing include Monster House (2006), Cloudy with a Chance of Meatballs (2009), and Monsters University (2013).
Algorithm overview


Optical ray tracing describes a method for producing visual images constructed in 3-D computer graphics environments, with more photorealism than either ray casting or scanline rendering techniques. It works by tracing a path from an imaginary eye through each pixel in a virtual screen, and calculating the color of the object visible through it.
Scenes in ray tracing are described mathematically by a programmer or by a visual artist (normally using intermediary tools). Scenes may also incorporate data from images and models captured by means such as digital photography.
Typically, each ray must be tested for intersection with some subset of all the objects in the scene. Once the nearest object has been identified, the algorithm will estimate the incoming light at the point of intersection, examine the material properties of the object, and combine this information to calculate the final color of the pixel. Certain illumination algorithms and reflective or translucent materials may require more rays to be re-cast into the scene.
It may at first seem counterintuitive or "backward" to send rays away from the camera, rather than into it (as actual light does in reality), but doing so is many orders of magnitude more efficient. Since the overwhelming majority of light rays from a given light source do not make it directly into the viewer's eye, a "forward" simulation could potentially waste a tremendous amount of computation on light paths that are never recorded.
Therefore, the shortcut taken in ray tracing is to presuppose that a given ray intersects the view frame. After either a maximum number of reflections or a ray traveling a certain distance without intersection, the ray ceases to travel and the pixel's value is updated.
Calculate rays for rectangular viewport
On input we have (in calculation we use vector normalization and cross product):
- eye position
- target position
- field of view - for humans, we can assume
- numbers of square pixels on viewport vertical and horizontal direction
- numbers of actual pixel
- vertical vector which indicates where is up and down, usually - roll component which determine viewport rotation around point C (where the axis of rotation is the ET section)
The idea is to find the position of each viewport pixel center which allows us to find the line going from eye through that pixel and finally get the ray described by point and vector (or its normalisation ). First we need to find the coordinates of the bottom left viewport pixel and find the next pixel by making a shift along directions parallel to viewport (vectors i ) multiplied by the size of the pixel. Below we introduce formulas which include distance between the eye and the viewport. However, this value will be reduced during ray normalization (so you might as well accept that and remove it from calculations).
Pre-calculations: let's find and normalise vector and vectors which are parallel to the viewport (all depicted on above picture)
note that viewport center , next we calculate viewport sizes divided by 2 including inverse aspect ratio
and then we calculate next-pixel shifting vectors along directions parallel to viewport (), and left bottom pixel center
Calculations: note and ray so
Detailed description of ray tracing computer algorithm and its genesis
What happens in nature (simplified)
See also: Electromagnetism and Quantum electrodynamicsIn nature, a light source emits a ray of light which travels, eventually, to a surface that interrupts its progress. One can think of this "ray" as a stream of photons traveling along the same path. In a perfect vacuum this ray will be a straight line (ignoring relativistic effects). Any combination of four things might happen with this light ray: absorption, reflection, refraction and fluorescence. A surface may absorb part of the light ray, resulting in a loss of intensity of the reflected and/or refracted light. It might also reflect all or part of the light ray, in one or more directions. If the surface has any transparent or translucent properties, it refracts a portion of the light beam into itself in a different direction while absorbing some (or all) of the spectrum (and possibly altering the color). Less commonly, a surface may absorb some portion of the light and fluorescently re-emit the light at a longer wavelength color in a random direction, though this is rare enough that it can be discounted from most rendering applications. Between absorption, reflection, refraction and fluorescence, all of the incoming light must be accounted for, and no more. A surface cannot, for instance, reflect 66% of an incoming light ray, and refract 50%, since the two would add up to be 116%. From here, the reflected and/or refracted rays may strike other surfaces, where their absorptive, refractive, reflective and fluorescent properties again affect the progress of the incoming rays. Some of these rays travel in such a way that they hit our eye, causing us to see the scene and so contribute to the final rendered image.
Ray casting algorithm
Main article: Ray castingThe idea behind ray casting, the predecessor to recursive ray tracing, is to trace rays from the eye, one per pixel, and find the closest object blocking the path of that ray. Think of an image as a screen-door, with each square in the screen being a pixel. This is then the object the eye sees through that pixel. Using the material properties and the effect of the lights in the scene, this algorithm can determine the shading of this object. The simplifying assumption is made that if a surface faces a light, the light will reach that surface and not be blocked or in shadow. The shading of the surface is computed using traditional 3-D computer graphics shading models. One important advantage ray casting offered over older scanline algorithms was its ability to easily deal with non-planar surfaces and solids, such as cones and spheres. If a mathematical surface can be intersected by a ray, it can be rendered using ray casting. Elaborate objects can be created by using solid modeling techniques and easily rendered.
Volume ray casting algorithm
Main article: Volume ray castingIn the method of volume ray casting, each ray is traced so that color and/or density can be sampled along the ray and then be combined into a final pixel color. This is often used when objects cannot be easily represented by explicit surfaces (such as triangles), for example when rendering clouds or 3D medical scans.
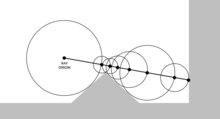
SDF ray marching algorithm
Main article: Ray marching § Distance-aided ray marchingIn SDF ray marching, or sphere tracing, each ray is traced in multiple steps to approximate an intersection point between the ray and a surface defined by a signed distance function (SDF). The SDF is evaluated for each iteration in order to be able take as large steps as possible without missing any part of the surface. A threshold is used to cancel further iteration when a point is reached that is close enough to the surface. This method is often used for 3-D fractal rendering.
Recursive ray tracing algorithm




Earlier algorithms traced rays from the eye into the scene until they hit an object, but determined the ray color without recursively tracing more rays. Recursive ray tracing continues the process. When a ray hits a surface, additional rays may be cast because of reflection, refraction, and shadow.:
- A reflection ray is traced in the mirror-reflection direction. The closest object it intersects is what will be seen in the reflection.
- A refraction ray traveling through transparent material works similarly, with the addition that a refractive ray could be entering or exiting a material. Turner Whitted extended the mathematical logic for rays passing through a transparent solid to include the effects of refraction.
- A shadow ray is traced toward each light. If any opaque object is found between the surface and the light, the surface is in shadow and the light does not illuminate it.
These recursive rays add more realism to ray traced images.
Advantages over other rendering methods
Ray tracing-based rendering's popularity stems from its basis in a realistic simulation of light transport, as compared to other rendering methods, such as rasterization, which focuses more on the realistic simulation of geometry. Effects such as reflections and shadows, which are difficult to simulate using other algorithms, are a natural result of the ray tracing algorithm. The computational independence of each ray makes ray tracing amenable to a basic level of parallelization, but the divergence of ray paths makes high utilization under parallelism quite difficult to achieve in practice.
Disadvantages
A serious disadvantage of ray tracing is performance (though it can in theory be faster than traditional scanline rendering depending on scene complexity vs. number of pixels on-screen). Until the late 2010s, ray tracing in real time was usually considered impossible on consumer hardware for nontrivial tasks. Scanline algorithms and other algorithms use data coherence to share computations between pixels, while ray tracing normally starts the process anew, treating each eye ray separately. However, this separation offers other advantages, such as the ability to shoot more rays as needed to perform spatial anti-aliasing and improve image quality where needed.
Whitted-style recursive ray tracing handles interreflection and optical effects such as refraction, but is not generally photorealistic. Improved realism occurs when the rendering equation is fully evaluated, as the equation conceptually includes every physical effect of light flow. However, this is infeasible given the computing resources required, and the limitations on geometric and material modeling fidelity. Path tracing is an algorithm for evaluating the rendering equation and thus gives a higher fidelity simulations of real-world lighting.
Reversed direction of traversal of scene by the rays
The process of shooting rays from the eye to the light source to render an image is sometimes called backwards ray tracing, since it is the opposite direction photons actually travel. However, there is confusion with this terminology. Early ray tracing was always done from the eye, and early researchers such as James Arvo used the term backwards ray tracing to mean shooting rays from the lights and gathering the results. Therefore, it is clearer to distinguish eye-based versus light-based ray tracing.
While the direct illumination is generally best sampled using eye-based ray tracing, certain indirect effects can benefit from rays generated from the lights. Caustics are bright patterns caused by the focusing of light off a wide reflective region onto a narrow area of (near-)diffuse surface. An algorithm that casts rays directly from lights onto reflective objects, tracing their paths to the eye, will better sample this phenomenon. This integration of eye-based and light-based rays is often expressed as bidirectional path tracing, in which paths are traced from both the eye and lights, and the paths subsequently joined by a connecting ray after some length.
Photon mapping is another method that uses both light-based and eye-based ray tracing; in an initial pass, energetic photons are traced along rays from the light source so as to compute an estimate of radiant flux as a function of 3-dimensional space (the eponymous photon map itself). In a subsequent pass, rays are traced from the eye into the scene to determine the visible surfaces, and the photon map is used to estimate the illumination at the visible surface points. The advantage of photon mapping versus bidirectional path tracing is the ability to achieve significant reuse of photons, reducing computation, at the cost of statistical bias.
An additional problem occurs when light must pass through a very narrow aperture to illuminate the scene (consider a darkened room, with a door slightly ajar leading to a brightly lit room), or a scene in which most points do not have direct line-of-sight to any light source (such as with ceiling-directed light fixtures or torchieres). In such cases, only a very small subset of paths will transport energy; Metropolis light transport is a method which begins with a random search of the path space, and when energetic paths are found, reuses this information by exploring the nearby space of rays.

To the right is an image showing a simple example of a path of rays recursively generated from the camera (or eye) to the light source using the above algorithm. A diffuse surface reflects light in all directions.
First, a ray is created at an eyepoint and traced through a pixel and into the scene, where it hits a diffuse surface. From that surface the algorithm recursively generates a reflection ray, which is traced through the scene, where it hits another diffuse surface. Finally, another reflection ray is generated and traced through the scene, where it hits the light source and is absorbed. The color of the pixel now depends on the colors of the first and second diffuse surface and the color of the light emitted from the light source. For example, if the light source emitted white light and the two diffuse surfaces were blue, then the resulting color of the pixel is blue.
Example
As a demonstration of the principles involved in ray tracing, consider how one would find the intersection between a ray and a sphere. This is merely the math behind the line–sphere intersection and the subsequent determination of the colour of the pixel being calculated. There is, of course, far more to the general process of ray tracing, but this demonstrates an example of the algorithms used.
In vector notation, the equation of a sphere with center and radius is
Any point on a ray starting from point with direction (here is a unit vector) can be written as
where is its distance between and . In our problem, we know , , (e.g. the position of a light source) and , and we need to find . Therefore, we substitute for :
Let for simplicity; then
Knowing that d is a unit vector allows us this minor simplification:
This quadratic equation has solutions
The two values of found by solving this equation are the two ones such that are the points where the ray intersects the sphere.
Any value which is negative does not lie on the ray, but rather in the opposite half-line (i.e. the one starting from with opposite direction).
If the quantity under the square root (the discriminant) is negative, then the ray does not intersect the sphere.
Let us suppose now that there is at least a positive solution, and let be the minimal one. In addition, let us suppose that the sphere is the nearest object on our scene intersecting our ray, and that it is made of a reflective material. We need to find in which direction the light ray is reflected. The laws of reflection state that the angle of reflection is equal and opposite to the angle of incidence between the incident ray and the normal to the sphere.
The normal to the sphere is simply
where is the intersection point found before. The reflection direction can be found by a reflection of with respect to , that is
Thus the reflected ray has equation
Now we only need to compute the intersection of the latter ray with our field of view, to get the pixel which our reflected light ray will hit. Lastly, this pixel is set to an appropriate color, taking into account how the color of the original light source and the one of the sphere are combined by the reflection.
Adaptive depth control
Adaptive depth control means that the renderer stops generating reflected/transmitted rays when the computed intensity becomes less than a certain threshold. There must always be a set maximum depth or else the program would generate an infinite number of rays. But it is not always necessary to go to the maximum depth if the surfaces are not highly reflective. To test for this the ray tracer must compute and keep the product of the global and reflection coefficients as the rays are traced.
Example: let Kr = 0.5 for a set of surfaces. Then from the first surface the maximum contribution is 0.5, for the reflection from the second: 0.5 × 0.5 = 0.25, the third: 0.25 × 0.5 = 0.125, the fourth: 0.125 × 0.5 = 0.0625, the fifth: 0.0625 × 0.5 = 0.03125, etc. In addition we might implement a distance attenuation factor such as 1/D2, which would also decrease the intensity contribution.
For a transmitted ray we could do something similar but in that case the distance traveled through the object would cause even faster intensity decrease. As an example of this, Hall & Greenberg found that even for a very reflective scene, using this with a maximum depth of 15 resulted in an average ray tree depth of 1.7.
Bounding volumes
Enclosing groups of objects in sets of bounding volume hierarchies (BVH) decreases the amount of computations required for ray tracing. A cast ray is first tested for an intersection with the bounding volume, and then if there is an intersection, the volume is recursively divided until the ray hits the object. The best type of bounding volume will be determined by the shape of the underlying object or objects. For example, if the objects are long and thin, then a sphere will enclose mainly empty space compared to a box. Boxes are also easier to generate hierarchical bounding volumes.
Note that using a hierarchical system like this (assuming it is done carefully) changes the intersection computational time from a linear dependence on the number of objects to something between linear and a logarithmic dependence. This is because, for a perfect case, each intersection test would divide the possibilities by two, and result in a binary tree type structure. Spatial subdivision methods, discussed below, try to achieve this. Furthermore, this acceleration structure makes the ray-tracing computation output-sensitive. I.e. the complexity of the ray intersection calculations depends on the number of objects that actually intersect the rays and not (only) on the number of objects in the scene.
Kay & Kajiya give a list of desired properties for hierarchical bounding volumes:
- Subtrees should contain objects that are near each other and the further down the tree the closer should be the objects.
- The volume of each node should be minimal.
- The sum of the volumes of all bounding volumes should be minimal.
- Greater attention should be placed on the nodes near the root since pruning a branch near the root will remove more potential objects than one farther down the tree.
- The time spent constructing the hierarchy should be much less than the time saved by using it.
Interactive ray tracing
See also: Ray-tracing hardwareThe first implementation of an interactive ray tracer was the LINKS-1 Computer Graphics System built in 1982 at Osaka University's School of Engineering, by professors Ohmura Kouichi, Shirakawa Isao and Kawata Toru with 50 students. It was a massively parallel processing computer system with 514 microprocessors (257 Zilog Z8001s and 257 iAPX 86s), used for 3-D computer graphics with high-speed ray tracing. According to the Information Processing Society of Japan: "The core of 3-D image rendering is calculating the luminance of each pixel making up a rendered surface from the given viewpoint, light source, and object position. The LINKS-1 system was developed to realize an image rendering methodology in which each pixel could be parallel processed independently using ray tracing. By developing a new software methodology specifically for high-speed image rendering, LINKS-1 was able to rapidly render highly realistic images." It was used to create an early 3-D planetarium-like video of the heavens made completely with computer graphics. The video was presented at the Fujitsu pavilion at the 1985 International Exposition in Tsukuba." It was the second system to do so after the Evans & Sutherland Digistar in 1982. The LINKS-1 was claimed by the designers to be the world's most powerful computer in 1984.
The next interactive ray tracer, and the first known to have been labeled "real-time" was credited at the 2005 SIGGRAPH computer graphics conference as being the REMRT/RT tools developed in 1986 by Mike Muuss for the BRL-CAD solid modeling system. Initially published in 1987 at USENIX, the BRL-CAD ray tracer was an early implementation of a parallel network distributed ray tracing system that achieved several frames per second in rendering performance. This performance was attained by means of the highly optimized yet platform independent LIBRT ray tracing engine in BRL-CAD and by using solid implicit CSG geometry on several shared memory parallel machines over a commodity network. BRL-CAD's ray tracer, including the REMRT/RT tools, continue to be available and developed today as open source software.
Since then, there have been considerable efforts and research towards implementing ray tracing at real-time speeds for a variety of purposes on stand-alone desktop configurations. These purposes include interactive 3-D graphics applications such as demoscene productions, computer and video games, and image rendering. Some real-time software 3-D engines based on ray tracing have been developed by hobbyist demo programmers since the late 1990s.
In 1999 a team from the University of Utah, led by Steven Parker, demonstrated interactive ray tracing live at the 1999 Symposium on Interactive 3D Graphics. They rendered a 35 million sphere model at 512 by 512 pixel resolution, running at approximately 15 frames per second on 60 CPUs.
The Open RT project included a highly optimized software core for ray tracing along with an OpenGL-like API in order to offer an alternative to the current rasterization based approach for interactive 3-D graphics. Ray tracing hardware, such as the experimental Ray Processing Unit developed by Sven Woop at the Saarland University, was designed to accelerate some of the computationally intensive operations of ray tracing.
The idea that video games could ray trace their graphics in real time received media attention in the late 2000s. During that time, a researcher named Daniel Pohl, under the guidance of graphics professor Philipp Slusallek and in cooperation with the Erlangen University and Saarland University in Germany, equipped Quake III and Quake IV with an engine he programmed himself, which Saarland University then demonstrated at CeBIT 2007. Intel, a patron of Saarland, became impressed enough that it hired Pohl and embarked on a research program dedicated to ray traced graphics, which it saw as justifying increasing the number of its processors' cores. On June 12, 2008, Intel demonstrated a special version of Enemy Territory: Quake Wars, titled Quake Wars: Ray Traced, using ray tracing for rendering, running in basic HD (720p) resolution. ETQW operated at 14–29 frames per second on a 16-core (4 socket, 4 core) Xeon Tigerton system running at 2.93 GHz.
At SIGGRAPH 2009, Nvidia announced OptiX, a free API for real-time ray tracing on Nvidia GPUs. The API exposes seven programmable entry points within the ray tracing pipeline, allowing for custom cameras, ray-primitive intersections, shaders, shadowing, etc. This flexibility enables bidirectional path tracing, Metropolis light transport, and many other rendering algorithms that cannot be implemented with tail recursion. OptiX-based renderers are used in Autodesk Arnold, Adobe AfterEffects, Bunkspeed Shot, Autodesk Maya, 3ds max, and many other renderers.
In 2014, a demo of the PlayStation 4 video game The Tomorrow Children, developed by Q-Games and Japan Studio, demonstrated new lighting techniques developed by Q-Games, notably cascaded voxel cone ray tracing, which simulates lighting in real-time and uses more realistic reflections rather than screen space reflections.
Nvidia introduced their GeForce RTX and Quadro RTX GPUs September 2018, based on the Turing architecture that allows for hardware-accelerated ray tracing. The Nvidia hardware uses a separate functional block, publicly called an "RT core". This unit is somewhat comparable to a texture unit in size, latency, and interface to the processor core. The unit features BVH traversal, compressed BVH node decompression, ray-AABB intersection testing, and ray-triangle intersection testing. The GeForce RTX, in the form of models 2080 and 2080 Ti, became the first consumer-oriented brand of graphics card that can perform ray tracing in real time, and, in November 2018, Electronic Arts' Battlefield V became the first game to take advantage of its ray tracing capabilities, which it achieves via Microsoft's new API, DirectX Raytracing. AMD, which already offered interactive ray tracing on top of OpenCL through its Radeon ProRender, unveiled in October 2020 the Radeon RX 6000 series, its second generation Navi GPUs with support for hardware-accelerated ray tracing at an online event. Subsequent games that render their graphics by such means appeared since, which has been credited to the improvements in hardware and efforts to make more APIs and game engines compatible with the technology. Current home gaming consoles implement dedicated ray tracing hardware components in their GPUs for real-time ray tracing effects, which began with the ninth-generation consoles PlayStation 5, Xbox Series X and Series S.
On 4 November, 2021, Imagination Technologies announced their IMG CXT GPU with hardware-accelerated ray tracing. On January 18, 2022, Samsung announced their Exynos 2200 AP SoC with hardware-accelerated ray tracing. On June 28, 2022, Arm announced their Immortalis-G715 with hardware-accelerated ray tracing. On November 16, 2022, Qualcomm announced their Snapdragon 8 Gen 2 with hardware-accelerated ray tracing.
On September 12, 2023 Apple introduced hardware-accelerated ray tracing in its chip designs, beginning with the A17 Pro chip for iPhone 15 Pro models. Later the same year, Apple released M3 family of processors with HW enabled ray tracing support. Currently, this technology is accessible across iPhones, iPads, and Mac computers via the Metal API. Apple reports up to a 4x performance increase over previous software-based ray tracing on the phone and up to 2.5x faster comparing M3 to M1 chips. The hardware implementation includes acceleration structure traversal and dedicated ray-box intersections, and the API supports RayQuery (Inline Ray Tracing) as well as RayPipeline features.
Computational complexity
Various complexity results have been proven for certain formulations of the ray tracing problem. In particular, if the decision version of the ray tracing problem is defined as follows – given a light ray's initial position and direction and some fixed point, does the ray eventually reach that point, then the referenced paper proves the following results:
- Ray tracing in 3-D optical systems with a finite set of reflective or refractive objects represented by a system of rational quadratic inequalities is undecidable.
- Ray tracing in 3-D optical systems with a finite set of refractive objects represented by a system of rational linear inequalities is undecidable.
- Ray tracing in 3-D optical systems with a finite set of rectangular reflective or refractive objects is undecidable.
- Ray tracing in 3-D optical systems with a finite set of reflective or partially reflective objects represented by a system of linear inequalities, some of which can be irrational is undecidable.
- Ray tracing in 3-D optical systems with a finite set of reflective or partially reflective objects represented by a system of rational linear inequalities is PSPACE-hard.
- For any dimension equal to or greater than 2, ray tracing with a finite set of parallel and perpendicular reflective surfaces represented by rational linear inequalities is in PSPACE.
Software architecture
Middleware
API
See also
- Beam tracing
- Cone tracing
- Distributed ray tracing
- Global illumination
- Gouraud shading
- List of ray tracing software
- Parallel computing
- Path tracing
- Phong shading
- Progressive meshes
- Shading
- Specular reflection
- Tessellation
- Per-pixel lighting
References
- Shirley, Peter (July 9, 2003). Realistic Ray Tracing. A K Peters/CRC Press; 2nd edition. ISBN 978-1568814612.
- "Sponsored Feature: Changing the Game - Experimental Cloud-Based Ray Tracing". www.gamasutra.com. Retrieved March 18, 2021.
- "Disney explains why its 2D animation looks so realistic". Engadget. Retrieved March 18, 2021.
- "The Next Big Steps In Game Sound Design". www.gamasutra.com. January 28, 2010. Retrieved March 18, 2021.
- Georg Rainer Hofmann (1990). "Who invented ray tracing?". The Visual Computer. 6 (3): 120–124. doi:10.1007/BF01911003. S2CID 26348610..
- Steve Luecking (2013). "Dürer, drawing, and digital thinking - 2013 FATE Conference". brian-curtis.com. Retrieved August 13, 2020.
- Steve Luecking. "Stephen J Luecking". Retrieved August 13, 2020.
- Appel, Arthur (April 30, 1968). "Some techniques for shading machine renderings of solids". Proceedings of the April 30--May 2, 1968, spring joint computer conference on - AFIPS '68 (Spring) (PDF). pp. 37–45. doi:10.1145/1468075.1468082. S2CID 207171023.
- Goldstein, Robert; Nagel, Roger (January 1971), "3-D Visual simulation", Simulation, 16 (1): 25–31, doi:10.1177/003754977101600104, S2CID 122824395
- Syntha Vision Sampler. 1974 – via Internet Archive.
- Roth, Scott D. (February 1982), "Ray Casting for Modeling Solids", Computer Graphics and Image Processing, 18 (2): 109–144, doi:10.1016/0146-664X(82)90169-1
- Whitted T. (1979) An Improved Illumination Model for Shaded Display. Proceedings of the 6th annual conference on Computer graphics and interactive techniques
- The Compleat Angler. Bell Laboratories. 1978 – via Internet Archive.
- "Food for Laughs". Computer Graphics World.
- M.s (May 28, 2013). "This Animated Life: Pixar's Lightspeed Brings New Light to Monsters University". This Animated Life. Retrieved May 26, 2020.
- Hart, John C. (June 1995), "Sphere Tracing: A Geometric Method for the Antialiased Ray Tracing of Implicit Surfaces" (PDF), The Visual Computer
- Hart, John C.; Sandin, Daniel J.; Kauffman, Louis H. (July 1989), "Ray Tracing Deterministic 3-D Fractals" (PDF), Computer Graphics, 23 (3): 289–296, doi:10.1145/74334.74363
- Tomas Nikodym (June 2010). "Ray Tracing Algorithm For Interactive Applications" (PDF). Czech Technical University, FEE. Archived from the original (PDF) on March 3, 2016.
- Whitted, T. (1979). "An Improved Illumination Model for Shaded Display". Proceedings of the 6th annual conference on Computer graphics and interactive techniques. CiteSeerX 10.1.1.156.1534. ISBN 0-89791-004-4.
- Chalmers, A.; Davis, T.; Reinhard, E. (2002). Practical Parallel Rendering. AK Peters. ISBN 1-56881-179-9.
- Aila, Timo; Laine, Samulii (2009). "Understanding the Efficiency of Ray Traversal on GPUs". HPG '09: Proceedings of the Conference on High Performance Graphics 2009. pp. 145–149. doi:10.1145/1572769.1572792. ISBN 9781605586038. S2CID 15392840.
- Eric P. Lafortune and Yves D. Willems (December 1993). "Bi-Directional Path Tracing". Proceedings of Compugraphics '93: 145–153.
- Péter Dornbach (1998). "Implementation of bidirectional ray tracing algorithm" (PDF). Retrieved June 11, 2008.
- Global Illumination using Photon Maps Archived 2008-08-08 at the Wayback Machine
- "Photon Mapping - Zack Waters".
- Veach, Eric; Guibas, Leonidas J. (1997). "Metropolis Light Transport". SIGGRAPH '97: Proceedings of the 24th annual conference on Computer graphics and interactive techniques. pp. 65–76. doi:10.1145/258734.258775. ISBN 0897918967. S2CID 1832504.
- Hall, Roy A.; Greenberg, Donald P. (November 1983). "A Testbed for Realistic Image Synthesis". IEEE Computer Graphics and Applications. 3 (8): 10–20. CiteSeerX 10.1.1.131.1958. doi:10.1109/MCG.1983.263292. S2CID 9594422.
- "【Osaka University 】 LINKS-1 Computer Graphics System". IPSJ Computer Museum. Information Processing Society of Japan. Retrieved November 15, 2018.
- Defanti, Thomas A. (1984). Advances in computers. Volume 23 (PDF). Academic Press. p. 121. ISBN 0-12-012123-9.
- See Proceedings of 4th Computer Graphics Workshop, Cambridge, MA, USA, October 1987. Usenix Association, 1987. pp 86–98.
- "About BRL-CAD". Archived from the original on September 1, 2009. Retrieved January 18, 2019.
- Piero Foscari. "The Realtime Raytracing Realm". ACM Transactions on Graphics. Retrieved September 17, 2007.
- Parker, Steven; Martin, William (April 26, 1999). "Interactive ray tracing". Proceedings of the 1999 symposium on Interactive 3-D graphics. I3D '99. Vol. 5. pp. 119–126. CiteSeerX 10.1.1.6.8426. doi:10.1145/300523.300537. ISBN 1581130821. S2CID 4522715. Retrieved October 30, 2019.
- Mark Ward (March 16, 2007). "Rays light up life-like graphics". BBC News. Retrieved September 17, 2007.
- Peddie, Jon (2019). Ray Tracing: A Tool for All. Springer Nature Switzerland. ISBN 978-3-030-17490-3. Retrieved November 2, 2022.
- Abi-Chahla, Fedy (July 22, 2009). "When Will Ray Tracing Replace Rasterization?". Tom's Hardware. Archived from the original on November 3, 2022. Retrieved November 4, 2022.
- Valich, Theo (June 12, 2008). "Intel converts ET: Quake Wars to ray tracing". TG Daily. Archived from the original on October 2, 2008. Retrieved June 16, 2008.
- Nvidia (October 18, 2009). "Nvidia OptiX". Nvidia. Retrieved November 6, 2009.
- Cuthbert, Dylan (October 24, 2015). "Creating the beautiful, ground-breaking visuals of The Tomorrow Children on PS4". PlayStation Blog. Retrieved December 7, 2015.
- Kilgariff, Emmett; Moreton, Henry; Stam, Nick; Bell, Brandon (September 14, 2018). "NVIDIA Turing Architecture In-Depth". Nvidia Developer. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- Takahashi, Dean (August 20, 2018). "Nvidia unveils GeForce RTX graphics chips for real-time ray tracing games". VentureBeat. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- Chacos, Brad (November 14, 2018). "RTX on! Battlefield V becomes the first game to support DXR real-time ray tracing". PCWorld. Archived from the original on November 13, 2022. Retrieved November 13, 2018.
- "Real-Time Ray Tracing with Radeon ProRender". GPUOpen. March 20, 2018. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- Harada, Takahiro (November 23, 2020). "Hardware-Accelerated Ray Tracing in AMD Radeon™ ProRender 2.0". GPUOpen. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- Garreffa, Anthony (September 9, 2020). "AMD to reveal next-gen Big Navi RDNA 2 graphics cards on October 28". TweakTown. Retrieved September 9, 2020.
- Lyles, Taylor (September 9, 2020). "AMD's next-generation Zen 3 CPUs and Radeon RX 6000 'Big Navi' GPU will be revealed next month". The Verge. Retrieved September 10, 2020.
- "AMD Teases Radeon RX 6000 Card Performance Numbers: Aiming For 3080?". anandtech.com. AnandTech. October 8, 2020. Retrieved October 25, 2020.
- "AMD Announces Ryzen "Zen 3" and Radeon "RDNA2" Presentations for October: A New Journey Begins". anandtech.com. AnandTech. September 9, 2020. Retrieved October 25, 2020.
- Judd, Will (October 28, 2020). "AMD unveils three Radeon 6000 graphics cards with ray tracing and RTX-beating performance". Eurogamer. Retrieved October 28, 2020.
- Marrs, Adam; Shirley, Peter; Wald, Ingo (2021). Ray Tracing Gems II: Next Generation Real-Time Rendering with DXR, Vulkan, and OptiX. Apress. pp. 213–214, 791–792. hdl:20.500.12657/50334. ISBN 9781484271858.
- Warren, Tom (June 8, 2019). "Microsoft hints at next-generation Xbox 'Scarlet' in E3 teasers". The Verge. Retrieved October 8, 2019.
- Chaim, Gartenberg (October 8, 2019). "Sony confirms PlayStation 5 name, holiday 2020 release date". The Verge. Retrieved October 8, 2019.
- Warren, Tom (February 24, 2020). "Microsoft reveals more Xbox Series X specs, confirms 12 teraflops GPU". The Verge. Retrieved February 25, 2020.
- Warren, Tom (September 9, 2020). "Microsoft reveals Xbox Series S specs, promises four times the processing power of Xbox One". The Verge. Retrieved September 9, 2020.
- Vandervell, Andy (January 4, 2020). "Making sense of the rampant Xbox Series X rumour mill". Wired. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- 93digital (November 4, 2021). "Imagination launches the most advanced ray tracing GPU". Imagination. Retrieved September 17, 2023.
{{cite web}}: CS1 maint: numeric names: authors list (link) - "Ray Tracing". Imagination. Retrieved September 17, 2023.
- "Samsung Introduces Game Changing Exynos 2200 Processor With Xclipse GPU Powered by AMD RDNA 2 Architecture". news.samsung.com. Retrieved September 17, 2023.
- "Gaming Performance Unleashed with Arm's new GPUs - Announcements - Arm Community blogs - Arm Community". community.arm.com. June 28, 2022. Retrieved September 17, 2023.
- "Snapdragon 8 Gen 2 Defines a New Standard for Premium Smartphones". www.qualcomm.com. Retrieved September 17, 2023.
- "New, Snapdragon 8 Gen 2: 8 extraordinary mobile experiences, unveiled". www.qualcomm.com. Retrieved September 17, 2023.
- Bonshor, Ryan Smith, Gavin. "The Apple 2023 Fall iPhone Event Live Blog (Starts at 10am PT/17:00 UTC)". www.anandtech.com. Retrieved September 17, 2023.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ "Apple unveils iPhone 15 Pro and iPhone 15 Pro Max". Apple Newsroom. Retrieved October 27, 2024.
- ^ "Apple unveils M3, M3 Pro, and M3 Max, the most advanced chips for a personal computer". Apple Newsroom. Retrieved October 27, 2024.
- "Discover ray tracing with Metal - WWDC20 - Videos". Apple Developer. Retrieved October 27, 2024.
- "Computability and Complexity of Ray Tracing" (PDF). CS.Duke.edu.
External links
- Interactive Ray Tracing: The replacement of rasterization?
- The Compleat Angler (1978)
- Writing a Simple Ray Tracer (scratchapixel) Archived February 28, 2015, at the Wayback Machine
- Ray tracing a torus
- Ray Tracing in One Weekend Book Series
- Ray Tracing with Voxels - Part 1
| Computer graphics | |||
|---|---|---|---|
| Vector graphics | |||
| 2D graphics |
| ||
| 3D graphics | |||
| Concepts | |||
| Graphics software | |||
| Algorithms | |||
 eye position
eye position target position
target position

 numbers of square pixels on viewport vertical and horizontal direction
numbers of square pixels on viewport vertical and horizontal direction numbers of actual pixel
numbers of actual pixel vertical vector which indicates where is up and down, usually
vertical vector which indicates where is up and down, usually  -
- 
 which allows us to find the line going from eye
which allows us to find the line going from eye  through that pixel and finally get the ray described by point
through that pixel and finally get the ray described by point  (or its normalisation
(or its normalisation  ). First we need to find the coordinates of the bottom left viewport pixel
). First we need to find the coordinates of the bottom left viewport pixel  and find the next pixel by making a shift along directions parallel to viewport (vectors
and find the next pixel by making a shift along directions parallel to viewport (vectors  i
i  ) multiplied by the size of the pixel. Below we introduce formulas which include distance
) multiplied by the size of the pixel. Below we introduce formulas which include distance  between the eye and the viewport. However, this value will be reduced during ray normalization
between the eye and the viewport. However, this value will be reduced during ray normalization  and remove it from calculations).
and remove it from calculations).
 and vectors
and vectors  which are parallel to the viewport (all depicted on above picture)
which are parallel to the viewport (all depicted on above picture)


 , next we calculate viewport sizes
, next we calculate viewport sizes  divided by 2 including inverse
divided by 2 including inverse 

 along directions parallel to viewport (
along directions parallel to viewport (

 and ray
and ray  so
so


 and radius
and radius  is
is

 with direction
with direction  (here
(here 
 is its distance between
is its distance between  and
and 
 for simplicity; then
for simplicity; then





 are the points where the ray intersects the sphere.
are the points where the ray intersects the sphere.

 is the intersection point found before. The reflection direction can be found by a
is the intersection point found before. The reflection direction can be found by a  , that is
, that is

