In computer vision, rigid motion segmentation is the process of separating regions, features, or trajectories from a video sequence into coherent subsets of space and time. These subsets correspond to independent rigidly moving objects in the scene. The goal of this segmentation is to differentiate and extract the meaningful rigid motion from the background and analyze it. Image segmentation techniques labels the pixels to be a part of pixels with certain characteristics at a particular time. Here, the pixels are segmented depending on its relative movement over a period of time i.e. the time of the video sequence.
There are a number of methods that have been proposed to do so. There is no consistent way to classify motion segmentation due to its large variation in literature. Depending on the segmentation criterion used in the algorithm it can be broadly classified into the following categories: image difference, statistical methods, wavelets, layering, optical flow and factorization. Moreover, depending on the number of views required the algorithms can be two or multi view-based. Rigid motion segmentation has found an increase in its application over the recent past with rise in surveillance and video editing. These algorithms are discussed further.
Introduction to rigid motion
In general, motion can be considered to be a transformation of an object in space and time. If this transformation preserves size and shape of the object it is known as a Rigid Transformation. Rigid transform can be rotational, translational or reflective. We define rigid transformation mathematically as:

where F is a rigid transform if and only if it preserves isometry and space orientation.
In the sense of motion, rigid transform is the movement of a rigid object in space. As shown in Figure 1: this 3-D motion is the transformation from original co-ordinates (X,Y,Z) to transformed co-ordinates (X',Y',Z') which is a result of rotation and translation captured by rotational matrix R and translational vector T respectively. Hence the transform will be:
where,
has 9 unknowns which correspond to the rotational angle with each axis and has 3 unknowns () which account for translation in X,Y and Z directions respectively. This motion (3-D) in time when captured by a camera (2-D) corresponds to change of pixels in the subsequent frames of the video sequence. This transformation is also known as 2-D rigid body motion or the 2-D Euclidean transformation. It can be written as:
where,
X→ original pixel co-ordinate.
X'→ transformed pixel co-ordinate.
R→ orthonormal rotation matrix with R ⋅ R = I and |R| = 1.
t→ translational vector but in the 2D image space.
To visualize this consider an example of a video sequence of a traffic surveillance camera. It will have moving cars and this movement does not change their shape and size. Moreover, the movement is a combination of rotation and transformation of the car in 3D which is reflected in its subsequent video frames. Thus the car is said to have a rigid motion.
Motion segmentation
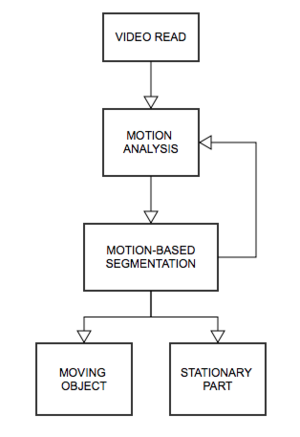
Image segmentation techniques are interested in segmenting out different parts of the image as per the region of interest. As videos are sequences of images, motion segmentation aims at decomposing a video in moving objects and background by segmenting the objects that undergo different motion patterns. The analysis of these spatial and temporal changes occurring in the image sequence by separating visual features from the scenes into different groups lets us extract visual information. Each group corresponds to the motion of an object in the dynamic sequence. In the simplest case motion segmentation can mean extracting moving objects from a stationary camera but the camera can also move which introduces the relative motion of the static background. Depending upon the type of visual features that are extracted, motion segmentation algorithms can be broadly divided into two categories. The first is known as direct motion segmentation that uses pixel intensities from the image. Such algorithms assume constant illumination. The second category of algorithms computes a set of features corresponding to actual physical points on the objects. These sparse features are then used to characterize either the 2-D motion of the scene or the 3-D motion of the objects in the scene. There are a number of requirements to design a good motion segmentation algorithm. The algorithm must extract distinct features (corners or salient points) that represent the object by a limited number of points and it must have the ability to deal with occlusions. The images will also be affected by noise and will have missing data, thus they must be robust. Some algorithms detect only one object but the video sequence may have different motions. Thus the algorithm must be multiple object detectors. Moreover, the type of camera model, if used, also characterizes the algorithm. Depending upon the object characterization of an algorithm it can detect rigid, non-rigid motion or both. Moreover, algorithms used to estimate single rigid-body motions can provide accurate results with robustness to noise and outliers but when extended to multiple rigid-body motions they fail. In case of view-based segmentation techniques described below, this happens because the single fundamental matrix assumption is violated as each motion will now be represented by means of a new fundamental matrix corresponding to that motion.
Segmentation algorithms
As mentioned earlier that there is no particular way to distinguish Motion Segmentation techniques but depending on the basis of the segmentation criterion used in the algorithm it can be broadly classified as follows:
Image difference
It is a very useful technique for detecting changes in images due to its simplicity and ability to deal with occlusion and multiple motions. These techniques assume constant light source intensity. The algorithm first considers two frames at a time and then computes the pixel by pixel intensity difference. On this computation it thresholds the intensity difference and maps the changes onto a contour. Using this contour it extracts the spatial and temporal information required to define the motion in the scene. Though it is a simple technique to implement it is not robust to noise. Another difficulty with these techniques is the camera movement. When the camera moves there is a change in the entire image which has to be accounted for. Many new algorithm have been introduced to overcome these difficulties.
Statistic theory
Motion segmentation can be seen as a classification problem where each pixel has to be classified as background or foreground. Such classifications are modeled under statistic theory and can be used in segmentation algorithms. These approaches can be further divided depending on the statistical framework used. Most commonly used frameworks are maximum a posteriori probability (MAP), Particle Filter (PF) and Expectation Maximization (EM). MAP uses Bayes' Rule for implementation where a particular pixel has to be classified under predefined classes. PF is based on the concept of evolution of a variable with varying weights over time. The final estimation is the weighted sum of all the variables. Both of these methods are iterative. The EM algorithm is also an iterative estimation method. It computes the maximum likelihood (ML) estimate of the model parameters in presence of missing or hidden data and decided the most likely fit of the observed data.
Optical Flow
Optical flow (OF) helps in determining the relative pixel velocity of points within an image sequence. Like image difference, it is also an old concept used for segmentation. Initially the main drawback of OF was the lack of robustness to noise and high computational costs but due to recent key-point matching techniques and hardware implementations, these limitations have diminished. To increase its robustness to occlusion and temporal stopping, OF is generally used with other statistical or image difference techniques. For complicated scenarios, particularly when the camera itself is moving, OF provides a basis for estimating the fundamental matrix where outliers represent other objects moving independently in the scene. Alternatively, optical flow based on line segments instead of point features can also be used to segment multiple rigid-body motions.
Wavelet
An image is made up of different frequency components. Edges, corners and plane regions can be represented by means of different frequencies. Wavelet based methods perform analysis of the different frequency components of the images and then study each component with different resolution such that they are matched to its scale. Multi-scale decomposition is used generally in order to reduce the noise. Though this method provides good results, it is limited with an assumption that the movement of objects is only in front of the camera. Implementations of Wavelet-based techniques are present with other approaches, such as optical flow and are applied at various scale to reduce the effect of noise.
Layers
Layers based techniques divide the images into layers that have uniform motion. This approach determines the different depth layer in the image and finds which layer the object or part of the image lies in. Such techniques are used in stereo vision where it is needed to compute the depth distance. The first layer based technique was proposed in 1993. As humans also use layer based segmentation, this method is a natural solution to occlusion problems but it is very complex with requirement of manual tuning.
Factorization
Tomasi and Kanade introduced the first factorization method. This method tracked features in a sequence of images and recovered the shape and motion. This technique factorized the trajectory matrix W, determined after the tracking of different features over the sequence into two matrices: motion and structure using Singular Value Decomposition. The simplicity of the algorithm is the reason for its wide use but they are sensitive to noise and outliers. Most of these methods are implemented under the assumption of rigid and independent motion.
View based algorithms
Further motion detection algorithms can also be classified depending upon the number of views: two and multi view-based approaches namely. The two-view based approaches are usually based on epipolar geometry. Consider two perspective camera views of a rigid body and find its feature correspondences. These correspondences are seen to satisfy either an epipolar constraint for a general rigid-body or a homography constraint for a planar object. Planar motion in a sequence is the motion of the background, facade or the ground. Thus it is a degenerate case of rigid body motion together with general rigid body objects e.g. cars. Hence in a sequence we expect to see more than one type of motion, described by multiple epipolar constraints and homographies. The view based algorithms are sensitive to outliers but recent approaches deal with outliers by using random sample consensus (RANSAC) and enhanced Dirichlet process mixture models. Other approaches use global dimension minimization to reveal the clusters corresponding to the underlying subspace. These approaches use only two frames for motion segmentation even if multiple frames are available as they cannot use multi frame information. Multiview-based approaches utilize the trajectory of feature points unlike two-view based approaches. A number of approaches have been provided which include Principle Angles Configuration (PAC) and Sparse Subspace Clustering (SSC) methods. These work well in two or three motion cases. These algorithms are also robust to noise with a tradeoff with speed, i.e. they are less sensitive to noise but slow in computation. Other algorithms with a multi-view approach are spectral curvature clustering (SCC), latent low-rank representation-based method (LatLRR) and ICLM-based approaches. These algorithms are faster and more accurate than the two-view based but require greater number of frames to maintain the accuracy.
Problems

Motion segmentation is a field under research as there are many issues which provide scope of improvement. One of the major problems is of feature detection and finding correspondences. There are strong feature detection algorithms but they still give false positives which can lead to unexpected correspondences. Finding these pixel or feature correspondences is a difficult task. These mismatched feature points from the objects and the background often introduce outliers. The presence of image noise and outliers further affect the accuracy of structure from motion (SFM) estimation. Another issue is that of motion models or motion representations. It requires the motion to be modeled or estimated in the given model used in the algorithm. Most algorithms perform 2-D motion segmentation by assuming the motions in the scene can be modeled by 2-D affine motion models. Theoretically, this is valid because 2-D translational motion model can be represented by general affine motion model. However, such approximations in modeling can have negative consequences. The translational model has two parameters and the affine model has 6 parameters so we estimate four extra parameters. Moreover, there may not be enough data to estimate the affine motion model so the parameter estimation might be erroneous. Some of the other problems faced are:
- Prior knowledge about the objects or about the number of objects in the scene is essential and it is not always available.
- Blurring is a common issue when motion is involved.
- Moving objects can create occlusions, and it is possible that the whole object can disappear and reappear in the scene.
- Measurement of 3-D feature correspondences in the images can be noisy in terms of pixel coordinates.
Robust algorithms have been proposed to take care of the outliers and implement with greater accuracy. The Tomasi and Kanade factorization method is one of the methods as mentioned above under factorization.
Applications
Motion segmentation has many important applications. It is used for video compression. With segmentation, it is possible to eliminate the redundancy related to the repetition of the same visual patterns in successive images. It can also be used for video description tasks, such as logging, annotation and indexing. By using Automatic object extraction techniques video content with object-specific information can be segregated. Thus concept can be used by search engines and video libraries. Some specific applications include:
- Video surveillance in security applications
- Sports scene analysis
- Road safety applications in intelligent vehicles
- Video indexing
- Traffic monitoring
- Object recognition
External links
- Vision Lab covers GPCA, RANSAC (RANdom SAmple Consensus) and Local Subspace Affinity (LSA), JCAS (Joint Categorization and Segmentation), Low-Rank Subspace Clustering (LRSC) and Sparse Representation Theory. A link to a few implementations using Matlab by the Vision Lab at The Johns Hopkins University
References
- ^ Perera, Samunda. "Rigid Body Motion Segmentation with an RGB-D Camera" (PDF).
- Zappella, Luca; Lladó, Xavier; Salvi, Joaquim (2008). "Motion Segmentation: a Review". Proceedings of the 2008 Conference on Artificial Intelligence Research and Development: Proceedings of the 11th International Conference of the Catalan Association for Artificial Intelligence Pages 398-407. IOS Press. pp. 398–407. ISBN 9781586039257.
- ^ Bewley, Alex; Guizilini, Vitor; Ramos, Fabio; Upcroft, Ben (2014). "Online self-supervised multi-instance segmentation of dynamic objects" (PDF). 2014 IEEE International Conference on Robotics and Automation (ICRA) (PDF). pp. 1296–1303. doi:10.1109/ICRA.2014.6907020. ISBN 978-1-4799-3685-4. S2CID 5907733.
- Chen, Chen-Yuan; Lin, Jeng-Wen; Lee, Wan-I; Chen, Cheng-Wu (2010). "Fuzzy Control for an Oceanic Structure: A Case Study in Time-delay TLP System". Journal of Vibration and Control.
- Cavallaro, Andrea; Steiger, Olivier; Ebrahimi, Touradj (4 April 2005). "Tracking Video Objects in Cluttered Back- ground" (PDF). IEEE Transactions on Circuits and Systems for Video Technology. 15 (4): 575–584. CiteSeerX 10.1.1.464.7218. doi:10.1109/tcsvt.2005.844447. S2CID 15604489.
- Li, Renjie; Yu, Songyu; Yang, Xiaokang (Aug 2007). "Efficient Spatio-temporal Segmentation for Extracting Moving Objects in Video Sequences". IEEE Transactions on Consumer Electronics. 53 (3): 1161–1167. CiteSeerX 10.1.1.227.6442. doi:10.1109/tce.2007.4341600. S2CID 2216371.
- Shen, Huanfeng; Zhang, Liangpei; Huang, Bo; Li, Pingxiang (February 2007). "A map approach for joint motion estimation, segmentation, and super resolution" (PDF). IEEE Transactions on Image Processing. 16 (2): 479–490. Bibcode:2007ITIP...16..479S. CiteSeerX 10.1.1.692.4884. doi:10.1109/tip.2006.888334. PMID 17269640. S2CID 14221962.
- Rathi, Y.; Vaswani, N.; Tannenbaum, A.; Yezzi, A. (2005). "Particle Filtering for Geometric Active Contours with Application to Tracking Moving and Deforming Objects" (PDF). 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Vol. 2. pp. 2–9. CiteSeerX 10.1.1.550.156. doi:10.1109/CVPR.2005.271. ISBN 978-0-7695-2372-9. S2CID 2169573.
- Liu, Guangcan; Lin, Zhouchen; Yu, Yong (2010). "Robust Subspace Segmentation by Low-Rank Representation" (PDF). Proceedings of the 27th International Conference on Machine Learning (ICML-10). Archived from the original (PDF) on 2010-07-14.
- Zhang, Jing; Shi, Fanhuai; Wang, Jianhua; Liu, Yuncai (2007). "3D Motion Segmentation from Straight-Line Optical Flow". Multimedia Content Analysis and Mining. Lecture Notes in Computer Science. Vol. 4577. Springer Berlin Heidelberg. pp. 85–94. doi:10.1007/978-3-540-73417-8_15. ISBN 978-3-540-73417-8.
- Gonzalez (1993). Digital image processing. Wesley Publishing Company. ISBN 9780201600780.
- Krüger, Volker; Feris, Rogerio S. (2001). "Wavelet Subspace Method for Real-Time Face Tracking". Pattern Recognition. Lecture Notes in Computer Science. Vol. 2191. pp. 186–193. CiteSeerX 10.1.1.18.2433. doi:10.1007/3-540-45404-7_25. ISBN 978-3-540-42596-0.
- Wang, J.Y.A.; Adelson, E.H. (1993). "Layered representation for motion analysis". Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. pp. 361–366. doi:10.1109/CVPR.1993.341105. ISBN 978-0-8186-3880-0. S2CID 5556692.
- TOMASI, CARLO; KANADE, TAKEO (1992). "Shape and Motion from Image Streams under Orthography: a Factorization Method" (PDF). International Journal of Computer Vision. 9 (2): 137–154. CiteSeerX 10.1.1.131.9807. doi:10.1007/bf00129684. S2CID 2931825.
- Rao, Shankar R; Yang, Allen Y; Sastry, S. Shanka (January 2010). "Robust Algebraic Segmentation of Mixed Rigid-Body and Planar Motions from Two Views" (PDF). Int J Comput Vis. 88 (3): 425–446. doi:10.1007/s11263-009-0314-1. S2CID 8343951.
- Fischler, Martin A.; Bolles, Robert C. (June 1981). "Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography". Communications of the ACM. 24 (6): 381–395. doi:10.1145/358669.358692. S2CID 972888.
- Chen, Chu-Song; Jian, Yong-Dian (16 January 2010). "Two-View Motion Segmentation with Model Selection and Outlier Removal by RANSAC-Enhanced Dirichlet Process Mixture Models" (PDF).
{{cite journal}}: Cite journal requires|journal=(help) - Jung, Heechul; Ju, Jeongwoo; Kim, Junmo. "Rigid Motion Segmentation using Randomized Voting" (PDF).
{{cite journal}}: Cite journal requires|journal=(help) - Zappella, L.; Provenzi, E.; Lladó, X.; Salvi, J. (2011). Adaptive Motion Segmentation Algorithm Based on the Principal Angles Configuration, Computer Vision – ACCV 2010. Springer Berlin Heidelberg. pp. 15–26. ISBN 978-3-642-19318-7.
- Elhamifar, Ehsan; Vidal, Rene (2009). "Sparse subspace clustering". 2009 IEEE Conference on Computer Vision and Pattern Recognition. pp. 2790–2797. CiteSeerX 10.1.1.217.953. doi:10.1109/CVPR.2009.5206547. ISBN 978-1-4244-3992-8. S2CID 847078.
- Liu, Guangcan; Yan, Shuicheng (Nov 2011). "Latent Low-Rank Representation for subspace segmentation and feature extraction". 2011 International Conference on Computer Vision (PDF). pp. 1615–1622. doi:10.1109/ICCV.2011.6126422. ISBN 978-1-4577-1102-2. S2CID 6240314.
- Flores-Mangas; Jepson (June 2013). "Fast Rigid Motion Segmentation via Incrementally-Complex Local Models". 2013 IEEE Conference on Computer Vision and Pattern Recognition (PDF). pp. 2259–2266. CiteSeerX 10.1.1.692.7518. doi:10.1109/CVPR.2013.293. ISBN 978-0-7695-4989-7. S2CID 6116643.



 has 9 unknowns which correspond to the rotational angle with each axis and
has 9 unknowns which correspond to the rotational angle with each axis and  has 3 unknowns (
has 3 unknowns ( ) which account for translation in X,Y and Z directions respectively.
This motion (3-D) in time when captured by a camera (2-D) corresponds to change of pixels in the subsequent frames of the video sequence. This transformation is also known as 2-D rigid body motion or the 2-D
) which account for translation in X,Y and Z directions respectively.
This motion (3-D) in time when captured by a camera (2-D) corresponds to change of pixels in the subsequent frames of the video sequence. This transformation is also known as 2-D rigid body motion or the 2-D 
