The Sleeping Beauty problem, also known as the Sleeping Beauty paradox, is a puzzle in decision theory in which an ideally rational epistemic agent is told she will be awoken from sleep either once or twice according to the toss of a coin. Each time she will have no memory of whether she has been awoken before, and is asked what her degree of belief that “the outcome of the coin toss is Heads” ought to be when she is first awakened.
History
The problem was originally formulated in unpublished work in the mid-1980s by Arnold Zuboff (the work was later published as "One Self: The Logic of Experience") followed by a paper by Adam Elga. A formal analysis of the problem of belief formation in decision problems with imperfect recall was provided first by Michele Piccione and Ariel Rubinstein in their paper: "On the Interpretation of Decision Problems with Imperfect Recall" where the "paradox of the absent minded driver" was first introduced and the Sleeping Beauty problem discussed as Example 5. The name "Sleeping Beauty" was given to the problem by Robert Stalnaker and was first used in extensive discussion in the Usenet newsgroup rec.puzzles in 1999.
The problem
As originally published by Elga, the problem was:
- Some researchers are going to put you to sleep. During the two days that your sleep will last, they will briefly wake you up either once or twice, depending on the toss of a fair coin (Heads: once; Tails: twice). After each waking, they will put you back to sleep with a drug that makes you forget that waking. When you are first awakened, to what degree ought you believe that the outcome of the coin toss is Heads?
The only significant difference from Zuboff's unpublished versions is the number of potential wakings; Zuboff used a large number. Elga created a schedule within which to implement his solution, and this has become the canonical form of the problem:
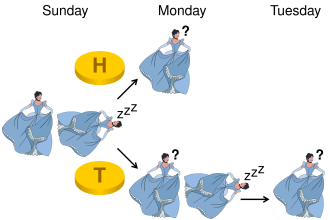
Sleeping Beauty volunteers to undergo the following experiment and is told all of the following details: On Sunday she will be put to sleep. Once or twice, during the experiment, Sleeping Beauty will be awakened, interviewed, and put back to sleep with an amnesia-inducing drug that makes her forget that awakening. A fair coin will be tossed to determine which experimental procedure to undertake:
- If the coin comes up heads, Sleeping Beauty will be awakened and interviewed on Monday only.
- If the coin comes up tails, she will be awakened and interviewed on Monday and Tuesday.
In either case, she will be awakened on Wednesday without interview and the experiment ends.
Any time Sleeping Beauty is awakened and interviewed she will not be able to tell which day it is or whether she has been awakened before. During the interview Sleeping Beauty is asked: "What is your credence now for the proposition that the coin landed heads?"
Solutions
This problem continues to produce ongoing debate.
Thirder position
The thirder position argues that the probability of heads is 1/3. Adam Elga argued for this position originally as follows: Suppose Sleeping Beauty is told and she comes to fully believe that the coin landed tails. By even a highly restricted principle of indifference, given that the coin lands tails, her credence that it is Monday should equal her credence that it is Tuesday, since being in one situation would be subjectively indistinguishable from the other. In other words, P(Monday|Tails) = P(Tuesday|Tails), and thus
- P(Tails and Tuesday) = P(Tails and Monday).
Suppose now that Sleeping Beauty is told upon awakening and comes to fully believe that it is Monday. Guided by the objective chance of heads landing being equal to the chance of tails landing, it should hold that P(Tails|Monday) = P(Heads|Monday), and thus
- P(Tails and Tuesday) = P(Tails and Monday) = P(Heads and Monday).
Since these three outcomes are exhaustive and exclusive for one trial (and thus their probabilities must add to 1), the probability of each is then 1/3 by the previous two steps in the argument.
An alternative argument is as follows: Credence can be viewed as the amount a rational risk-neutral bettor would wager if the payoff for being correct is 1 unit (the wager itself being lost either way). In the heads scenario, Sleeping Beauty would spend her wager amount one time, and receive 1 money for being correct. In the tails scenario, she would spend her wager amount twice, and receive nothing. Her expected value is therefore to gain 0.5 but also lose 1.5 times her wager, thus she should break even if her wager is 1/3.
Halfer position
David Lewis responded to Elga's paper with the position that Sleeping Beauty's credence that the coin landed heads should be 1/2. Sleeping Beauty receives no new non-self-locating information throughout the experiment because she is told the details of the experiment. Since her credence before the experiment is P(Heads) = 1/2, she ought to continue to have a credence of P(Heads) = 1/2 since she gains no new relevant evidence when she wakes up during the experiment. This directly contradicts one of the thirder's premises, since it means P(Tails|Monday) = 1/3 and P(Heads|Monday) = 2/3.
Double halfer position
The double halfer position argues that both P(Heads) and P(Heads|Monday) equal 1/2. Mikaël Cozic, in particular, argues that context-sensitive propositions like "it is Monday" are in general problematic for conditionalization and proposes the use of an imaging rule instead, which supports the double halfer position.
Ambiguous question position
Another approach to the Sleeping Beauty problem is to assert that the problem, as stated, is ambiguous. This view asserts that the thirder and halfer positions are both correct answers, but to different questions. The key idea is that the question asked of Sleeping Beauty, "what is your credence that the coin came up heads", is ambiguous. The question must be disambiguated based on the particular event whose probability we wish to measure. The two disambiguations are: "what is your credence that the coin landed heads in the act of tossing" and "what is your credence that the coin landed heads in the toss to set up this awakening"; to which, the correct answers are 1/2 and 1/3 respectively.
Another way to see the two different questions is to simplify the Sleeping Beauty problem as follows. Imagine tossing a coin, if the coin comes up heads, a green ball is placed into a box; if, instead, the coin comes up tails, two red balls are placed into a box. We repeat this procedure a large number of times until the box is full of balls of both colours. A single ball is then drawn from the box. In this setting, the question from the original problem resolves to one of two different questions: "what is the probability that a green ball was placed in the box" and "what is the probability a green ball was drawn from the box". These questions ask for the probability of two different events, and thus can have different answers, even though both events are causally dependent on the coin landing heads. (This fact is even more obvious when one considers the complementary questions: "what is the probability that two red balls were placed in the box" and "what is the probability that a red ball was drawn from the box".)
This view evidently violates the principle that, if event A happens if and only if event B happens, then we should have equal credence for event A and event B. This principle is not applicable because the sample spaces are different.
Connections to other problems
Credence about what precedes awakenings is a core question in connection with the anthropic principle.
Variations
Extreme Sleeping Beauty
This differs from the original in that there are one million and one wakings if tails comes up. It was formulated by Nick Bostrom.
Sailor's Child problem
The Sailor's Child problem, introduced by Radford M. Neal, is somewhat similar. It involves a sailor who regularly sails between ports. In one port there is a woman who wants to have a child with him, across the sea there is another woman who also wants to have a child with him. The sailor cannot decide if he will have one or two children, so he will leave it up to a coin toss. If Heads, he will have one child, and if Tails, two children (one with each woman; presumably the children will never meet). But if the coin lands on Heads, which woman would have his child? He would decide this by looking at The Sailor's Guide to Ports and the woman in the port that appears first would be the woman that he has a child with. You are his child. You do not have a copy of The Sailor's Guide to Ports. What is the probability that you are his only child, thus the coin landed on Heads (assume a fair coin)?
See also
References
- Lewis, Peter J. (2007). "Quantum Sleeping Beauty". Analysis. 67 (1): 59–65. doi:10.1093/analys/67.1.59. JSTOR 25597774.
- Arnold Zuboff (1990). "One Self: The Logic of Experience". Inquiry: An Interdisciplinary Journal of Philosophy. 33 (1): 39–68. doi:10.1080/00201749008602210.(subscription required)
- ^ Elga, A. (2000). "Self-locating Belief and the Sleeping Beauty Problem". Analysis. 60 (2): 143–147. CiteSeerX 10.1.1.32.3107. doi:10.1093/analys/60.2.143. JSTOR 3329167.
- Michele Piccione and Ariel Rubinstein (1997) “On the Interpretation of Decision Problems with Imperfect Recall,” Games and Economic Behavior 20, 3-24.
- Michele Piccione and Ariel Rubinstein (1997) “The Absent Minded Driver's Paradox: Synthesis and Responses,” Games and Economic Behavior 20, 121-130.
- Nick Wedd (June 14, 2006). "Some "Sleeping Beauty" postings". Retrieved November 7, 2014.
- Lewis, D. (2001). "Sleeping Beauty: reply to Elga" (PDF). Analysis. 61 (3): 171–76. doi:10.1093/analys/61.3.171. JSTOR 3329230.
- Meacham, C. J. (2008). "Sleeping beauty and the dynamics of de se beliefs". Philosophical Studies. 138 (2): 245–269. CiteSeerX 10.1.1.517.4904. doi:10.1007/s11098-006-9036-1. JSTOR 40208872. S2CID 26902640.
- Mikaël Cozic (February 2011). "Imaging and Sleeping Beauty: A case for double-halfers". International Journal of Approximate Reasoning. 52 (2): 137–143. doi:10.1016/j.ijar.2009.06.010.
- ^ Groisman, Berry (September 2008). "The end of Sleeping Beauty's nightmare". The British Journal for the Philosophy of Science. 59 (3): 409–416. arXiv:0806.1316. doi:10.1093/bjps/axn015.
- Mutalik, Pradeep. "Why Sleeping Beauty Is Lost in Time". Quanta Magazine. Retrieved 18 August 2023.
- Haran, Brady; Crawford, Tom. "Sleeping Beauty Paradox". Youtube. Numberphile. Retrieved 18 August 2023.
- ^ Luna, Laureano (2020-09-01). "Sleeping Beauty: Exploring a Neglected Solution" (PDF). The British Journal for the Philosophy of Science. 71 (3): 1069–1092. doi:10.1093/bjps/axy045. ISSN 0007-0882.
- Bostrom, Nick (2007). "Sleeping Beauty and Self-Location: A Hybrid Model". Synthese. 157 (1): 59–78. doi:10.1007/s11229-006-9010-7. ISSN 0039-7857. S2CID 12215640.
- Neal, Radford M. (2006). "Puzzles of Anthropic Reasoning Resolved Using Full Non-indexical Conditioning". arXiv:math/0608592.
Other works discussing the Sleeping Beauty problem
- Arntzenius, F (2002). "Reflections on Sleeping Beauty". Analysis. 62 (1): 53–62. doi:10.1093/analys/62.1.53. JSTOR 3329069.
- Bostrom, Nick (2002-07-12). Anthropic Bias. Routledge (UK). pp. 195–96. ISBN 978-0-415-93858-7.
- Bradley, D (2003). "Sleeping Beauty: a note on Dorr's argument for 1/3". Analysis. 63 (3): 266–268. doi:10.1093/analys/63.3.266. JSTOR 3329324.
- Bruce, Colin (2004-12-21). Schrodinger's Rabbits: Entering the Many Worlds of Quantum. Joseph Henry Press. pp. 193–96. ISBN 978-0-309-09051-3.
- Colombo, M., Lai, J. & Crupi, V. Sleeping Beauty Goes to the Lab: The Psychology of Self-Locating Evidence. Rev.Phil.Psych. 10, 173–185 (2019). https://doi.org/10.1007/s13164-018-0381-8
- Dorr, C (2002). "Sleeping Beauty: in Defence of Elga". Analysis. 62 (4): 292–296. doi:10.1093/analys/62.4.292. JSTOR 3328920.
- Elga, A. (2000). "Self-locating Belief and the Sleeping Beauty Problem". Analysis. 60 (2): 143–147. doi:10.1093/analys/60.2.143. JSTOR 3329167.
- Lewis, D. (2001). "Sleeping Beauty: reply to Elga" (PDF). Analysis. 61 (3): 171–76. doi:10.1093/analys/61.3.171. JSTOR 3329230.
- Meacham, C. J. (2008). "Sleeping beauty and the dynamics of de se beliefs". Philosophical Studies. 138 (2): 245–269. CiteSeerX 10.1.1.517.4904. doi:10.1007/s11098-006-9036-1. JSTOR 40208872. S2CID 26902640.
- Monton, B. (2002). "Sleeping Beauty and the Forgetful Bayesian". Analysis. 62 (1): 47–53. doi:10.1093/analys/62.1.47. JSTOR 3329068.
- Neal, R. (2006). Puzzles of Anthropic Reasoning Resolved Using Full Non-indexical Conditioning, preprint
- Rosenthal, J.S. (2009). "A mathematical analysis of the Sleeping Beauty problem". The Mathematical Intelligencer. 31 (3): 32–37. CiteSeerX 10.1.1.151.2326. doi:10.1007/s00283-009-9060-z. S2CID 14152244.
- Titelbaum, M. (2013). Quitting Certainties, 210–229, 233–237, 241–249, 250, 276–277
- Zuboff, A. (1990). "One Self: The Logic of Experience". Inquiry. 33 (1): 39–68. doi:10.1080/00201749008602210.
- Wenmackers, S. (2017). "The Snow White problem". Synthese. 196 (10): 4137–4153. doi:10.1007/s11229-017-1647-x. S2CID 255061772.
External links
- Terry Horgan: Sleeping Beauty Awakened: New Odds at the Dawn of the New Day (review paper with references)
- Franceschi, Paul. "A Two-Sided Ontological Solution to the Sleeping Beauty Problem" (PDF).
- Anthropic Preprint Archive: The Sleeping Beauty Problem: An archive of papers on this problem
- Phil Papers Entry on Sleeping Beauty (a complete bibliography of papers on the problem)
- Twoplustwo thread discussing the sleeping beauty problem in depth
- Bischoff, Manon (2023-05-04). "Why the 'Sleeping Beauty Problem' Is Keeping Mathematicians Awake". Scientific American. Retrieved 2023-05-10.