In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite-state machine. The most widely studied shift spaces are the subshifts of finite type.
Motivating examples
A (one-sided) shift of finite type is the set of all sequences, infinite on one end only, that can be made up of the letters , like . A (two-sided) shift of finite type is similar, but consists of sequences that are infinite on both ends.
A subshift can be defined by a directed graph on these letters, such as the graph . It consists of sequences whose transitions between consecutive letters are only those allowed by the graph. For this example, the subshift consists of only three one-sided sequences: . Similarly, the two-sided subshift described by this graph consists of only three two-sided sequences.
Other directed graphs on the same letters produce other subshifts. For example, adding another arrow to the graph produces a subshift that, instead of containing three sequences, contains an uncountably infinite number of sequences.
Markov and non-Markov measures
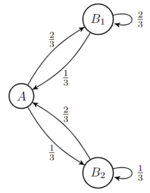
Given a Markov transition matrix and an invariant distribution on the states, we can impose a probability measure on the set of subshifts. For example, consider the Markov chain given on the left on the states , with invariant distribution . If we "forget" the distinction between , we project this space of subshifts on into another space of subshifts on , and this projection also projects the probability measure down to a probability measure on the subshifts on .
The curious thing is that the probability measure on the subshifts on is not created by a Markov chain on , not even multiple orders. Intuitively, this is because if one observes a long sequence of , then one would become increasingly sure that the , meaning that the observable part of the system can be affected by something infinitely in the past.
Conversely, there exists a space of subshifts on 6 symbols, projected to subshifts on 2 symbols, such that any Markov measure on the smaller subshift has a preimage measure that is not Markov of any order (Example 2.6 ).
Definition
Let V be a finite set of n symbols (alphabet). Let X denote the set of all bi-infinite sequences of elements of V together with the shift operator T. We endow V with the discrete topology and X with the product topology. A symbolic flow or subshift is a closed T-invariant subset Y of X and the associated language LY is the set of finite subsequences of Y.
Now let A be an n × n adjacency matrix with entries in {0, 1}. Using these elements we construct a directed graph G = (V, E) with V the set of vertices and E the set of edges containing the directed edge x → y in E if and only if Ax, y = 1. Let Y be the set of all infinite admissible sequences of edges, where by admissible it is meant that the sequence is a walk of the graph, and the sequence can be either one-sided or two-sided infinite. Let T be the left shift operator on such sequences; it plays the role of the time-evolution operator of the dynamical system. A subshift of finite type is then defined as a pair (Y, T) obtained in this way. If the sequence extends to infinity in only one direction, it is called a one-sided subshift of finite type, and if it is bilateral, it is called a two-sided subshift of finite type.
Formally, one may define the sequences of edges as
This is the space of all sequences of symbols such that the symbol p can be followed by the symbol q only if the (p, q)-th entry of the matrix A is 1. The space of all bi-infinite sequences is defined analogously:
The shift operator T maps a sequence in the one- or two-sided shift to another by shifting all symbols to the left, i.e.
Clearly this map is only invertible in the case of the two-sided shift.
A subshift of finite type is called transitive if G is strongly connected: there is a sequence of edges from any one vertex to any other vertex. It is precisely transitive subshifts of finite type which correspond to dynamical systems with orbits that are dense.
An important special case is the full n-shift: it has a graph with an edge that connects every vertex to every other vertex; that is, all of the entries of the adjacency matrix are 1. The full n-shift corresponds to the Bernoulli scheme without the measure.
Terminology
By convention, the term shift is understood to refer to the full n-shift. A subshift is then any subspace of the full shift that is shift-invariant (that is, a subspace that is invariant under the action of the shift operator), non-empty, and closed for the product topology defined below. Some subshifts can be characterized by a transition matrix, as above; such subshifts are then called subshifts of finite type. Often, subshifts of finite type are called simply shifts of finite type. Subshifts of finite type are also sometimes called topological Markov shifts.
Examples
Many chaotic dynamical systems are isomorphic to subshifts of finite type; examples include systems with transverse homoclinic connections, diffeomorphisms of closed manifolds with a positive metric entropy, the Prouhet–Thue–Morse system, the Chacon system (this is the first system shown to be weakly mixing but not strongly mixing), Sturmian systems and Toeplitz systems.
Generalizations
A sofic system is an image of a subshift of finite type where different edges of the transition graph may be mapped to the same symbol. For example, if one only watches the output from a hidden Markov chain, then the output appears to be a sofic system. It may be regarded as the set of labellings of paths through an automaton: a subshift of finite type then corresponds to an automaton which is deterministic. Such systems correspond to regular languages.
Context-free systems are defined analogously, and are generated by phrase structure grammars.
A renewal system is defined to be the set of all infinite concatenations of some fixed finite collection of finite words.
Subshifts of finite type are identical to free (non-interacting) one-dimensional Potts models (n-letter generalizations of Ising models), with certain nearest-neighbor configurations excluded. Interacting Ising models are defined as subshifts together with a continuous function of the configuration space (continuous with respect to the product topology, defined below); the partition function and Hamiltonian are explicitly expressible in terms of this function.
Subshifts may be quantized in a certain way, leading to the idea of the quantum finite automata.
Topology
A subshift has a natural topology, derived from the product topology on where
and V is given the discrete topology. A basis for the topology of which induces the topology of the subshift, is the family of cylinder sets
The cylinder sets are clopen sets in Every open set in is a countable union of cylinder sets. Every open set in the subshift is the intersection of an open set of with the subshift. With respect to this topology, the shift T is a homeomorphism; that is, with respect to this topology, it is continuous with continuous inverse.
The space is homeomorphic to a Cantor set.
Metric
A variety of different metrics can be defined on a shift space. One can define a metric on a shift space by considering two points to be "close" if they have many initial symbols in common; this is the p-adic metric. In fact, both the one- and two-sided shift spaces are compact metric spaces.
Measure
A subshift of finite type may be endowed with any one of several different measures, thus leading to a measure-preserving dynamical system. A common object of study is the Markov measure, which is an extension of a Markov chain to the topology of the shift.
A Markov chain is a pair (P, π) consisting of the transition matrix, an n × n matrix P = (pij) for which all pij ≥ 0 and
for all i. The stationary probability vector π = (πi) has all πi ≥ 0, and has
A Markov chain, as defined above, is said to be compatible with the shift of finite type if pij = 0 whenever Aij = 0. The Markov measure of a cylinder set may then be defined by
The Kolmogorov–Sinai entropy with relation to the Markov measure is
Zeta function
The Artin–Mazur zeta function is defined as the formal power series
where Fix(T) is the set of fixed points of the n-fold shift. It has a product formula
where γ runs over the closed orbits. For subshifts of finite type, the zeta function is a rational function of z:
See also
Notes
- ^ Sofic Measures: Characterizations of Hidden Markov Chains by Linear Algebra, Formal Languages, and Symbolic Dynamics - Karl Petersen, Mathematics 210, Spring 2006, University of North Carolina at Chapel Hill
- ^ Boyle, Mike; Petersen, Karl (2010-01-13), Hidden Markov processes in the context of symbolic dynamics, arXiv:0907.1858
- Xie (1996) p.21
- Xie (1996) p.22
- Matthew Nicol and Karl Petersen, (2009) "Ergodic Theory: Basic Examples and Constructions", Encyclopedia of Complexity and Systems Science, Springer https://doi.org/10.1007/978-0-387-30440-3_177
- Pytheas Fogg (2002) p.205
- ^ Brin & Stuck (2002) p.60
- Brin & Stuck (2002) p.61
References
- Brin, Michael; Stuck, Garrett (2002). Introduction to Dynamical Systems (2nd ed.). Cambridge University Press. ISBN 0-521-80841-3.
- David Damanik, Strictly Ergodic Subshifts and Associated Operators, (2005)
- Pytheas Fogg, N. (2002). Berthé, Valérie; Ferenczi, Sébastien; Mauduit, Christian; Siegel, A. (eds.). Substitutions in dynamics, arithmetics and combinatorics. Lecture Notes in Mathematics. Vol. 1794. Berlin: Springer-Verlag. ISBN 3-540-44141-7. Zbl 1014.11015.
- Natasha Jonoska, Subshifts of Finite Type, Sofic Systems and Graphs, (2000).
- Michael S. Keane, Ergodic theory and subshifts of finite type, (1991), appearing as Chapter 2 in Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Tim Bedford, Michael Keane and Caroline Series, Eds. Oxford University Press, Oxford (1991). ISBN 0-19-853390-X (Provides a short expository introduction, with exercises, and extensive references.)
- Lind, Douglas; Marcus, Brian (1995). An introduction to symbolic dynamics and coding. Cambridge University Press. ISBN 0-521-55124-2. Zbl 1106.37301.
- Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.
- Xie, Huimin (1996). Grammatical Complexity and One-Dimensional Dynamical Systems. Directions in Chaos. Vol. 6. World Scientific. ISBN 9810223986.
Further reading
- Williams, Susan G., ed. (2004). Symbolic Dynamics and Its Applications: American Mathematical Society, Short Course, January 4-5, 2002, San Diego, California. Proceedings of symposia in applied mathematics: AMS short course lecture notes. Vol. 60. American Mathematical Society. ISBN 0-8218-3157-7. Zbl 1052.37003.
 , like
, like  . A (two-sided) shift of finite type is similar, but consists of sequences that are infinite on both ends.
. A (two-sided) shift of finite type is similar, but consists of sequences that are infinite on both ends.
 . It consists of sequences whose transitions between consecutive letters are only those allowed by the graph. For this example, the subshift consists of only three one-sided sequences:
. It consists of sequences whose transitions between consecutive letters are only those allowed by the graph. For this example, the subshift consists of only three one-sided sequences:  . Similarly, the two-sided subshift described by this graph consists of only three two-sided sequences.
. Similarly, the two-sided subshift described by this graph consists of only three two-sided sequences.
 to the graph produces a subshift that, instead of containing three sequences, contains
to the graph produces a subshift that, instead of containing three sequences, contains  , with invariant distribution
, with invariant distribution  . If we "forget" the distinction between
. If we "forget" the distinction between  , we project this space of subshifts on
, we project this space of subshifts on  , and this projection also projects the probability measure down to a probability measure on the subshifts on
, and this projection also projects the probability measure down to a probability measure on the subshifts on  , then one would become increasingly sure that the
, then one would become increasingly sure that the  , meaning that the observable part of the system can be affected by something infinitely in the past.
, meaning that the observable part of the system can be affected by something infinitely in the past.
 of all bi-infinite sequences of elements of V together with the
of all bi-infinite sequences of elements of V together with the 


 where
where


 Every open set in
Every open set in 
 and has
and has





