"Barycenter" redirects here. For the general concept, see Barycenter (physics). Animation of barycenters
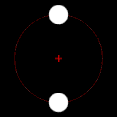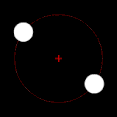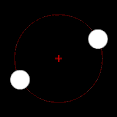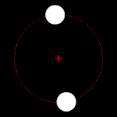 Two bodies with similar mass, like the 90 Antiope asteroid system
Two bodies with similar mass, like the 90 Antiope asteroid system Two bodies with slightly different masses, like Pluto and Charon
Two bodies with slightly different masses, like Pluto and Charon Two bodies with significant difference in masses, like Earth and the Moon
Two bodies with significant difference in masses, like Earth and the Moon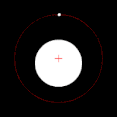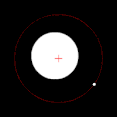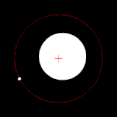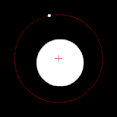 Two bodies with an extreme difference in mass, like the Sun and Earth
Two bodies with an extreme difference in mass, like the Sun and Earth Two bodies with the same mass with eccentric elliptic orbits, common for binary stars
Two bodies with the same mass with eccentric elliptic orbits, common for binary stars
| Part of a series on |
| Astrodynamics |
|---|
| Orbital mechanics |
| Orbital elements |
|
Types of two-body orbits by eccentricity Transfer orbit |
| Equations |
| Celestial mechanics |
| Gravitational influences |
| N-body orbitsLagrangian points |
| Engineering and efficiency |
| Preflight engineering |
| Efficiency measures |
| Propulsive maneuvers |
In astronomy, the barycenter (or barycentre; from Ancient Greek βαρύς (barús) 'heavy' and κέντρον (kéntron) 'center') is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important concept in fields such as astronomy and astrophysics. The distance from a body's center of mass to the barycenter can be calculated as a two-body problem.
If one of the two orbiting bodies is much more massive than the other and the bodies are relatively close to one another, the barycenter will typically be located within the more massive object. In this case, rather than the two bodies appearing to orbit a point between them, the less massive body will appear to orbit about the more massive body, while the more massive body might be observed to wobble slightly. This is the case for the Earth–Moon system, whose barycenter is located on average 4,671 km (2,902 mi) from Earth's center, which is 74% of Earth's radius of 6,378 km (3,963 mi). When the two bodies are of similar masses, the barycenter will generally be located between them and both bodies will orbit around it. This is the case for Pluto and Charon, one of Pluto's natural satellites, as well as for many binary asteroids and binary stars. When the less massive object is far away, the barycenter can be located outside the more massive object. This is the case for Jupiter and the Sun; despite the Sun being a thousandfold more massive than Jupiter, their barycenter is slightly outside the Sun due to the relatively large distance between them.
In astronomy, barycentric coordinates are non-rotating coordinates with the origin at the barycenter of two or more bodies. The International Celestial Reference System (ICRS) is a barycentric coordinate system centered on the Solar System's barycenter.
Two-body problem
Main article: Two-body problemThe barycenter is one of the foci of the elliptical orbit of each body. This is an important concept in the fields of astronomy and astrophysics. In a simple two-body case, the distance from the center of the primary to the barycenter, r1, is given by:
where :
- r1 is the distance from body 1's center to the barycenter
- a is the distance between the centers of the two bodies
- m1 and m2 are the masses of the two bodies.
The semi-major axis of the secondary's orbit, r2, is given by r2 = a − r1.
When the barycenter is located within the more massive body, that body will appear to "wobble" rather than to follow a discernible orbit.
Primary–secondary examples
The following table sets out some examples from the Solar System. Figures are given rounded to three significant figures. The terms "primary" and "secondary" are used to distinguish between involved participants, with the larger being the primary and the smaller being the secondary.
- m1 is the mass of the primary in Earth masses (ME)
- m2 is the mass of the secondary in Earth masses (ME)
- a (km) is the average orbital distance between the centers of the two bodies
- r1 (km) is the distance from the center of the primary to the barycenter
- R1 (km) is the radius of the primary
- r1/R1 a value less than one means the barycenter lies inside the primary
| Primary | m1 (ME) |
Secondary | m2 (ME) |
a (km) |
r1 (km) |
R1 (km) |
r1/R1 |
|---|---|---|---|---|---|---|---|
| Earth | 1 | Moon | 0.0123 | 384,400 | 4,670 | 6,380 | 0.732 |
| Pluto | 0.0021 | Charon | 0.000254 (0.121 M♇) |
19,600 | 2,110 | 1,150 | 1.83 |
| Sun | 333,000 | Earth | 1 | 150,000,000 (1 AU) |
449 | 696,000 | 0.000646 |
| Sun | 333,000 | Jupiter | 318 (0.000955 M☉) |
778,000,000 (5.20 AU) |
742,000 | 696,000 | 1.07 |
| Sun | 333,000 | Saturn | 95.2 | 1,430,000,000 (9.58 AU) |
409,000 | 696,000 | 0.588 |
- The Earth has a perceptible "wobble". Also see tides.
- Pluto and Charon are sometimes considered a binary system because their barycenter does not lie within either body.
- The Sun's wobble is barely perceptible.
- The Sun orbits a barycenter just above its surface.
Example with the Sun


If m1 ≫ m2—which is true for the Sun and any planet—then the ratio r1/R1 approximates to:
Hence, the barycenter of the Sun–planet system will lie outside the Sun only if:
—that is, where the planet is massive and far from the Sun.
If Jupiter had Mercury's orbit (57,900,000 km, 0.387 AU), the Sun–Jupiter barycenter would be approximately 55,000 km from the center of the Sun (r1/R1 ≈ 0.08). But even if the Earth had Eris's orbit (1.02×10 km, 68 AU), the Sun–Earth barycenter would still be within the Sun (just over 30,000 km from the center).
To calculate the actual motion of the Sun, only the motions of the four giant planets (Jupiter, Saturn, Uranus, Neptune) need to be considered. The contributions of all other planets, dwarf planets, etc. are negligible. If the four giant planets were on a straight line on the same side of the Sun, the combined center of mass would lie at about 1.17 solar radii, or just over 810,000 km, above the Sun's surface.
The calculations above are based on the mean distance between the bodies and yield the mean value r1. But all celestial orbits are elliptical, and the distance between the bodies varies between the apses, depending on the eccentricity, e. Hence, the position of the barycenter varies too, and it is possible in some systems for the barycenter to be sometimes inside and sometimes outside the more massive body. This occurs where:
The Sun–Jupiter system, with eJupiter = 0.0484, just fails to qualify: 1.05 < 1.07 > 0.954.
Relativistic corrections
In classical mechanics (Newtonian gravitation), this definition simplifies calculations and introduces no known problems. In general relativity (Einsteinian gravitation), complications arise because, while it is possible, within reasonable approximations, to define the barycenter, we find that the associated coordinate system does not fully reflect the inequality of clock rates at different locations. Brumberg explains how to set up barycentric coordinates in general relativity.
The coordinate systems involve a world-time, i.e. a global time coordinate that could be set up by telemetry. Individual clocks of similar construction will not agree with this standard, because they are subject to differing gravitational potentials or move at various velocities, so the world-time must be synchronized with some ideal clock that is assumed to be very far from the whole self-gravitating system. This time standard is called Barycentric Coordinate Time (TCB).
Selected barycentric orbital elements
Barycentric osculating orbital elements for some objects in the Solar System are as follows:
| Object | Semi-major axis (in AU) |
Apoapsis (in AU) |
Orbital period (in years) |
|---|---|---|---|
| C/2006 P1 (McNaught) | 2,050 | 4,100 | 92,600 |
| C/1996 B2 (Hyakutake) | 1,700 | 3,410 | 70,000 |
| C/2006 M4 (SWAN) | 1,300 | 2,600 | 47,000 |
| (308933) 2006 SQ372 | 799 | 1,570 | 22,600 |
| (87269) 2000 OO67 | 549 | 1,078 | 12,800 |
| 90377 Sedna | 506 | 937 | 11,400 |
| 2007 TG422 | 501 | 967 | 11,200 |
For objects at such high eccentricity, barycentric coordinates are more stable than heliocentric coordinates for a given epoch because the barycentric osculating orbit is not as greatly affected by where Jupiter is on its 11.8 year orbit.
See also
- Barycentric Dynamical Time
- Centers of gravity in non-uniform fields
- Center of mass
- Lagrange point
- Mass point geometry
- Roll center
- Weight distribution
References
- "barycentre". Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
- MacDougal, Douglas W. (December 2012). Newton's Gravity: An Introductory Guide to the Mechanics of the Universe. Berlin: Springer Science & Business Media. p. 199. ISBN 978-1-4614-5444-1.
- "Center of Gravity - an overview". ScienceDirect Topics.
barycentre lies 1700 km below the Earth's surface
(6370km–1700km) - Olkin, C. B.; Young, L. A.; Borncamp, D.; et al. (January 2015). "Evidence that Pluto's atmosphere does not collapse from occultations including the 2013 May 04 event". Icarus. 246: 220–225. Bibcode:2015Icar..246..220O. doi:10.1016/j.icarus.2014.03.026. hdl:10261/167246.
- "If You Think Jupiter Orbits the Sun, You're Mistaken". HowStuffWorks. 9 August 2016.
The Sol-Jupiter barycenter sits 1.07 times the radius of the sun
- "What's a Barycenter?". Space Place @ NASA. 8 September 2005. Archived from the original on 23 December 2010. Retrieved 20 January 2011.
- Meeus, Jean (1997), Mathematical Astronomy Morsels, Richmond, Virginia: Willmann-Bell, pp. 165–168, ISBN 0-943396-51-4
- Brumberg, Victor A. (1991). Essential Relativistic Celestial Mechanics. London: Adam Hilger. ISBN 0-7503-0062-0.
- Horizons output (30 January 2011). "Barycentric Osculating Orbital Elements for 2007 TG422". Archived from the original on 28 March 2014. Retrieved 31 January 2011. (Select Ephemeris Type:Elements and Center:@0)
- Kaib, Nathan A.; Becker, Andrew C.; Jones, R. Lynne; Puckett, Andrew W.; Bizyaev, Dmitry; Dilday, Benjamin; Frieman, Joshua A.; Oravetz, Daniel J.; Pan, Kaike; Quinn, Thomas; Schneider, Donald P.; Watters, Shannon (2009). "2006 SQ372: A Likely Long-Period Comet from the Inner Oort Cloud". The Astrophysical Journal. 695 (1): 268–275. arXiv:0901.1690. Bibcode:2009ApJ...695..268K. doi:10.1088/0004-637X/695/1/268. S2CID 16987581.



