| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
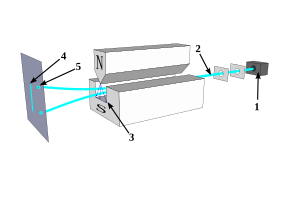
In quantum physics, the Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially-varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment were deflected, owing to the magnetic field gradient, from a straight path. The screen revealed discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.
After its conception by Otto Stern in 1921, the experiment was first successfully conducted with Walther Gerlach in early 1922.
Description
See also: Spin quantum numberThe Stern–Gerlach experiment involves sending silver atoms through an inhomogeneous magnetic field and observing their deflection. Silver atoms were evaporated using an electric furnace in a vacuum. Using thin slits, the atoms were guided into a flat beam and the beam sent through an inhomogeneous magnetic field before colliding with a metallic plate. The laws of classical physics predict that the collection of condensed silver atoms on the plate should form a thin solid line in the same shape as the original beam. However, the inhomogeneous magnetic field caused the beam to split in two separate directions, creating two lines on the metallic plate.
The results show that particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object, but that takes only certain quantized values. Another important result is that only one component of a particle's spin can be measured at one time, meaning that the measurement of the spin along the z-axis destroys information about a particle's spin along the x and y axis.
The experiment is normally conducted using electrically neutral particles such as silver atoms. This avoids the large deflection in the path of a charged particle moving through a magnetic field and allows spin-dependent effects to dominate.
If the particle is treated as a classical spinning magnetic dipole, it will precess in a magnetic field because of the torque that the magnetic field exerts on the dipole (see torque-induced precession). If it moves through a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the trajectory of the particle is unaffected. However, if the magnetic field is inhomogeneous then the force on one end of the dipole will be slightly greater than the opposing force on the other end, so that there is a net force which deflects the particle's trajectory. If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by an amount proportional to the dot product of its magnetic moment with the external field gradient, producing some density distribution on the detector screen. Instead, the particles passing through the Stern–Gerlach apparatus are deflected either up or down by a specific amount. This was a measurement of the quantum observable now known as spin angular momentum, which demonstrated possible outcomes of a measurement where the observable has a discrete set of values or point spectrum.
Although some discrete quantum phenomena, such as atomic spectra, were observed much earlier, the Stern–Gerlach experiment allowed scientists to directly observe separation between discrete quantum states for the first time.
Theoretically, quantum angular momentum of any kind has a discrete spectrum, which is sometimes briefly expressed as "angular momentum is quantized".
Experiment using particles with +1/2 or −1/2 spin
If the experiment is conducted using charged particles like electrons, there will be a Lorentz force that tends to bend the trajectory in a circle. This force can be cancelled by an electric field of appropriate magnitude oriented transverse to the charged particle's path.

Electrons are spin-1/2 particles. These have only two possible spin angular momentum values measured along any axis, or , a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). If one measures the spin along a vertical axis, electrons are described as "spin up" or "spin down", based on the magnetic moment pointing up or down, respectively.
To mathematically describe the experiment with spin particles, it is easiest to use Dirac's bra–ket notation. As the particles pass through the Stern–Gerlach device, they are deflected either up or down, and observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number , which can take on one of the two possible allowed values, either or . The act of observing (measuring) the momentum along the axis corresponds to the -axis angular momentum operator, often denoted . In mathematical terms, the initial state of the particles is
where constants and are complex numbers. This initial state spin can point in any direction. The squares of the absolute values and are respectively the probabilities for a system in the state to be found in and after the measurement along axis is made. The constants and must also be normalized in order that the probability of finding either one of the values be unity, that is we must ensure that . However, this information is not sufficient to determine the values of and , because they are complex numbers. Therefore, the measurement yields only the squared magnitudes of the constants, which are interpreted as probabilities.
Sequential experiments
If we link multiple Stern–Gerlach apparatuses (the rectangles containing S-G), we can clearly see that they do not act as simple selectors, i.e. filtering out particles with one of the states (pre-existing to the measurement) and blocking the others. Instead they alter the state by observing it (as in light polarization). In the figure below, x and z name the directions of the (inhomogenous) magnetic field, with the x-z-plane being orthogonal to the particle beam. In the three S-G systems shown below, the cross-hatched squares denote the blocking of a given output, i.e. each of the S-G systems with a blocker allows only particles with one of two states to enter the next S-G apparatus in the sequence.


Experiment 1
The top illustration shows that when a second, identical, S-G apparatus is placed at the exit of the first apparatus, only z+ is seen in the output of the second apparatus. This result is expected since all particles at this point are expected to have z+ spin, as only the z+ beam from the first apparatus entered the second apparatus.

Experiment 2
The middle system shows what happens when a different S-G apparatus is placed at the exit of the z+ beam resulting of the first apparatus, the second apparatus measuring the deflection of the beams on the x axis instead of the z axis. The second apparatus produces x+ and x- outputs. Now classically we would expect to have one beam with the x characteristic oriented + and the z characteristic oriented +, and another with the x characteristic oriented - and the z characteristic oriented +.

Experiment 3
The bottom system contradicts that expectation. The output of the third apparatus which measures the deflection on the z axis again shows an output of z- as well as z+. Given that the input to the second S-G apparatus consisted only of z+, it can be inferred that a S-G apparatus must be altering the states of the particles that pass through it. This experiment can be interpreted to exhibit the uncertainty principle: since the angular momentum cannot be measured on two perpendicular directions at the same time, the measurement of the angular momentum on the x direction destroys the previous determination of the angular momentum in the z direction. That's why the third apparatus measures renewed z+ and z- beams like the x measurement really made a clean slate of the z+ output.
History

The Stern–Gerlach experiment was conceived by Otto Stern in 1921 and performed by him and Walther Gerlach in Frankfurt in 1922. At the time of the experiment, the most prevalent model for describing the atom was the Bohr-Sommerfeld model, which described electrons as going around the positively charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. The Stern–Gerlach experiment was meant to test the Bohr–Sommerfeld hypothesis that the direction of the angular momentum of a silver atom is quantized.
The experiment was first performed with an electromagnet that allowed the non-uniform magnetic field to be turned on gradually from a null value. When the field was null, the silver atoms were deposited as a single band on the detecting glass slide. When the field was made stronger, the middle of the band began to widen and eventually to split into two, so that the glass-slide image looked like a lip-print, with an opening in the middle, and closure at either end. In the middle, where the magnetic field was strong enough to split the beam into two, statistically half of the silver atoms had been deflected by the non-uniformity of the field.
Note that the experiment was performed several years before George Uhlenbeck and Samuel Goudsmit formulated their hypothesis about the existence of electron spin in 1925. Even though the result of the Stern−Gerlach experiment has later turned out to be in agreement with the predictions of quantum mechanics for a spin-1/2 particle, the experimental result was also consistent with the Bohr–Sommerfeld theory.
In 1927, T.E. Phipps and J.B. Taylor reproduced the effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms. However, in 1926 the non-relativistic scalar Schrödinger equation had incorrectly predicted the magnetic moment of hydrogen to be zero in its ground state. To correct this problem Wolfgang Pauli considered a spin-1/2 version of the Schrödinger equation using the 3 Pauli matrices which now bear his name, which was later shown by Paul Dirac in 1928 to be a consequence of his relativistic Dirac equation.
In the early 1930s Stern, together with Otto Robert Frisch and Immanuel Estermann improved the molecular beam apparatus sufficiently to measure the magnetic moment of the proton, a value nearly 2000 times smaller than the electron moment. In 1931, theoretical analysis by Gregory Breit and Isidor Isaac Rabi showed that this apparatus could be used to measure nuclear spin whenever the electronic configuration of the atom was known. The concept was applied by Rabi and Victor W. Cohen in 1934 to determine the spin of sodium atoms.
In 1938 Rabi and coworkers inserted an oscillating magnetic field element into their apparatus, inventing nuclear magnetic resonance spectroscopy. By tuning the frequency of the oscillator to the frequency of the nuclear precessions they could selectively tune into each quantum level of the material under study. Rabi was awarded the Nobel Prize in 1944 for this work.
Importance
The Stern–Gerlach experiment was the first direct evidence of angular-momentum quantization in quantum mechanics, and it strongly influenced later developments in modern physics:
- In the decade that followed, scientists showed using similar techniques, that the nuclei of some atoms also have quantized angular momentum. It is the interaction of this nuclear angular momentum with the spin of the electron that is responsible for the hyperfine structure of the spectroscopic lines.
- Norman F. Ramsey later modified the Rabi apparatus to improve its sensitivity (using the separated oscillatory field method). In the early sixties, Ramsey, H. Mark Goldenberg, and Daniel Kleppner used a Stern–Gerlach system to produce a beam of polarized hydrogen as the source of energy for the hydrogen maser. This led to developing an extremely stable clock based on a hydrogen maser. From 1967 until 2019, the second was defined based on 9,192,631,770 Hz hyperfine transition of a cesium-133 atom; the atomic clock which is used to set this standard is an application of Ramsey's work.
- The Stern–Gerlach experiment has become a prototype for quantum measurement, demonstrating the observation of a discrete value (eigenvalue) of a physical property, previously assumed to be continuous. Entering the Stern–Gerlach magnet, the direction of the silver atom's magnetic moment is indefinite, but when the atom is registered at the screen, it is observed to be at either one spot or the other, and this outcome cannot be predicted in advance. Because the experiment illustrates the character of quantum measurements, The Feynman Lectures on Physics use idealized Stern–Gerlach apparatuses to explain the basic mathematics of quantum theory.
See also
References
- ^ Gerlach, W.; Stern, O. (1922). "Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld" [The experimental proof of directional quantization in the magnetic field]. Zeitschrift für Physik. 9 (1): 349–352. Bibcode:1922ZPhy....9..349G. doi:10.1007/BF01326983. S2CID 186228677.
- Franklin, Allan; Perovic, Slobodan. "Experiment in Physics, Appendix 5". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2016 ed.). Retrieved 2018-08-14.
- Friedrich, B.; Herschbach, D. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today. 56 (12): 53. Bibcode:2003PhT....56l..53F. doi:10.1063/1.1650229. S2CID 17572089.
- Castelvecchi, D. (2022). "The Stern–Gerlach experiment at 100". Nature Reviews Physics. 4 (3): 140–142. Bibcode:2022NatRP...4..140C. doi:10.1038/s42254-022-00436-4. S2CID 247184330.
- Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms" [The magnetic moment of the silver atom]. Zeitschrift für Physik. 9 (1): 353–355. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984. S2CID 126109346.
- Gerlach, W.; Stern, O. (1922). "Der experimentelle Nachweis des magnetischen Moments des Silberatoms" [The experimental proof of the magnetic moment of the silver atom]. Zeitschrift für Physik. 8 (1): 110–111. Bibcode:1922ZPhy....8..110G. doi:10.1007/BF01329580. S2CID 122648402.
- Mott, N.F., Massey, H.S.W. (1965/1971). The Theory of Atomic Collisions, third edition, Oxford University Press, Oxford UK, pp. 214–219, §2, Ch. IX, reprinted in Wheeler, J.A.; Zurek, W.H. (1983). Quantum Theory and Measurement. Princeton NJ: Princeton University Press. pp. 701–706.
- Rutherford, George H.; Grobe, Rainer (1997). "Comment on "Stern-Gerlach Effect for Electron Beams"". Phys. Rev. Lett. 81 (4772): 4772. Bibcode:1998PhRvL..81.4772R. doi:10.1103/PhysRevLett.81.4772.
- Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. pp. 14–18. ISBN 0-7923-2549-4.
- ^ Sakurai, J.-J. (1985). Modern Quantum Mechanics. Addison-Wesley. ISBN 0-201-53929-2.
- ^ Qinxun, Li (June 8, 2020). "Stern Gerlach Experiment:Descriptions and Developments". University of Science and Technology of China: 2–5. Retrieved 24 November 2020.
- Castelvecchi, Davide (2020). "Just a moment". Nature Physics. 16 (9): 994. Bibcode:2020NatPh..16..994C. doi:10.1038/s41567-020-1022-6. S2CID 225215678.
- Kragh, Helge (2012). "The Bohr–Sommerfeld theory". Niels Bohr and the quantum atom: The Bohr model of atomic structure 1913–1925. Oxford University Press. pp. 140–181. doi:10.1093/acprof:oso/9780199654987.003.0004. ISBN 978-0-19-965498-7.
- Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld" [A way to experimentally test directional quantization in a magnetic field]. Zeitschrift für Physik. 7 (1): 249–253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793. S2CID 186234469.
- French, A.P., Taylor, E.F. (1979). An Introduction to Quantum Physics, Van Nostrand Reinhold, London, ISBN 0-442-30770-5, pp. 428–442.
- Eisberg, Robert; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). Wiley. p. 277. ISBN 9780471873730.
- Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics. 26B (1): 75–86. Bibcode:1995SHPMP..26...75W. doi:10.1016/1355-2198(95)00002-B.
- Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review. 29 (2): 309–320. Bibcode:1927PhRv...29..309P. doi:10.1103/PhysRev.29.309.
- Kellogg, J. B. M.; Millman, S. (1946-07-01). "The Molecular Beam Magnetic Resonance Method. The Radiofrequency Spectra of Atoms and Molecules". Reviews of Modern Physics. 18 (3): 323–352. doi:10.1103/RevModPhys.18.323. ISSN 0034-6861.
- ^ Rabi, I.I.; Zacharias, J.R.; Millman, S. & Kusch, P. (1938). "A New Method of Measuring Nuclear Magnetic Moment". Physical Review. 53 (4): 318–327. Bibcode:1938PhRv...53..318R. doi:10.1103/PhysRev.53.318.
- Hamilton, Donald R. (1941-12-01). "Molecular Beams and Nuclear Moments". American Journal of Physics. 9 (6): 319–337. doi:10.1119/1.1991712. ISSN 0002-9505.
- "The Nobel Prize in Physics 1944". NobelPrize.org.
- Johnston, Hamish (2022-12-01). "100 years of the Stern–Gerlach experiment". Physics World. 35 (12): 27–30. doi:10.1088/2058-7058/35/12/30. ISSN 0953-8585.
- Griffiths, David (2005). Introduction to Quantum Mechanics (2nd ed.). Pearson Prentice Hall. p. 267. ISBN 0-13-111892-7.
- "Norman F. Ramsey – Autobiography". The Nobel Foundation. Retrieved June 13, 2013.
- Ramsey, Norman F. (1968). "The Atomic Hydrogen Maser". American Scientist. 56 (4): 420–438. ISSN 0003-0996. JSTOR 27828332.
- "Nobel Prize press release". The Nobel Foundation. Retrieved June 13, 2013.
- Bohm, David (1951). Quantum Theory. New York: Prentice-Hall. pp. 326–330.
- Gottfried, Kurt (1966). Quantum Mechanics. New York: W. A. Benjamin, Inc. pp. 170–174.
- Eisberg, Robert (1961). Fundamentals of Modern Physics. New York: John Wiley & Sons. pp. 334–338. ISBN 0-471-23463-X.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew L. (2006) . "5. Spin One". The Feynman Lectures on Physics. Vol. 3 (Definitive ed.). San Francisco, Calif.: Pearson Addison Wesley. ISBN 978-0-8053-9045-2.
- Gale, W.; Guth, E.; Trammell, G. T. (1968-01-25). "Determination of the Quantum State by Measurements". Physical Review. 165 (5): 1434–1436. doi:10.1103/PhysRev.165.1434.
- Ududec, Cozmin; Barnum, Howard; Emerson, Joseph (March 2011). "Three Slit Experiments and the Structure of Quantum Theory". Foundations of Physics. 41 (3): 396–405. arXiv:0909.4787. Bibcode:2011FoPh...41..396U. doi:10.1007/s10701-010-9429-z.
Further reading
- Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). "Stern-Gerlach dynamics with quantum propagators". Physical Review A. 83 (1): 012109–1–12. Bibcode:2011PhRvA..83a2109H. doi:10.1103/PhysRevA.83.012109.
- Margalit, Yair; Zhou, Zhifan; Machluf, Shimon; Japha, Yonathan; Moukouri, Samuel; Folman, Ron (2019-07-23). "Analysis of a high-stability Stern–Gerlach spatial fringe interferometer". New Journal of Physics. 21 (7): 073040. Bibcode:2019NJPh...21g3040M. doi:10.1088/1367-2630/ab2fdc.
- Reinisch, G. (1999). "Stern–Gerlach experiment as the pioneer—and probably the simplest—quantum entanglement test?". Physics Letters A. 259 (6): 427–430. Bibcode:1999PhLA..259..427R. doi:10.1016/S0375-9601(99)00472-7.
- Savitsky, Zack (2023-12-05). "The (Often) Overlooked Experiment That Revealed the Quantum World". Quanta Magazine.
- Venugopalan, A. (1997). "Decoherence and Schrödinger-cat states in a Stern−Gerlach-type experiment". Physical Review A. 56 (5): 4307–4310. Bibcode:1997PhRvA..56.4307V. doi:10.1103/PhysRevA.56.4307.
- Zwiebach, Barton (2022). "12.2: The Stern–Gerlach experiment". Mastering Quantum Mechanics: Essentials, Theory, and Applications. MIT Press. ISBN 978-0-262-04613-8.
External links
- Stern–Gerlach Experiment Java Applet Animation
- Stern–Gerlach Experiment Flash Model
- Detailed explanation of the Stern–Gerlach Experiment
- Animation, applications and research linked to the spin (Université Paris Sud)
- Wave Mechanics and Stern–Gerlach experiment at MIT OpenCourseWare

 or
or  , a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). If one measures the spin along a vertical axis, electrons are described as "spin up" or "spin down", based on the magnetic moment pointing up or down, respectively.
, a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). If one measures the spin along a vertical axis, electrons are described as "spin up" or "spin down", based on the magnetic moment pointing up or down, respectively.
 particles, it is easiest to use
particles, it is easiest to use  , which can take on one of the two possible allowed values, either
, which can take on one of the two possible allowed values, either  axis corresponds to the
axis corresponds to the  . In mathematical terms, the initial state of the particles is
. In mathematical terms, the initial state of the particles is

 and
and  are complex numbers. This initial state spin can point in any direction. The squares of the
are complex numbers. This initial state spin can point in any direction. The squares of the  and
and  are respectively the probabilities for a system in the state
are respectively the probabilities for a system in the state  to be found in
to be found in  and
and  after the measurement along
after the measurement along  . However, this information is not sufficient to determine the values of
. However, this information is not sufficient to determine the values of  spin of
spin of