| Name | Year | Flights | Location |
|---|---|---|---|
| Mercury-Redstone 3 Mercury-Redstone 4 |
1961 | 2 | Cape Canaveral |
| X-15 Flight 90 X-15 Flight 91 |
1963 | 2 | Edwards AFB |
| Soyuz 18a | 1975 | 1 | Baikonur Cosmodrome |
| SpaceShipOne Flight 15P SpaceShipOne Flight 16P SpaceShipOne Flight 17P |
2004 | 3 | Mojave Air and Space Port |
| Blue Origin NS-16 Blue Origin NS-18 Blue Origin NS-19 |
2021 | 3 | Corn Ranch |
| Blue Origin NS-20 Blue Origin NS-21 |
2022 | 3 | |
| Blue Origin NS-25 Blue Origin NS-26 |
2024 | 2 |
| Name | Year | Flights | Location |
|---|---|---|---|
| X-15 Flight 62 | 1962 | 1 | Edwards AFB |
| X-15 Flight 77 X-15 Flight 87 |
1963 | 2 | |
| X-15 Flight 138 X-15 Flight 143 X-15 Flight 150 X-15 Flight 153 |
1965 | 4 | |
| X-15 Flight 174 | 1966 | 1 | |
| X-15 Flight 190 X-15 Flight 191 |
1967 | 2 | |
| X-15 Flight 197 | 1968 | 1 | |
| Soyuz MS-10 | 2018 | 1 | Baikonur Cosmodrome |
| VSS Unity VP-03 | 2018 | 1 | Mojave Air and Space Port |
| VSS Unity VF-01 | 2019 | 1 | |
| VSS Unity Unity21 VSS Unity Unity22 |
2021 | 2 | Spaceport America |
| VSS Unity Unity25 Galactic 01 Galactic 02 Galactic 03 Galactic 04 Galactic 05 |
2023 | 6 | Spaceport America |
| Galactic 06 Galactic 07 |
2024 | 2 | Spaceport America |
A sub-orbital spaceflight is a spaceflight in which the spacecraft reaches outer space, but its trajectory intersects the surface of the gravitating body from which it was launched. Hence, it will not complete one orbital revolution, will not become an artificial satellite nor will it reach escape velocity.
For example, the path of an object launched from Earth that reaches the Kármán line (about 83 km – 100 km above sea level), and then falls back to Earth, is considered a sub-orbital spaceflight. Some sub-orbital flights have been undertaken to test spacecraft and launch vehicles later intended for orbital spaceflight. Other vehicles are specifically designed only for sub-orbital flight; examples include crewed vehicles, such as the X-15 and SpaceShipTwo, and uncrewed ones, such as ICBMs and sounding rockets.
Flights which attain sufficient velocity to go into low Earth orbit, and then de-orbit before completing their first full orbit, are not considered sub-orbital. Examples of this include flights of the Fractional Orbital Bombardment System.
A flight that does not reach space is still sometimes called sub-orbital, but cannot officially be classified as a "sub-orbital spaceflight". Usually a rocket is used, but some experimental sub-orbital spaceflights have also been achieved via the use of space guns.
Altitude requirement
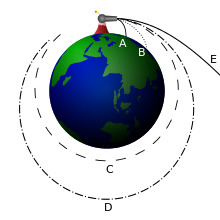
By definition, a sub-orbital spaceflight reaches an altitude higher than 100 km (62 mi) above sea level. This altitude, known as the Kármán line, was chosen by the Fédération Aéronautique Internationale because it is roughly the point where a vehicle flying fast enough to support itself with aerodynamic lift from the Earth's atmosphere would be flying faster than orbital speed. The US military and NASA award astronaut wings to those flying above 50 mi (80 km), although the U.S. State Department does not show a distinct boundary between atmospheric flight and spaceflight.
Orbit
During freefall the trajectory is part of an elliptic orbit as given by the orbit equation. The perigee distance is less than the radius of the Earth R including atmosphere, hence the ellipse intersects the Earth, and hence the spacecraft will fail to complete an orbit. The major axis is vertical, the semi-major axis a is more than R/2. The specific orbital energy is given by:
where is the standard gravitational parameter.
Almost always a < R, corresponding to a lower than the minimum for a full orbit, which is
Thus the net extra specific energy needed compared to just raising the spacecraft into space is between 0 and .
Speed, range, and altitude
To minimize the required delta-v (an astrodynamical measure which strongly determines the required fuel), the high-altitude part of the flight is made with the rockets off (this is technically called free-fall even for the upward part of the trajectory). (Compare with Oberth effect.) The maximum speed in a flight is attained at the lowest altitude of this free-fall trajectory, both at the start and at the end of it.
If one's goal is simply to "reach space", for example in competing for the Ansari X Prize, horizontal motion is not needed. In this case the lowest required delta-v, to reach 100 km altitude, is about 1.4 km/s. Moving slower, with less free-fall, would require more delta-v.
Compare this with orbital spaceflights: a low Earth orbit (LEO), with an altitude of about 300 km, needs a speed around 7.7 km/s, requiring a delta-v of about 9.2 km/s. (If there were no atmospheric drag the theoretical minimum delta-v would be 8.1 km/s to put a craft into a 300-kilometer high orbit starting from a stationary point like the South Pole. The theoretical minimum can be up to 0.46 km/s less if launching eastward from near the equator.)
For sub-orbital spaceflights covering a horizontal distance the maximum speed and required delta-v are in between those of a vertical flight and a LEO. The maximum speed at the lower ends of the trajectory are now composed of a horizontal and a vertical component. The higher the horizontal distance covered, the greater the horizontal speed will be. (The vertical velocity will increase with distance for short distances but will decrease with distance at longer distances.) For the V-2 rocket, just reaching space but with a range of about 330 km, the maximum speed was 1.6 km/s. Scaled Composites SpaceShipTwo which is under development will have a similar free-fall orbit but the announced maximum speed is 1.1 km/s (perhaps because of engine shut-off at a higher altitude).
For larger ranges, due to the elliptic orbit the maximum altitude can be much more than for a LEO. On a 10,000-kilometer intercontinental flight, such as that of an intercontinental ballistic missile or possible future commercial spaceflight, the maximum speed is about 7 km/s, and the maximum altitude may be more than 1300 km. Any spaceflight that returns to the surface, including sub-orbital ones, will undergo atmospheric reentry. The speed at the start of the reentry is basically the maximum speed of the flight. The aerodynamic heating caused will vary accordingly: it is much less for a flight with a maximum speed of only 1 km/s than for one with a maximum speed of 7 or 8 km/s.
The minimum delta-v and the corresponding maximum altitude for a given range can be calculated, d, assuming a spherical Earth of circumference 40000 km and neglecting the Earth's rotation and atmosphere. Let θ be half the angle that the projectile is to go around the Earth, so in degrees it is 45°×d/10000 km. The minimum-delta-v trajectory corresponds to an ellipse with one focus at the centre of the Earth and the other at the point halfway between the launch point and the destination point (somewhere inside the Earth). (This is the orbit that minimizes the semi-major axis, which is equal to the sum of the distances from a point on the orbit to the two foci. Minimizing the semi-major axis minimizes the specific orbital energy and thus the delta-v, which is the speed of launch.) Geometrical arguments lead then to the following (with R being the radius of the Earth, about 6370 km):
The altitude of apogee is maximized (at about 1320 km) for a trajectory going one quarter of the way around the Earth (10000 km). Longer ranges will have lower apogees in the minimal-delta-v solution.
(where g is the acceleration of gravity at the Earth's surface). The Δv increases with range, leveling off at 7.9 km/s as the range approaches 20000 km (halfway around the world). The minimum-delta-v trajectory for going halfway around the world corresponds to a circular orbit just above the surface (of course in reality it would have to be above the atmosphere). See lower for the time of flight.
An intercontinental ballistic missile is defined as a missile that can hit a target at least 5500 km away, and according to the above formula this requires an initial speed of 6.1 km/s. Increasing the speed to 7.9 km/s to attain any point on Earth requires a considerably larger missile because the amount of fuel needed goes up exponentially with delta-v (see Rocket equation).
The initial direction of a minimum-delta-v trajectory points halfway between straight up and straight toward the destination point (which is below the horizon). Again, this is the case if the Earth's rotation is ignored. It is not exactly true for a rotating planet unless the launch takes place at a pole.
Flight duration
In a vertical flight of not too high altitudes, the time of the free-fall is both for the upward and for the downward part the maximum speed divided by the acceleration of gravity, so with a maximum speed of 1 km/s together 3 minutes and 20 seconds. The duration of the flight phases before and after the free-fall can vary.
For an intercontinental flight the boost phase takes 3 to 5 minutes, the free-fall (midcourse phase) about 25 minutes. For an ICBM the atmospheric reentry phase takes about 2 minutes; this will be longer for any soft landing, such as for a possible future commercial flight. Test flight 4 of the SpaceX 'Starship' performed such a flight with a lift off from Texas and a simulated soft touchdown in the Indian Ocean 66 minutes after liftoff.
Sub-orbital flights can last from just seconds to days. Pioneer 1 was NASA's first space probe, intended to reach the Moon. A partial failure caused it to instead follow a sub-orbital trajectory, reentering the Earth's atmosphere 43 hours after launch.
To calculate the time of flight for a minimum-delta-v trajectory, according to Kepler's third law, the period for the entire orbit (if it did not go through the Earth) would be:
Using Kepler's second law, we multiply this by the portion of the area of the ellipse swept by the line from the centre of the Earth to the projectile:
This gives about 32 minutes for going a quarter of the way around the Earth, and 42 minutes for going halfway around. For short distances, this expression is asymptotic to .
From the form involving arccosine, the derivative of the time of flight with respect to d (or θ) goes to zero as d approaches 20000 km (halfway around the world). The derivative of Δv also goes to zero here. So if d = 19000 km, the length of the minimum-delta-v trajectory will be about 19500 km, but it will take only a few seconds less time than the trajectory for d = 20000 km (for which the trajectory is 20000 km long).
Flight profiles


While there are a great many possible sub-orbital flight profiles, it is expected that some will be more common than others.

Ballistic missiles
The first sub-orbital vehicles which reached space were ballistic missiles. The first ballistic missile to reach space was the German V-2, the work of the scientists at Peenemünde, on October 3, 1942, which reached an altitude of 53 miles (85 km). Then in the late 1940s the US and USSR concurrently developed missiles all of which were based on the V-2 Rocket, and then much longer range Intercontinental Ballistic Missiles (ICBMs). There are now many countries who possess ICBMs and even more with shorter range Intermediate Range Ballistic Missiles (IRBMs).
Tourist flights
Sub-orbital tourist flights will initially focus on attaining the altitude required to qualify as reaching space. The flight path will be either vertical or very steep, with the spacecraft landing back at its take-off site.
The spacecraft will shut off its engines well before reaching maximum altitude, and then coast up to its highest point. During a few minutes, from the point when the engines are shut off to the point where the atmosphere begins to slow down the downward acceleration, the passengers will experience weightlessness.
Megaroc had been planned for sub-orbital spaceflight by the British Interplanetary Society in the 1940s.
In late 1945, a group led by M. Tikhonravov K. and N. G. Chernysheva at the Soviet NII-4 academy (dedicated to rocket artillery science and technology), began work on a stratospheric rocket project, VR-190, aimed at vertical flight by a crew of two pilots, to an altitude of 200 km (65,000 ft) using captured V-2.
In 2004, a number of companies worked on vehicles in this class as entrants to the Ansari X Prize competition. The Scaled Composites SpaceShipOne was officially declared by Rick Searfoss to have won the competition on October 4, 2004, after completing two flights within a two-week period.
In 2005, Sir Richard Branson of the Virgin Group announced the creation of Virgin Galactic and his plans for a 9-seat capacity SpaceShipTwo named VSS Enterprise. It has since been completed with eight seats (one pilot, one co-pilot and six passengers) and has taken part in captive-carry tests and with the first mother-ship WhiteKnightTwo, or VMS Eve. It has also completed solitary glides, with the movable tail sections in both fixed and "feathered" configurations. The hybrid rocket motor has been fired multiple times in ground-based test stands, and was fired in a powered flight for the second time on 5 September 2013. Four additional SpaceShipTwos have been ordered and will operate from the new Spaceport America. Commercial flights carrying passengers were expected in 2014, but became cancelled due to the disaster during SS2 PF04 flight. Branson stated, "e are going to learn from what went wrong, discover how we can improve safety and performance and then move forwards together."
Scientific experiments
A major use of sub-orbital vehicles today is as scientific sounding rockets. Scientific sub-orbital flights began in the 1920s when Robert H. Goddard launched the first liquid fueled rockets, however they did not reach space altitude. In the late 1940s, captured German V-2 ballistic missiles were converted into V-2 sounding rockets which helped lay the foundation for modern sounding rockets. Today there are dozens of different sounding rockets on the market, from a variety of suppliers in various countries. Typically, researchers wish to conduct experiments in microgravity or above the atmosphere.
Sub-orbital transportation
Research, such as that done for the X-20 Dyna-Soar project suggests that a semi-ballistic sub-orbital flight could travel from Europe to North America in less than an hour.
However, the size of rocket, relative to the payload, necessary to achieve this, is similar to an ICBM. ICBMs have delta-v's somewhat less than orbital; and therefore would be somewhat cheaper than the costs for reaching orbit, but the difference is not large.
Due to the high cost of spaceflight, suborbital flights are likely to be initially limited to high value, very high urgency cargo deliveries such as courier flights, military fast-response operations or space tourism.
The SpaceLiner is a hypersonic suborbital spaceplane concept that could transport 50 passengers from Australia to Europe in 90 minutes or 100 passengers from Europe to California in 60 minutes. The main challenge lies in increasing the reliability of the different components, particularly the engines, in order to make their use for passenger transportation on a daily basis possible.
SpaceX is potentially considering using their Starship as a sub-orbital point-to-point transportation system.
Notable uncrewed sub-orbital spaceflights
- The first sub-orbital space flight was on 20 June 1944, when MW 18014, a V-2 test rocket, launched from Peenemünde in Germany and reached 176 kilometres altitude.
- Bumper 5, a two-stage rocket launched from the White Sands Proving Grounds. On 24 February 1949 the upper stage reached an altitude of 248 miles (399 km) and a speed of 7,553 feet per second (2,302 m/s; Mach 6.8).
- Albert II, a male rhesus macaque, became the first mammal in space on 14 June 1949 in a sub-orbital flight from Holloman Air Force Base in New Mexico to an altitude of 83 miles (134 km) aboard a U.S. V-2 sounding rocket.
- USSR – Energia, 15 May 1987, a Polyus payload which failed to reach orbit
- SpaceX IFT-3, 14 March 2024, first successful Starship flight test, most massive object launched into a sub-orbital trajectory to date.
Crewed sub-orbital spaceflights
Above 100 km (62.14 mi) in altitude.
| Date (GMT) | Mission | Crew | Country | Remarks | |
|---|---|---|---|---|---|
| 1 | 1961-05-05 | Mercury-Redstone 3 | Alan Shepard | First crewed sub-orbital spaceflight, first American in space | |
| 2 | 1961-07-21 | Mercury-Redstone 4 | Virgil Grissom | Second crewed sub-orbital spaceflight, second American in space | |
| 3 | 1963-07-19 | X-15 Flight 90 | Joseph A. Walker | First winged craft in space | |
| 4 | 1963-08-22 | X-15 Flight 91 | Joseph A. Walker | First person and spacecraft to make two flights into space | |
| 5 | 1975-04-05 | Soyuz 18a | Vasili Lazarev Oleg Makarov |
Failed orbital launch. Aborted after malfunction during stage separation | |
| 6 | 2004-06-21 | SpaceShipOne flight 15P | Mike Melvill | First commercial spaceflight | |
| 7 | 2004-09-29 | SpaceShipOne flight 16P | Mike Melvill | First of two flights to win Ansari X-Prize | |
| 8 | 2004-10-04 | SpaceShipOne flight 17P | Brian Binnie | Second X-Prize flight, clinching award | |
| 9 | 2021-07-20 | Blue Origin NS-16 | Jeff Bezos Mark Bezos Wally Funk Oliver Daemen |
First crewed Blue Origin flight | |
| 10 | 2021-10-13 | Blue Origin NS-18 | Audrey Powers Chris Boshuizen Glen de Vries William Shatner |
Second crewed Blue Origin flight | |
| 11 | 2021-12-11 | Blue Origin NS-19 | Laura Shepard Churchley Michael Strahan Dylan Taylor Evan Dick Lane Bess Cameron Bess |
Third crewed Blue Origin flight | |
| 12 | 2022-03-31 | Blue Origin NS-20 | Marty Allen Sharon Hagle Marc Hagle Jim Kitchen George Nield Gary Lai |
Fourth crewed Blue Origin flight | |
| 13 | 2022-06-04 | Blue Origin NS-21 | Evan Dick Katya Echazarreta Hamish Harding Victor Correa Hespanha Jaison Robinson Victor Vescovo |
Fifth crewed Blue Origin flight | |
| 14 | 2022-08-04 | Blue Origin NS-22 | Coby Cotton Mário Ferreira Vanessa O'Brien Clint Kelly III Sara Sabry Steve Young |
Sixth crewed Blue Origin flight | |
| 15 | 2024-05-19 | Blue Origin NS-25 | Mason Angel Sylvain Chiron Ed Dwight Kenneth Hess Carol Schaller Gopichand Thotakura |
Seventh crewed Blue Origin flight | |
| 16 | 2024-08-29 | Blue Origin NS-26 | Nicolina Elrick Rob Ferl Eugene Grin Eiman Jahangir Karsen Kitchen Ephraim Rabin |
Eighth crewed Blue Origin flight | |
| 17 | 2024-11-22 | Blue Origin NS-28 | Henry (Hank) Wolfond Austin Litteral James (J.D.) Russell Sharon Hagle Marc Hagle Emily Calandrelli |
Ninth crewed Blue Origin flight |

Future of crewed sub-orbital spaceflight
Private companies such as Virgin Galactic, Armadillo Aerospace (reinvented as Exos Aerospace), Airbus, Blue Origin and Masten Space Systems are taking an interest in sub-orbital spaceflight, due in part to ventures like the Ansari X Prize. NASA and others are experimenting with scramjet-based hypersonic aircraft which may well be used with flight profiles that qualify as sub-orbital spaceflight. Non-profit entities like ARCASPACE and Copenhagen Suborbitals also attempt rocket-based launches.
Suborbital spaceflight projects
- Canadian Arrow
- CORONA
- DH-1 (rocket)
- Interorbital Systems
- Lunar Lander Challenge
- McDonnell Douglas DC-X
- Project Morpheus NASA program to continue developing ALHAT and Q landers
- Quad (rocket)
- Reusable Vehicle Testing program by JAXA
- Rocketplane XP
- SpaceX reusable launch system development program
- XCOR Lynx
See also
- Levels of spaceflight: Suborbital, orbital, interplanetary, interstellar and intergalatic
References
- Foust, Jeff (20 July 2021). "Blue Origin launches Bezos on first crewed New Shepard flight". SpaceNews. Retrieved 20 Jul 2021.
- Reinhardt, Dean N. (2007). "The Vertical Limit of State Sovereignty". Journal of Air Law and Commerce. 72 (1).
- "Martlet". Archived from the original on 2010-09-26.
- "100 km Altitude Boundary for Astronautics". Fédération Aéronautique Internationale. Archived from the original on 2011-08-09. Retrieved 2017-09-14.
- Whelan, Mary (5 June 2013). "X-15 Space Pioneers Now Honored as Astronauts". nasa.gov. Archived from the original on 11 June 2017. Retrieved 4 May 2018.
- "85. U.S. Statement, Definition and Delimitation of Outer Space And The Character And Utilization Of The Geostationary Orbit, Legal Subcommittee of the United Nations Committee on the Peaceful Uses of Outer Space at its 40th Session in Vienna from April". state.gov. Retrieved 4 May 2018.
- Blanco, Philip (September 2020). "Modeling ICBM Trajectories Around a Rotating Globe with Systems Tool Kit". The Physics Teacher. 58 (7): 494–496. Bibcode:2020PhTea..58..494B. doi:10.1119/10.0002070. S2CID 225017449.
- "Pioneer 1 - NSSDC ID: 1958-007A". NASA NSSDC.
- Germany's V-2 Rocket, Kennedy, Gregory P.
- Hollingham, Richard. "How a Nazi rocket could have put a Briton in space". bbc.com. Archived from the original on 14 November 2016. Retrieved 4 May 2018.
- "Megaroc". www.bis-space.com. Archived from the original on 30 October 2016. Retrieved 4 May 2018.
- Anatoli I. Kiselev; Alexander A. Medvedev; Valery A. Menshikov (December 2012). Astronautics: Summary and Prospects. Translated by V. Sherbakov; N. Novichkov; A. Nechaev. Springer Science & Business Media. pp. 1–2. ISBN 9783709106488.
- "Scaled Composites: Projects - Test Logs for SpaceShipTwo". Archived from the original on 2013-08-16. Retrieved 2013-08-14.
- "Branson on Virgin Galactic crash: 'Space is hard – but worth it'". CNET. Retrieved August 1, 2015.
- "ch2". history.nasa.gov. Archived from the original on 2015-11-29. Retrieved 2015-11-28.
- "The Space Review: Point-to-point suborbital transportation: sounds good on paper, but..." www.thespacereview.com. Archived from the original on 1 August 2017. Retrieved 4 May 2018.
- Sippel, M. (2010). "Promising roadmap alternatives for the SpaceLiner" (PDF). Acta Astronautica. 66 (11–12): 1652–1658. Bibcode:2010AcAau..66.1652S. doi:10.1016/j.actaastro.2010.01.020.
- Ralph, Eric (30 May 2019). "SpaceX CEO Elon Musk wants to use Starships as Earth-to-Earth transports". Teslarati. Retrieved 31 May 2019.
- Walter Dornberger, Moewig, Berlin 1984. ISBN 3-8118-4341-9.
- "Bumper Project". White Sands Missile Range. Archived from the original on 2008-01-10.
- Amos, Jonathan (3 June 2014). "Airbus drops model 'space jet'". BBC News. Archived from the original on 4 May 2018. Retrieved 4 May 2018.
| Spaceflight | |||||||
|---|---|---|---|---|---|---|---|
| General | |||||||
| Applications | |||||||
| Human spaceflight |
| ||||||
| Spacecraft | |||||||
| Destinations | |||||||
| Space launch | |||||||
| Ground segment | |||||||
 is given by:
is given by:

 is the
is the 
 .
.









 .
.