In linguistics and philosophy, a vague predicate is one which gives rise to borderline cases. For example, the English adjective "tall" is vague since it is not clearly true or false for someone of middling height. By contrast, the word "prime" is not vague since every number is definitively either prime or not. Vagueness is commonly diagnosed by a predicate's ability to give rise to the Sorites paradox. Vagueness is separate from ambiguity, in which an expression has multiple denotations. For instance the word "bank" is ambiguous since it can refer either to a river bank or to a financial institution, but there are no borderline cases between both interpretations.
Vagueness is a major topic of research in philosophical logic, where it serves as a potential challenge to classical logic. Work in formal semantics has sought to provide a compositional semantics for vague expressions in natural language. Work in philosophy of language has addressed implications of vagueness for the theory of meaning, while metaphysicists have considered whether reality itself is vague.
Importance
The concept of vagueness has philosophical importance. Suppose one wants to come up with a definition of "right" in the moral sense. One wants a definition to cover actions that are clearly right and exclude actions that are clearly wrong, but what does one do with the borderline cases? Surely, there are such cases. Some philosophers say that one should try to come up with a definition that is itself unclear on just those cases. Others say that one has an interest in making his or her definitions more precise than ordinary language, or his or her ordinary concepts, themselves allow; they recommend one advances precising definitions.
In law
Vagueness is also a problem which arises in law, and in some cases, judges have to arbitrate regarding whether a borderline case does, or does not, satisfy a given vague concept. Examples include disability (how much loss of vision is required before one is legally blind?), human life (at what point from conception to birth is one a legal human being, protected for instance by laws against murder?), adulthood (most familiarly reflected in legal ages for driving, drinking, voting, consensual sex, etc.), race (how to classify someone of mixed racial heritage), etc. Even such apparently unambiguous concepts such as biological sex can be subject to vagueness problems, not just from transsexuals' gender transitions but also from certain genetic conditions which can give an individual mixed male and female biological traits (see intersex).
In science
Many scientific concepts are of necessity vague, for instance species in biology cannot be precisely defined, owing to unclear cases such as ring species. Nonetheless, the concept of species can be clearly applied in the vast majority of cases. As this example illustrates, to say that a definition is "vague" is not necessarily a criticism. Consider those animals in Alaska that are the result of breeding huskies and wolves: are they dogs? It is not clear: they are borderline cases of dogs. This means one's ordinary concept of doghood is not clear enough to let us rule conclusively in this case.
Approaches
The philosophical question of what the best theoretical treatment of vagueness is—which is closely related to the problem of the paradox of the heap, a.k.a. sorites paradox—has been the subject of much philosophical debate.
Fuzzy logic
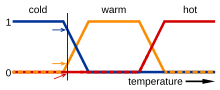
One theoretical approach is that of fuzzy logic, developed by American mathematician Lotfi Zadeh. Fuzzy logic proposes a gradual transition between "perfect falsity", for example, the statement "Bill Clinton is bald", to "perfect truth", for, say, "Patrick Stewart is bald". In ordinary logics, there are only two truth-values: "true" and "false". The fuzzy perspective differs by introducing an infinite number of truth-values along a spectrum between perfect truth and perfect falsity. Perfect truth may be represented by "1", and perfect falsity by "0". Borderline cases are thought of as having a "truth-value" anywhere between 0 and 1 (for example, 0.6). Advocates of the fuzzy logic approach have included K. F. Machina (1976) and Dorothy Edgington (1993).
Supervaluationism
Main article: SupervaluationismAnother theoretical approach is known as "supervaluationism". This approach has been defended by Kit Fine and Rosanna Keefe. Fine argues that borderline applications of vague predicates are neither true nor false, but rather are instances of "truth value gaps". He defends an interesting and sophisticated system of vague semantics, based on the notion that a vague predicate might be "made precise" in many alternative ways. This system has the consequence that borderline cases of vague terms yield statements that are neither true, nor false.
Given a supervaluationist semantics, one can define the predicate "supertrue" as meaning "true on all precisifications". This predicate will not change the semantics of atomic statements (e.g. "Frank is bald", where Frank is a borderline case of baldness), but does have consequences for logically complex statements. In particular, the tautologies of sentential logic, such as "Frank is bald or Frank is not bald", will turn out to be supertrue, since on any precisification of baldness, either "Frank is bald" or "Frank is not bald" will be true. Since the presence of borderline cases seems to threaten principles like this one (excluded middle), the fact that supervaluationism can "rescue" them is seen as a virtue.
Subvaluationism
See also: DialetheismSubvaluationism is the logical dual of supervaluationism, and has been defended by Dominic Hyde (2008) and Pablo Cobreros (2011). Whereas the supervaluationist characterises truth as 'supertruth', the subvaluationist characterises truth as 'subtruth', or "true on at least some precisifications".
Subvaluationism proposes that borderline applications of vague terms are both true and false. It thus has "truth-value gluts". According to this theory, a vague statement is true if it is true on at least one precisification and false if it is false under at least one precisification. If a vague statement comes out true under one precisification and false under another, it is both true and false. Subvaluationism ultimately amounts to the claim that vagueness is a truly contradictory phenomenon. Of a borderline case of "bald man" it would be both true and false to say that he is bald, and both true and false to say that he is not bald.
Epistemicist view
Main article: EpistemicismA fourth approach, known as "the epistemicist view", has been defended by Timothy Williamson (1994), R. A. Sorensen (1988) and (2001), and Nicholas Rescher (2009). They maintain that vague predicates do, in fact, draw sharp boundaries, but that one cannot know where these boundaries lie. One's confusion about whether some vague word does or does not apply in a borderline case is due to one's ignorance. For example, in the epistemicist view, there is a fact of the matter, for every person, about whether that person is old or not old; some people are ignorant of this fact.
As a property of objects
One possibility is that one's words and concepts are perfectly precise, but that objects themselves are vague. Consider Peter Unger's example of a cloud (from his famous 1980 paper, "The Problem of the Many"): it is not clear where the boundary of a cloud lies; for any given bit of water vapor, one can ask whether it is part of the cloud or not, and for many such bits, one will not know how to answer. So perhaps one's term 'cloud' denotes a vague object precisely. This strategy has been poorly received, in part due to Gareth Evans's short paper "Can There Be Vague Objects?" (1978). Evans's argument appears to show that there can be no vague identities (e.g. "Princeton = Princeton Borough"), but as Lewis (1988) makes clear, Evans takes for granted that there are in fact vague identities, and that any proof to the contrary cannot be right. Since the proof Evans produces relies on the assumption that terms precisely denote vague objects, the implication is that the assumption is false, and so the vague-objects view is wrong.
Still by, for instance, proposing alternative deduction rules involving Leibniz's law or other rules for validity some philosophers are willing to defend ontological vagueness as some kind of metaphysical phenomenon. One has, for example, Peter van Inwagen (1990), Trenton Merricks and Terence Parsons (2000).
Legal principle
In the common law system, vagueness is a possible legal defence against by-laws and other regulations. The legal principle is that delegated power cannot be used more broadly than the delegator intended. Therefore, a regulation may not be so vague as to regulate areas beyond what the law allows. Any such regulation would be "void for vagueness" and unenforceable. This principle is sometimes used to strike down municipal by-laws that forbid "explicit" or "objectionable" contents from being sold in a certain city; courts often find such expressions to be too vague, giving municipal inspectors discretion beyond what the law allows. In the US this is known as the vagueness doctrine and in Europe as the principle of legal certainty.
Essence and functioning
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. Find sources: "Vagueness" – news · newspapers · books · scholar · JSTOR (April 2023) (Learn how and when to remove this message) |
Vagueness is primarily a filter of natural human cognition, other tasks of vagueness are derived from that, and they are secondary. The ability to cognition is the basic natural equipment of human (and other creatures) allowing him to orient and survive in the real (material) world. The task of cognition is to obtain from the epistemologically incalculable (immensely vast and deep) reality to a human its cognitive (knowledge) model, containing an only finite amount of information. For this purpose, there must be a filter performing selection and thus reduction of information. It is the vagueness with which man perceive and then remember information about the real (material) world. Some information gained with less vagueness, others with greater one, according to the distance from the center (focus) of attention occupied by man during his act of cognition. Human is unable to acquire information other than vague one by his natural vague cognition. It is necessary to distinguish the internal cognitive model, i.e. the intrapsychic, stored and processed in human consciousness (and probably also in the unconscious), in hypothetical intrapsychic languages: imaginary, emotional and natural and in their mixture, and then the external model, represented in a suitable external language of communication.
Vagueness internal and external
Cognition and language (Law of maintaining accuracy of information): Communication language should have the same amount of vagueness, as have information gained by cognition (source of the information). That means, language must be tuned to appropriate cognition considering vagueness. This is one of secondary tasks of vagueness.
A person is able to speak about his inherently vague knowledge (contained in the intrapsychic cognitive model represented in hypothetical intrapsychic languages) in natural (generally informal language, e.g. Esperanto), of course only vaguely. The vagueness of knowledge caused by the filter of knowledge is primary, we call it internal vagueness (i.e. intrapsychic). The vagueness of a person's subsequent utterance is secondary vagueness. This utterance (transformation from intrapsychic languages to external communicative languages - it is called a formulation, see the semantic triangle) cannot reveal all the content of the personal intrapsychic cognitive model with all its inherent vagueness. The vagueness contained in the linguistic utterance (of external communication language) is called external vagueness.
Linguistically, only external vagueness can be grasped (modeled). We cannot model internal vagueness; it is part of the intrapsychic model, and this vagueness is contained in (vague, emotional, subjective and variable during time) interpretation of constructs (words, sentences) of informal language. This vagueness is hidden for the other human, he can only guess the amount of it. Informal languages, such as natural language, do not make it possible to distinguish between internal and external vagueness strictly, but only with a vague boundary.
Fortunately, however, informal languages use appropriate language constructs making meaning a little uncertain (e.g. indeterminate quantifiers POSSIBLY, SEVERAL, MAYBE, etc.). Such quantifiers allow natural language to use external vagueness more strongly and explicitly, thus allowing internal vagueness to be partially shifted up to external vagueness. It is a way to draw the addressee's attention to the vagueness of the message more explicitly and to quantify the vagueness, thus improving understanding in communication using natural language. But the main vagueness of informal languages is the internal vagueness, and the external vagueness serves only as an auxiliary tool.
Formal languages, mathematics, formal logic, programming languages (in principle, they must have zero internal vagueness of interpretation of all language constructs, i.e. they have exact interpretation) can model external vagueness by tools of vagueness and uncertainty representation: fuzzy sets and fuzzy logic, or by stochastic quantities and stochastic functions, as the exact sciences do. Principle is: If we admit more vagueness (uncertainty), we can gain more information during cognition. See e.g. possibilities of deterministic and stochastic physic. In other cases cognitive model of certain part of real world may be simplified, such a way, that certain amount of deterministic information is possible to replace by fuzzy or stochastic one.
Reducing internal vagueness
The internal vagueness of one person's message is hidden from another person, he can only guess that. We either have to accept internal vagueness, which is human, or we can try to reduce it, or completely eliminate it, which is scientific.
Demands on the accuracy of the formulation of scientific knowledge and its communication require minimizing the internal vagueness with which one connotes (vaguely, emotionally and subjectively interprets) linguistic constructs of the communication language, and thus improve the accuracy of the message. Various scientific procedures aim to improve the credibility and accuracy of the scientific knowledge obtained.
To formulate them, however, it is necessary to build a more precise language, with less (internal) vagueness of message than is common in daily life. This is done by purposefully (branch) constructed terminology allowing to more accurately describe the researched reality and the acquired knowledge about it. People properly educated in the field of terminology know it with little internal vagueness, so they know accurately what the individual terms mean. Basic concepts are always formed on the basis of consensus, the other derived from them by definition, to avoid to Circular definition. To improve the accuracy of research and communication (reducing the internal vagueness of connotation), tools such as classification schemes are used, such as the taxonomy of organisms by Carl von Linné.
This is how descriptive (non-exact) sciences do it. Thus, they use natural human cognition (with the Russell’s filter of vagueness) and refined natural language.
There is another continuation of the reduction of internal vagueness. The method of reducing internal vagueness to the extreme, that is zero, was realized by I. Newton. It is an epochal idea, and it needs to be explained how it can be realized.
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Vagueness" – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove this message) |
It follows from the above-mentioned Law of maintaining accuracy of information (optimization of the truthfulness of the message) saying, if we require to eliminate the internal vagueness in the knowledge completely (to zero) then of course it must first be completely eliminated in cognition (the source of information). This means that one (Newton) must avoid the intrusion of internal vagueness, that is, to choose some filter of cognition other than vagueness. Thus we pass from the natural human world to the artificial one. We call it the exact world and we will explain why.
In the case of natural language, it is not possible to completely remove (nullify) the internal vagueness, but it is possible to build artificial formal languages (mathematics, formal logics, programming languages) that have zero internal vagueness of connotation (so they have an exact interpretation) and cannot have another in principle. (Newton for this purpose has created formal language – theory of flux - theory of flowing – infinitesimal calculus). Languages with zero internal vagueness of their interpretation, i.e. the meaning of their linguistic constructions, have the property that all these constructions are understood by every appropriately educated person with absolutely precise, i.e. exact meaning. That is why they are part of the exact world. Thus, we have some language that is able to represent knowledge with zero internal vagueness. But these must first be acquired by adequate cognition, providing cognition also with zero internal vagueness, i.e. also from the exact world. And it is already evident that we are on the way to the creation of the scientific method that creates science belonging to the exact world, that is, an exact science is born.
It is still necessary to explain how to realize Newton`s exact cognition, that is, the cognition when the knowledge obtained from the real world is part of the exact world. The miraculous bridge between the real and exact worlds that makes this possible is called a quantity (e.g. electric field intensity, velocity, nitric acid concentration, etc.). It is common to both worlds, because in the exact world it is precisely delineated (every knowing person knows them with no doubts, so exactly), and in the real world it is an elemental measurable probe into that, and thus its elemental measurable representative. The quantity is the elementary building block of exact science. In exact sciences, it is always precisely defined, either consensually (basic set) or the other derived - International System of Units. And what about the artificial filter that allows Newton to avoid internal vagueness? For every problem of the real world that is to be grasped by Newton’s method of the exact science, it is necessary to choose a group of suitable quantities, find the natural laws that apply in the real world between them, and describe them in mathematical language. We get a mathematical knowledge (cognitive) model of a given part of the real world. A group of selected quantities forms a discrete Newtonian filter (sieve) through which man ‘’look’’ at a given part of the real world. Thus, in exact science, a given part of the real world is represented by a group of suitably chosen quantities and mathematically (programming language) described relations between them (more precisely between their names – symbols denoting them).
Exact science is a method that allows knowledge about the real world to be acquired and recorded so that it is part of the exact world. That is the method of modeling the real world by means of exact world, in other words, a method to mathematize the science.
Even exact science needs to have a tool, with which it can describe the uncertainty of the results (obtained – knowledge), whether out of necessity or the need to abandon excessive precision. Since that cannot (must not) be an internal vagueness, it can only use linguistically graspable uncertainty (external vagueness). For this purpose it has for its disposal a description of fuzzy or stochastic values of quantities, and fuzzy or stochastic relations (represented by mathematical functions) between quantities.
The difference between the non-exact sciences (called descriptive) and the exact sciences is that the former use natural human cognition (with the Russell’s filter of vagueness) and refined natural language, and the exact sciences use cognition based on the use of Newtonian discrete filter and thus the use of quantities, and artificial formal language. Artificial formal language also brings a powerful tool to exact science, which is formal inference (information formal processing) known from mathematics.
The above-mentioned tools of exact and non-exact science are general principles, and different branches of science use them in combination with both. They have their parts exact and inexact. Purely exact sciences, such as theoretical physics or mathematics, use natural language as meta-language.
Exact science provides most trustworthy knowledge. The question can certainly be raised as to whether all science can be transformed into an exact science. The answer is not. The condition for the establishment of an exact science is to find suitable quantities, and this is possible only for a small part of the real world and for specific views of it. In other words, the filter of vagueness makes it possible to vaguely know many; Newton's discrete filter makes it possible to know only little but exactly.
See also
- Essentially contested concept
- Fuzzy concept
- Imprecise language
- Obfuscation
- Relevance
- Unconstitutional vagueness
- Understanding
References
- Williamson, T. 1994. Vagueness, . London: Routledge.
The history of the problem of vagueness is traced, from the first Sorites Paradox to contemporary attempts to deal with higher-order vagueness such as many-valued logic, supervaluationism, and fuzzy logic. Technicalities are kept to a minimum to favour a clear account, extremely useful to both students and researchers. - Machina, K.F. 1976. "Truth, Belief and Vagueness", in Journal of Philosophical Logic Vol. 5. pp. 47-78.
- Edgington, D. (1997). Keefe, R.; Smith, P. (eds.). Vagueness by degrees (PDF). MIT Press. pp. 294–316.
- Kit Fine, The Limits of Abstraction (2002).
- Pablo Cobreros, (2011) "Paraconsistent Vagueness: A Positive Argument" Synthese 183(2): 211–227.
- Dominic Hyde and Mark Colyvan (2008) “Paraconsistent Vagueness: Why Not?” Australasian Journal of Logic 6: 107–121.
- Williamson, T. 1994. Vagueness London: Routledge.
- Sorensen, R.A. 1988. Blindspots. Oxford: Clarendon Press.
- Sorensen, Roy (2001). Vagueness and Contradiction. Oxford University Press.
- Rescher, N. 2009. Unknowability. Lexington Books.
Uses vagrant predicates to elucidate the problem. - Evans, G. (1978). "Can There Be Vague Objects?". Analysis. 38 (4): 208–. doi:10.1093/analys/38.4.208.
- Van Inwagen, Peter. 1990 Material Beings. Ithaca, NY: Cornell University Press.
- Parsons, Terence. 2000. Indeterminate Identity - Metaphysics and Semantics Oxford: Clarendon Press.
- ^ Russell, Bertrand (June 1923). "Vagueness". Australasian Journal of Psychology and Philosophy. 1 (2): 84–92. doi:10.1080/00048402308540623.
- Křemen, J.: Modely a systémy (Models and Systems), ACADEMIA, Publishing house of the Czech Academy of Sciences, Prague 2007, ISBN 978-80-200-1477-1
- ^ Osgood C. E, Suci G., Tannenbaum P.: The Measurement of Meaning. Urbana, Illinois, University of Illinois Press, 1957
- Bek R., Křemen J.: Logic, Cognitive Model and Reality, in: Proceedings of the 8th international symposium LOGICA ‘94, T.Childers, O. Majer ed., publ. by PHILOSOPHIA, The institute of Philosophy of the Academy of Sciences of Czech Republic, Prague 1995, pp. 193-199.
- Křemen, J. : Notes on Vagueness of Knowledge: Fuzzy Tools. In: Acta Polytechnica, Vol. 39, No 4/1999, pp. 81- 91. ISSN 1210-2709, Czech Technical University in Prague
- Russell B.: Vagueness. In: The Australasian Journal of Psychology and Philosophy 1, June 1923, pp. 84--92.
- Newton I: Philosophiae Naturalis Principia Mathematica in 1687
Further reading
- Deemter, Kees van. Not Exactly: In Praise of Vagueness (Oxford University Press; 368 pages; 2010).
Considers vagueness as both a useful and unavoidable aspect of realms from everyday life to computing. - Keefe, R.; Smith, P., eds. (1997). Vagueness: A Reader. MIT Press.
The editors' long introduction gives a clear and very useful overview of theories of vagueness, and they collect many classic papers on the subject. - Keefe, R. 2000. Vagueness. Cambridge: Cambridge University Press.
Technicalities are kept to a minimum to favour a clear account, extremely useful to both students and researchers. - Rick Nouwen; Robert van Rooij; Uli Sauerland; Hans-Christian Schmitz, eds. (Jul 2009). International Workshop on Vagueness in Communication (ViC; held as part of ESSLLI). LNAI. Vol. 6517. Springer. ISBN 978-3-642-18445-1.
- Ronzitti, Giuseppina (ed.), Vagueness: A Guide. Logic, Epistemology, and the Unity of Science, Springer, Dordrecht, 2011.
External links
- "Vagueness" entry in the Stanford Encyclopedia of Philosophy
| Common fallacies (list) | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Formal |
| ||||||||||||||||||||||||||||||||||
| Informal |
| ||||||||||||||||||||||||||||||||||
| Philosophical logic | |
|---|---|
| Critical thinking and informal logic | |
| Theories of deduction | |