| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2018) (Learn how and when to remove this message) |
Given the problem of the aerodynamic design of the nose cone section of any vehicle or body meant to travel through a compressible fluid medium (such as a rocket or aircraft, missile, shell or bullet), an important problem is the determination of the nose cone geometrical shape for optimum performance. For many applications, such a task requires the definition of a solid of revolution shape that experiences minimal resistance to rapid motion through such a fluid medium.
Nose cone shapes and equations
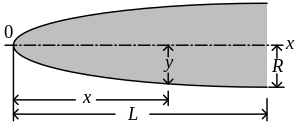
General dimensions
In all of the following nose cone shape equations, L is the overall length of the nose cone and R is the radius of the base of the nose cone. y is the radius at any point x, as x varies from 0, at the tip of the nose cone, to L. The equations define the two-dimensional profile of the nose shape. The full body of revolution of the nose cone is formed by rotating the profile around the centerline C⁄L. While the equations describe the "perfect" shape, practical nose cones are often blunted or truncated for manufacturing, aerodynamic, or thermodynamic reasons.
Conic

 Conic nose cone render and profile with parameters shown.
Conic nose cone render and profile with parameters shown.
A very common nose-cone shape is a simple cone. This shape is often chosen for its ease of manufacture. More optimal, streamlined shapes (described below) are often much more difficult to create. The sides of a conic profile are straight lines, so the diameter equation is simply:
Cones are sometimes defined by their half angle, φ:
- and
Spherically blunted conic

 Spherically blunted conic nose cone render and profile with parameters shown.
Spherically blunted conic nose cone render and profile with parameters shown.
In practical applications such as re-entry vehicles, a conical nose is often blunted by capping it with a segment of a sphere. The tangency point where the sphere meets the cone can be found, using similar triangles, from:
where rn is the radius of the spherical nose cap.
The center of the spherical nose cap, xo, can be found from:
And the apex point, xa can be found from:
Bi-conic
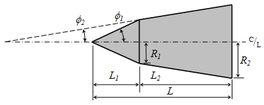
 Bi-conic nose cone render and profile with parameters shown.
Bi-conic nose cone render and profile with parameters shown.
A bi-conic nose cone shape is simply a cone with length L1 stacked on top of a frustum of a cone (commonly known as a conical transition section shape) with length L2, where the base of the upper cone is equal in radius R1 to the top radius of the smaller frustum with base radius R2.
- For :
- For :
Half angles:
- and
- and
Tangent ogive

 Tangent ogive nose cone render and profile with parameters and ogive circle shown.
Tangent ogive nose cone render and profile with parameters and ogive circle shown.
Next to a simple cone, the tangent ogive shape is the most familiar in hobby rocketry. The profile of this shape is formed by a segment of a circle such that the rocket body is tangent to the curve of the nose cone at its base, and the base is on the radius of the circle. The popularity of this shape is largely due to the ease of constructing its profile, as it is simply a circular section.
The radius of the circle that forms the ogive is called the ogive radius, ρ, and it is related to the length and base radius of the nose cone as expressed by the formula:
The radius y at any point x, as x varies from 0 to L is:
The nose cone length, L, must be less than or equal to ρ. If they are equal, then the shape is a hemisphere.
Spherically blunted tangent ogive

 Spherically blunted tangent ogive nose cone render and profile with parameters shown.
Spherically blunted tangent ogive nose cone render and profile with parameters shown.
A tangent ogive nose is often blunted by capping it with a segment of a sphere. The tangency point where the sphere meets the tangent ogive can be found from:
where rn is the radius and xo is the center of the spherical nose cap.
Secant ogive

 Secant ogive nose cone render and profile with parameters and ogive circle shown.
Secant ogive nose cone render and profile with parameters and ogive circle shown.

 Alternate secant ogive render and profile which show a bulge due to a smaller radius.
Alternate secant ogive render and profile which show a bulge due to a smaller radius.
The profile of this shape is also formed by a segment of a circle, but the base of the shape is not on the radius of the circle defined by the ogive radius. The rocket body will not be tangent to the curve of the nose at its base. The ogive radius ρ is not determined by R and L (as it is for a tangent ogive), but rather is one of the factors to be chosen to define the nose shape. If the chosen ogive radius of a secant ogive is greater than the ogive radius of a tangent ogive with the same R and L, then the resulting secant ogive appears as a tangent ogive with a portion of the base truncated.
- and
Then the radius y at any point x as x varies from 0 to L is:
If the chosen ρ is less than the tangent ogive ρ and greater than half the length of the nose cone, then the result will be a secant ogive that bulges out to a maximum diameter that is greater than the base diameter. A classic example of this shape is the nose cone of the Honest John.
Elliptical

 Elliptical nose cone render and profile with parameters shown.
Elliptical nose cone render and profile with parameters shown.
The profile of this shape is one-half of an ellipse, with the major axis being the centerline and the minor axis being the base of the nose cone. A rotation of a full ellipse about its major axis is called a prolate spheroid, so an elliptical nose shape would properly be known as a prolate hemispheroid. This shape is popular in subsonic flight (such as model rocketry) due to the blunt nose and tangent base. This is not a shape normally found in professional rocketry, which almost always flies at much higher velocities where other designs are more suitable. If R equals L, this is a hemisphere.
Parabolic
 Half (K′ = 1/2)
Half (K′ = 1/2) Three-quarter (K′ = 3/4)
Three-quarter (K′ = 3/4) Full (K′ = 1)Renders of common parabolic nose cone shapes.
Full (K′ = 1)Renders of common parabolic nose cone shapes.
This nose shape is not the blunt shape that is envisioned when people commonly refer to a "parabolic" nose cone. The parabolic series nose shape is generated by rotating a segment of a parabola around a line parallel to its latus rectum. This construction is similar to that of the tangent ogive, except that a parabola is the defining shape rather than a circle. Just as it does on an ogive, this construction produces a nose shape with a sharp tip. For the blunt shape typically associated with a parabolic nose, see power series below. (The parabolic shape is also often confused with the elliptical shape.)
For :
K′ can vary anywhere between 0 and 1, but the most common values used for nose cone shapes are:
| Parabola type | K′ value |
|---|---|
| Cone | 0 |
| Half | 1/2 |
| Three quarter | 3/4 |
| Full | 1 |
For the case of the full parabola (K′ = 1) the shape is tangent to the body at its base, and the base is on the axis of the parabola. Values of K′ less than 1 result in a slimmer shape, whose appearance is similar to that of the secant ogive. The shape is no longer tangent at the base, and the base is parallel to, but offset from, the axis of the parabola.
Power series
 |
 Half (n = 1/2) Half (n = 1/2) Three-quarter (n = 3/4) Three-quarter (n = 3/4)
|
The power series includes the shape commonly referred to as a "parabolic" nose cone, but the shape correctly known as a parabolic nose cone is a member of the parabolic series (described above). The power series shape is characterized by its (usually) blunt tip, and by the fact that its base is not tangent to the body tube. There is always a discontinuity at the joint between nose cone and body that looks distinctly non-aerodynamic. The shape can be modified at the base to smooth out this discontinuity. Both a flat-faced cylinder and a cone are members of the power series.
The power series nose shape is generated by rotating the y = R(x/L) curve about the x-axis for values of n less than 1. The factor n controls the bluntness of the shape. For values of n above about 0.7, the tip is fairly sharp. As n decreases towards zero, the power series nose shape becomes increasingly blunt.
- For :
Common values of n include:
| Power type | n value |
|---|---|
| Cylinder | 0 |
| Half (parabola) | 1/2 |
| Three quarter | 3/4 |
| Cone | 1 |
Haack series
 |
 LD-Haack (Von Kármán) (C = 0) LD-Haack (Von Kármán) (C = 0) LV-Haack (C = 1/3) LV-Haack (C = 1/3)
|
Unlike all of the nose cone shapes above, Wolfgang Haack's series shapes are not constructed from geometric figures. The shapes are instead mathematically derived for the purpose of minimizing drag; a related shape with similar derivation being the Sears–Haack body. While the series is a continuous set of shapes determined by the value of C in the equations below, two values of C have particular significance: when C = 0, the notation LD signifies minimum drag for the given length and diameter, and when C = 1/3, LV indicates minimum drag for a given length and volume. The Haack series nose cones are not perfectly tangent to the body at their base except for the case where C = 2/3. However, the discontinuity is usually so slight as to be imperceptible. For C > 2/3, Haack nose cones bulge to a maximum diameter greater than the base diameter. Haack nose tips do not come to a sharp point, but are slightly rounded.
Special values of C (as described above) include:
| Haack series type | C value |
|---|---|
| LD-Haack (Von Kármán) | 0 |
| LV-Haack | 1/3 |
| Tangent | 2/3 |
Von Kármán
The Haack series designs giving minimum drag for the given length and diameter, the LD-Haack where C = 0, is commonly called the Von Kármán or Von Kármán ogive.
Aerospike
Main article: Drag-reducing aerospike
An aerospike can be used to reduce the forebody pressure acting on supersonic aircraft. The aerospike creates a detached shock ahead of the body, thus reducing the drag acting on the aircraft.
Nose cone drag characteristics
For aircraft and rockets, below Mach .8, the nose pressure drag is essentially zero for all shapes. The major significant factor is friction drag, which is largely dependent upon the wetted area, the surface smoothness of that area, and the presence of any discontinuities in the shape. For example, in strictly subsonic rockets a short, blunt, smooth elliptical shape is usually best. In the transonic region and beyond, where the pressure drag increases dramatically, the effect of nose shape on drag becomes highly significant. The factors influencing the pressure drag are the general shape of the nose cone, its fineness ratio, and its bluffness ratio.
Influence of the general shape

Many references on nose cone design contain empirical data comparing the drag characteristics of various nose shapes in different flight regimes. The chart shown here seems to be the most comprehensive and useful compilation of data for the flight regime of greatest interest. This chart generally agrees with more detailed, but less comprehensive data found in other references (most notably the USAF Datcom).
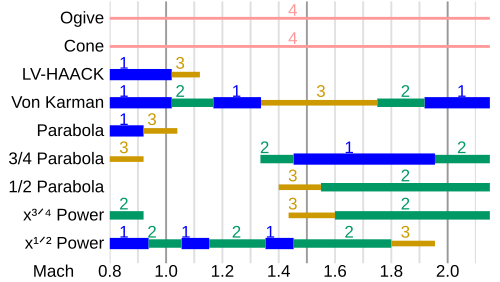
In many nose cone designs, the greatest concern is flight performance in the transonic region from Mach 0.8 to Mach 1.2. Although data are not available for many shapes in the transonic region, the table clearly suggests that either the Von Kármán shape, or power series shape with n = 1/2, would be preferable to the popular conical or ogive shapes, for this purpose.

This observation goes against the often-repeated conventional wisdom that a conical nose is optimum for "Mach-breaking". Fighter aircraft are probably good examples of nose shapes optimized for the transonic region, although their nose shapes are often distorted by other considerations of avionics and inlets. For example, an F-16 Fighting Falcon nose appears to be a very close match to a Von Kármán shape.
Influence of the fineness ratio
The ratio of the length of a nose cone compared to its base diameter is known as the fineness ratio. This is sometimes also called the aspect ratio, though that term is usually applied to wings and tails. Fineness ratio is often applied to the entire vehicle, considering the overall length and diameter. The length/diameter relation is also often called the caliber of a nose cone.
At supersonic speeds, the fineness ratio has a significant effect on nose cone wave drag, particularly at low ratios; but there is very little additional gain for ratios increasing beyond 5:1. As the fineness ratio increases, the wetted area, and thus the skin friction component of drag, will also increase. Therefore, the minimum drag fineness ratio will ultimately be a trade-off between the decreasing wave drag and increasing friction drag.
See also
Further reading
- Haack, Wolfgang (1941). "Geschoßformen kleinsten Wellenwiderstandes" (PDF). Bericht 139 der Lilienthal-Gesellschaft für Luftfahrtforschung: 14–28. Archived from the original (PDF) on 2007-09-27.
- U.S. Army Missile Command (17 July 1990). Design of Aerodynamically Stabilized Free Rockets. U.S. Government Printing Office. MIL-HDBK-762(MI).
References
- ^ satyajit panigrahy (August 2020). "IMPROVEMENT OF FIRE POWER OF WEAPON SYSTEM BY OPTIMIZING NOSE CONE SHAPE AND WAR HEAD GROUPING". ResearchGate. doi:10.13140/RG.2.2.28694.36161.
- Crowell Sr., Gary A. (1996). The Descriptive Geometry of Nose Cones (PDF) (Report). Archived from the original (PDF) on 11 April 2011. Retrieved 11 April 2011.
- Iyer, Aditya Rajan; Pant, Anjali (August 2020). "A Review on Nose Cone Designs for Different Flight Regimes" (PDF). International Research Journal of Engineering and Technology. 7 (8): 3546–3554. S2CID 221684654.
- Chin, S. S. (1961). Missile Configuration Design. New York City: McGraw-Hill. LCCN 60-15518. OCLC 253099252.

 and
and 





 :
: 
 :
: 
 and
and 
 and
and 



 and
and 



 :
: 
 :
: 
