In machine learning, the term tensor informally refers to two different concepts (i) a way of organizing data and (ii) a multilinear (tensor) transformation. Data may be organized in a multidimensional array (M-way array), informally referred to as a "data tensor"; however, in the strict mathematical sense, a tensor is a multilinear mapping over a set of domain vector spaces to a range vector space. Observations, such as images, movies, volumes, sounds, and relationships among words and concepts, stored in an M-way array ("data tensor"), may be analyzed either by artificial neural networks or tensor methods.
Tensor decomposition factorizes data tensors into smaller tensors. Operations on data tensors can be expressed in terms of matrix multiplication and the Kronecker product. The computation of gradients, a crucial aspect of backpropagation, can be performed using software libraries such as PyTorch and TensorFlow.
Computations are often performed on graphics processing units (GPUs) using CUDA, and on dedicated hardware such as Google's Tensor Processing Unit or Nvidia's Tensor core. These developments have greatly accelerated neural network architectures, and increased the size and complexity of models that can be trained.
History
A tensor is by definition a multilinear map. In mathematics, this may express a multilinear relationship between sets of algebraic objects. In physics, tensor fields, considered as tensors at each point in space, are useful in expressing mechanics such as stress or elasticity. In machine learning, the exact use of tensors depends on the statistical approach being used.
In 2001, the field of signal processing and statistics were making use of tensor methods. Pierre Comon surveys the early adoption of tensor methods in the fields of telecommunications, radio surveillance, chemometrics and sensor processing. Linear tensor rank methods (such as, Parafac/CANDECOMP) analyzed M-way arrays ("data tensors") composed of higher order statistics that were employed in blind source separation problems to compute a linear model of the data. He noted several early limitations in determining the tensor rank and efficient tensor rank decomposition.
In the early 2000s, multilinear tensor methods crossed over into computer vision, computer graphics and machine learning with papers by Vasilescu or in collaboration with Terzopoulos, such as Human Motion Signatures, TensorFaces TensorTexures and Multilinear Projection. Multilinear algebra, the algebra of higher-order tensors, is a suitable and transparent framework for analyzing the multifactor structure of an ensemble of observations and for addressing the difficult problem of disentangling the causal factors based on second order or higher order statistics associated with each causal factor.
Tensor (multilinear) factor analysis disentangles and reduces the influence of different causal factors with multilinear subspace learning. When treating an image or a video as a 2- or 3-way array, i.e., "data matrix/tensor", tensor methods reduce spatial or time redundancies as demonstrated by Wang and Ahuja.
Yoshua Bengio, Geoff Hinton and their collaborators briefly discuss the relationship between deep neural networks and tensor factor analysis beyond the use of M-way arrays ("data tensors") as inputs. One of the early uses of tensors for neural networks appeared in natural language processing. A single word can be expressed as a vector via Word2vec. Thus a relationship between two words can be encoded in a matrix. However, for more complex relationships such as subject-object-verb, it is necessary to build higher-dimensional networks. In 2009, the work of Sutskever introduced Bayesian Clustered Tensor Factorization to model relational concepts while reducing the parameter space. From 2014 to 2015, tensor methods become more common in convolutional neural networks (CNNs). Tensor methods organize neural network weights in a "data tensor", analyze and reduce the number of neural network weights. Lebedev et al. accelerated CNN networks for character classification (the recognition of letters and digits in images) by using 4D kernel tensors.
Definition
Let be a field such as the real numbers or the complex numbers . A tensor is a multilinear transformation from a set of domain vector spaces to a range vector space:
Here, and are positive integers, and is the number of modes of a tensor (also known as the number of ways of a multi-way array). The dimensionality of mode is , for .

In statistics and machine learning, an image is vectorized when viewed as a single observation, and a collection of vectorized images is organized as a "data tensor". For example, a set of facial images with pixels that are the consequences of multiple causal factors, such as a facial geometry , an expression , an illumination condition , and a viewing condition may be organized into a data tensor (ie. multiway array) where are the total number of facial geometries, are the total number of expressions, are the total number of illumination conditions, and are the total number of viewing conditions. Tensor factorizations methods such as TensorFaces and multilinear (tensor) independent component analysis factorizes the data tensor into a set of vector spaces that span the causal factor representations, where an image is the result of tensor transformation that maps a set of causal factor representations to the pixel space.

Another approach to using tensors in machine learning is to embed various data types directly. For example, a grayscale image, commonly represented as a discrete 2-way array with dimensionality where are the number of rows and are the number of columns. When a an image is treated as 2-way array or 2nd order tensor (ie as a collection of column/row observations), tensor factorization methods compute the image column space, the image row space and the normalized PCA coeficients or the ICA coefficients.
Similarly, a color image with RGB channels, may be viewed as a 3rd order data tensor or 3-way array.--------
In natural language processing, a word might be expressed as a vector via the Word2vec algorithm. Thus becomes a mode-1 tensor
The embedding of subject-object-verb semantics requires embedding relationships among three words. Because a word is itself a vector, subject-object-verb semantics could be expressed using mode-3 tensors
In practice the neural network designer is primarily concerned with the specification of embeddings, the connection of tensor layers, and the operations performed on them in a network. Modern machine learning frameworks manage the optimization, tensor factorization and backpropagation automatically.
As unit values

Tensors may be used as the unit values of neural networks which extend the concept of scalar, vector and matrix values to multiple dimensions.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the activation function :
where

If each output element of is a scalar, then we have the classical definition of an artificial neural network. By replacing each unit component with a tensor, the network is able to express higher dimensional data such as images or videos:
This use of tensors to replace unit values is common in convolutional neural networks where each unit might be an image processed through multiple layers. By embedding the data in tensors such network structures enable learning of complex data types.
In fully connected layers
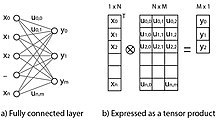
Tensors may also be used to compute the layers of a fully connected neural network, where the tensor is applied to the entire layer instead of individual unit values.
The output value of single layer unit is the sum-product of its input units and the connection weights filtered through the activation function :
The vectors and of output values can be expressed as a mode-1 tensors, while the hidden weights can be expressed as a mode-2 tensor. In this example the unit values are scalars while the tensor takes on the dimensions of the network layers:
In this notation, the output values can be computed as a tensor product of the input and weight tensors:
which computes the sum-product as a tensor multiplication (similar to matrix multiplication).
This formulation of tensors enables the entire layer of a fully connected network to be efficiently computed by mapping the units and weights to tensors.
In convolutional layers
A different reformulation of neural networks allows tensors to express the convolution layers of a neural network. A convolutional layer has multiple inputs, each of which is a spatial structure such as an image or volume. The inputs are convolved by filtering before being passed to the next layer. A typical use is to perform feature detection or isolation in image recognition.
Convolution is often computed as the multiplication of an input signal with a filter kernel . In two dimensions the discrete, finite form is:
where is the width of the kernel.
This definition can be rephrased as a matrix-vector product in terms of tensors that express the kernel, data and inverse transform of the kernel.
where and are the inverse transform, data and kernel. The derivation is more complex when the filtering kernel also includes a non-linear activation function such as sigmoid or ReLU.
The hidden weights of the convolution layer are the parameters to the filter. These can be reduced with a pooling layer which reduces the resolution (size) of the data, and can also be expressed as a tensor operation.
Tensor factorization
An important contribution of tensors in machine learning is the ability to factorize tensors to decompose data into constituent factors or reduce the learned parameters. Data tensor modeling techniques stem from the linear tensor decomposition (CANDECOMP/Parafac decomposition) and the multilinear tensor decompositions (Tucker).
Tucker decomposition

Tucker decomposition, for example, takes a 3-way array and decomposes the tensor into three matrices and a smaller tensor . The shape of the matrices and new tensor are such that the total number of elements is reduced. The new tensors have shapes
Then the original tensor can be expressed as the tensor product of these four tensors:
In the example shown in the figure, the dimensions of the tensors are
- : I=8, J=6, K=3, : I=8, P=5, : J=6, Q=4, : K=3, R=2, : P=5, Q=4, R=2.
The total number of elements in the Tucker factorization is
The number of elements in the original is 144, resulting in a data reduction from 144 down to 110 elements, a reduction of 23% in parameters or data size. For much larger initial tensors, and depending on the rank (redundancy) of the tensor, the gains can be more significant.
The work of Rabanser et al. provides an introduction to tensors with more details on the extension of Tucker decomposition to N-dimensions beyond the mode-3 example given here.
Tensor trains
Another technique for decomposing tensors rewrites the initial tensor as a sequence (train) of smaller sized tensors. A tensor-train (TT) is a sequence of tensors of reduced rank, called canonical factors. The original tensor can be expressed as the sum-product of the sequence.
Developed in 2011 by Ivan Oseledts, the author observes that Tucker decomposition is "suitable for small dimensions, especially for the three-dimensional case. For large d it is not suitable." Thus tensor-trains can be used to factorize larger tensors in higher dimensions.
Tensor graphs
The unified data architecture and automatic differentiation of tensors has enabled higher-level designs of machine learning in the form of tensor graphs. This leads to new architectures, such as tensor-graph convolutional networks (TGCN), which identify highly non-linear associations in data, combine multiple relations, and scale gracefully, while remaining robust and performant.
These developments are impacting all areas of machine learning, such as text mining and clustering, time varying data, and neural networks wherein the input data is a social graph and the data changes dynamically.
Hardware
Tensors provide a unified way to train neural networks for more complex data sets. However, training is expensive to compute on classical CPU hardware.
In 2014, Nvidia developed cuDNN, CUDA Deep Neural Network, a library for a set of optimized primitives written in the parallel CUDA language. CUDA and thus cuDNN run on dedicated GPUs that implement unified massive parallelism in hardware. These GPUs were not yet dedicated chips for tensors, but rather existing hardware adapted for parallel computation in machine learning.
In the period 2015–2017 Google invented the Tensor Processing Unit (TPU). TPUs are dedicated, fixed function hardware units that specialize in the matrix multiplications needed for tensor products. Specifically, they implement an array of 65,536 multiply units that can perform a 256x256 matrix sum-product in just one global instruction cycle.
Later in 2017, Nvidia released its own Tensor Core with the Volta GPU architecture. Each Tensor Core is a microunit that can perform a 4x4 matrix sum-product. There are eight tensor cores for each shared memory (SM) block. The first GV100 GPU card has 108 SMs resulting in 672 tensor cores. This device accelerated machine learning by 12x over the previous Tesla GPUs. The number of tensor cores scales as the number of cores and SM units continue to grow in each new generation of cards.
The development of GPU hardware, combined with the unified architecture of tensor cores, has enabled the training of much larger neural networks. In 2022, the largest neural network was Google's PaLM with 540 billion learned parameters (network weights) (the older GPT-3 language model has over 175 billion learned parameters that produces human-like text; size isn't everything, Stanford's much smaller 2023 Alpaca model claims to be better, having learned from Meta/Facebook's 2023 model LLaMA, the smaller 7 billion parameter variant). The widely popular chatbot ChatGPT is built on top of GPT-3.5 (and after an update GPT-4) using supervised and reinforcement learning.
References
- ^ Vasilescu, MAO; Terzopoulos, D (2007). "Multilinear (tensor) image synthesis, analysis, and recognition [exploratory dsp]" (PDF). IEEE Signal Processing Magazine. 24 (6): 118–123. Bibcode:2007ISPM...24R.118V. doi:10.1109/MSP.2007.906024.
- Vasilescu, MAO (2009), A Multilinear (Tensor) Algebraic Framework for Computer Graphics, Computer Vision, and Machine Learning (PDF), University of Toronto
- Kolda, Tamara G.; Bader, Brett W. (2009-08-06). "Tensor Decompositions and Applications". SIAM Review. 51 (3): 455–500. Bibcode:2009SIAMR..51..455K. doi:10.1137/07070111X. ISSN 0036-1445. S2CID 16074195.
- Sidiropoulos, Nicholas D.; De Lathauwer, Lieven; Fu, Xiao; Huang, Kejun; Papalexakis, Evangelos E.; Faloutsos, Christos (2017-07-01). "Tensor Decomposition for Signal Processing and Machine Learning". IEEE Transactions on Signal Processing. 65 (13): 3551–3582. arXiv:1607.01668. Bibcode:2017ITSP...65.3551S. doi:10.1109/TSP.2017.2690524. ISSN 1053-587X. S2CID 16321768.
- ^ Rabanser, Stephan (2017). "Introduction to Tensor Decompositions and their Applications in Machine Learning". arXiv:1711.10781 .
- Sidiropoulous, N (2016). "Tensor Decomposition for Signal Processing and Machine Learning". IEEE Transactions on Signal Processing. 65 (13).
- Grout, I (2018). "Hardware Considerations for Tensor Implementation and Analysis Using the Field Programmable Gate Array". Electronics. 7 (320): 320. doi:10.3390/electronics7110320. hdl:10344/7368.
- Paszke, A (2019). "PyTorch: An Imperative Style, High-Performance Deep Learning Library". Proceedings of the 33rd International Conference on Neural Information Processing Systems: 8026–037. arXiv:1912.01703.
- Adabi, M (2016). "TensorFlow: A System for Large-Scale Machine Learning" (PDF). Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation. arXiv:1605.08695.
- Comon, Pierre (2001), "Tensor Decompositions: State of the Art and Applications", Mathematics in Signal Processing, Oxford University Press
- Vasilescu, M.A.O.; Shashua, Amnon (2007), Tensor Methods for Machine Learning, Computer Vision, and Computer Graphics Tutorial, International Conference on Machine Learning
- Vasilescu, M.A.O. (2002), Human Motion Signatures: Analysis, Synthesis, Recognition, vol. 3, Proceedings of International Conference on Pattern Recognition (ICPR 2002), pp. 456–460
- Vasilescu, M.A.O. (2001), An Algorithm for Extracting Human Motion Signatures, Computer Vision and Pattern Recognition CVPR 2001 Technical Sketches
- ^ Vasilescu, M.A.O.; Terzopoulos, D. (2002). Multilinear Analysis of Image Ensembles: TensorFaces (PDF). Lecture Notes in Computer Science 2350; (Presented at Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark). Springer, Berlin, Heidelberg. doi:10.1007/3-540-47969-4_30. ISBN 9783540437451.
- ^ Vasilescu, M.A.O.; Terzopoulos, D. (2005), Multilinear Independent Component Analysis (PDF), LProceedings of the 2005 IEEE Computer Vision and Pattern Recognition Conference (CVPR 2005), San Diego, CA
- Vasilescu, M.A.O.; Terzopoulos, D. (2004), "TensorTextures: Multilinear Image-Based Rendering" (PDF), ACM Transactions on Graphics, vol. 23, no. 3, pp. 336–342, doi:10.1145/1015706.1015725
- Vasilescu, M.A.O. (2011). Multilinear Projection for Face Recognition via Canonical Decomposition. In Proc. Face and Gesture Conference (FG'11). pp. 476–483.
- Vasilescu, M.A.O.; Terzopoulos, D. (2007), "Multilinear Projection for Appearance-Based Recognition in the Tensor Framework", Proc. Eleventh IEEE International Conf. on Computer Vision (ICCV'07), pp. 1–8
- Vasilescu, M.A.O.; Terzopoulos, D. (2003), "Multilinear Subspace Learning of Image Ensembles", 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003. Proceedings.
- Wang, H; Narendra, Ahuja (2005), Rank-R approximation of tensors using image-as-matrix representation, IEEE Computer Society Conference on Computer Vision and Pattern Recognition
- Desjardins, Guillaume; Courvile, Aaron; Bengio, Yoshua (2012). "Disentangling Factors of Variation via Generative Entangling". arXiv:1210.5474 .
- Bengio, Yoshua; Courville, Aaron (2013). "Disentangling Factors of Variation via Generative Entangling". Handbook on Neural Information Processing: 1–28. ISBN 9783642366574.
- Tang, Yichuan; Salakhutdinov, Ruslan; Hinton, Geoffrey (2013). "Tensor Analyzers" (PDF). 30 Th International Conference on Machine Learning.
- Memisevic, Roland; Hinton, Geoffrey (2010). "Learning to Represent Spatial Transformations with Factored Higher-Order Boltzmann Machines" (PDF). Neural Computation. 22 (6): 1473–1492. doi:10.1162/neco.2010.01-09-953. PMID 20141471. S2CID 1413690.
- Sutskever, I (2009). "Modeling Relational Data using Bayesian Clustered Tensor Factorization". Advances in Neural Information Processing Systems. 22.
- Novikov, A; Dmitry, P; Osokin, A; Vetrov, D (2015), "Tensorizing Neural Networks", Neural Information Processing Systems, arXiv:1509.06569
- Kossaifi, Jean (2019). "T-Net: Parameterizing Fully Convolutional Nets with a Single High-Order Tensor". arXiv:1904.02698 .
- Lebedev, Vadim (2014), Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition, arXiv:1412.6553
- Vasilescu, M. Alex O. (2009), A Multilinear (Tensor) Framework for Computer Graphics, Computer Vision and Machine Learning" (PDF)
- ^ Vasilescu, M. Alex O (2024). ""Causal Deep Learning"". arXiv:2301.00314.
- Bedden, David (2017). "Deep Tensor Convolution on Multicores". arXiv:1611.06565 .
- Oseledets, Ivan (2011). "Tensor-Train Decomposition". SIAM Journal on Scientific Computing. 33 (5): 2295–2317. Bibcode:2011SJSC...33.2295O. doi:10.1137/090752286. S2CID 207059098.
- Ioannidis, Vassilis (2020). "Tensor Graph Convolutional Networks for Multi-Relational and Robust Learning". IEEE Transactions on Signal Processing. 68: 6535–6546. arXiv:2003.07729. Bibcode:2020ITSP...68.6535I. doi:10.1109/TSP.2020.3028495. S2CID 212736801.
- Boutalbi, Rafika (2022). "Tensor-based Graph Modularity for Text Data Clustering". Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval.
- Malik, Osman (2019). "Tensor Graph Neural Networks for Learning on Time Varying Graphs". 2019 Conference on Neural Information Processing (NeurIPS).
- Manessi, Franco; Rozza, Alessandro; Manzo, Mario (2020). "Dynamic graph convolutional networks". Pattern Recognition. 97: 107000. arXiv:1704.06199. Bibcode:2020PatRe..9707000M. doi:10.1016/j.patcog.2019.107000. S2CID 16745566.
- Malik, Osman. "Dynamic Graph Convolutional Networks Using the Tensor M-Product".
- Serrano, Jerome (2014). "Nvidia Introduces cuDNN, a CUDA-based library for Deep Neural Networks".
- Jouppi, Norman; Young; Patil; Patterson (2018). "Motivation for and evaluation of the first tensor processing unit". IEEE Micro. 38 (3): 10–19. doi:10.1109/MM.2018.032271057. S2CID 21657842.
- Hemsoth, Nicole (2017). "First In-Depth Look at Google's TPU Architecture". The Next Platform.
- "NVIDIA Tesla V100 GPU Architecture" (PDF). 2017.
- Armasu, Lucian (2017). "On Tensors, Tensorflow, And Nvidia's Latest 'Tensor Cores'".
- "Pathways Language Model (PaLM): Scaling to 540 Billion Parameters for Breakthrough Performance". ai.googleblog.com. Retrieved 2023-03-29.
- "Alpaca: A Strong, Replicable Instruction-Following Model". crfm.stanford.edu. Retrieved 2023-03-29.
 be a
be a  or the
or the  . A tensor
. A tensor  is a multilinear transformation from a set of domain vector spaces to a range vector space:
is a multilinear transformation from a set of domain vector spaces to a range vector space:

 and
and  are positive integers, and
are positive integers, and  is the number of modes of a tensor (also known as the number of ways of a multi-way array). The dimensionality of mode
is the number of modes of a tensor (also known as the number of ways of a multi-way array). The dimensionality of mode  is
is  , for
, for  .
.
 is the result of a tensor transformation
is the result of a tensor transformation  that maps a set of causal factor representations to the pixel space. Tensor factorization methods, such as the M-mode SVD or the M-mode ICA, factorize a data tensor composed of a collection of vectorized images and learn a set vector spaces (
that maps a set of causal factor representations to the pixel space. Tensor factorization methods, such as the M-mode SVD or the M-mode ICA, factorize a data tensor composed of a collection of vectorized images and learn a set vector spaces ( ) that span the causal factor representations and a tensor transformation
) that span the causal factor representations and a tensor transformation  with
with  pixels that are the consequences of multiple causal factors, such as a facial geometry
pixels that are the consequences of multiple causal factors, such as a facial geometry  , an expression
, an expression  , an illumination condition
, an illumination condition  , and a viewing condition
, and a viewing condition  may be organized into a data tensor (ie. multiway array)
may be organized into a data tensor (ie. multiway array)  where
where  are the total number of facial geometries,
are the total number of facial geometries,  are the total number of expressions,
are the total number of expressions,  are the total number of illumination conditions, and
are the total number of illumination conditions, and  are the total number of viewing conditions. Tensor factorizations methods such as TensorFaces and multilinear (tensor) independent component analysis factorizes the data tensor into a set of vector spaces that span the causal factor representations, where an image is the result of tensor transformation
are the total number of viewing conditions. Tensor factorizations methods such as TensorFaces and multilinear (tensor) independent component analysis factorizes the data tensor into a set of vector spaces that span the causal factor representations, where an image is the result of tensor transformation  with dimensionality
with dimensionality  where
where  are the number of rows and
are the number of rows and  are the number of columns. When a an image is treated as 2-way array or 2nd order tensor (ie as a collection of column/row observations), tensor factorization methods compute the image column space, the image row space and the normalized PCA coeficients or the ICA coefficients.
are the number of columns. When a an image is treated as 2-way array or 2nd order tensor (ie as a collection of column/row observations), tensor factorization methods compute the image column space, the image row space and the normalized PCA coeficients or the ICA coefficients.
 may be viewed as a 3rd order data tensor or 3-way array.--------
may be viewed as a 3rd order data tensor or 3-way array.--------
 via the
via the 

 is the sum-product of its input units and the connection weights filtered through the
is the sum-product of its input units and the connection weights filtered through the  :
:




 and
and  of output values can be expressed as a mode-1 tensors, while the hidden weights can be expressed as a mode-2 tensor. In this example the unit values are scalars while the tensor takes on the dimensions of the network layers:
of output values can be expressed as a mode-1 tensors, while the hidden weights can be expressed as a mode-2 tensor. In this example the unit values are scalars while the tensor takes on the dimensions of the network layers:




 with a filter kernel
with a filter kernel 
 is the width of the kernel.
is the width of the kernel.

 and
and  are the inverse transform, data and kernel. The derivation is more complex when the filtering kernel also includes a non-linear activation function such as sigmoid or ReLU.
are the inverse transform, data and kernel. The derivation is more complex when the filtering kernel also includes a non-linear activation function such as sigmoid or ReLU.
 and decomposes the tensor into three matrices
and decomposes the tensor into three matrices  and a smaller tensor
and a smaller tensor  . The shape of the matrices and new tensor are such that the total number of elements is reduced. The new tensors have shapes
. The shape of the matrices and new tensor are such that the total number of elements is reduced. The new tensors have shapes





 : I=8, J=6, K=3,
: I=8, J=6, K=3,  : I=8, P=5,
: I=8, P=5,  : J=6, Q=4,
: J=6, Q=4, 

