The rare disease assumption is a mathematical assumption in epidemiologic case-control studies where the hypothesis tests the association between an exposure and a disease. It is assumed that, if the prevalence of the disease is low, then the odds ratio (OR) approaches the relative risk (RR). The idea was first demonstrated by Jerome Cornfield.
Case control studies are relatively inexpensive and less time-consuming than cohort studies. Since case control studies don't track patients over time, they can't establish relative risk. The case control study can, however, calculate the exposure-odds ratio, which, mathematically, is supposed to approach the relative risk as prevalence falls.
Sander Greenland showed that if the prevalence is 10% or less, the disease can be considered rare enough to allow the rare disease assumption. Unfortunately, the magnitude of discrepancy between the odds ratio and the relative risk is dependent not only on the prevalence, but also, to a great degree, on two other factors. Thus, the reliance on the rare disease assumption when discussing odds ratios as risk should be explicitly stated and discussed.
Mathematical proof
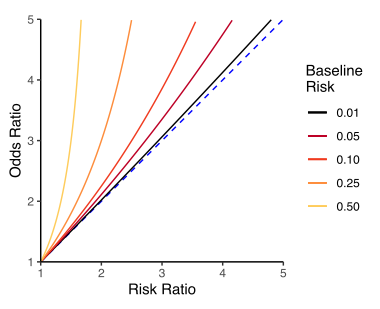
The rare disease assumption can be demonstrated mathematically using the definitions for relative risk and odds ratio.
| Disease Positive | Disease Negative | |
|---|---|---|
| Exposure | a | b |
| No Exposure | c | d |
With regards to the table above,
and
As prevalence decreases, the number of positive cases decreases. As approaches 0, then and , individually, also approaches 0. In other words, as approaches 0,
.
Examples
The following example illustrates one of the problems, which occurs when the effects are large because the disease is common in the exposed or unexposed group. Consider the following contingency table.
| Disease Positive | Disease Negative | |
|---|---|---|
| Exposure | 4 | 6 |
| No Exposure | 5 | 85 |
and
While the prevalence is only 9% (9/100), the odds ratio (OR) is equal to 11.3 and the relative risk (RR) is equal to 7.2. Despite fulfilling the rare disease assumption overall, the OR and RR can hardly be considered to be approximately the same. However, the prevalence in the exposed group is 40%, which means is not sufficiently small compared to and therefore .
| Disease Positive | Disease Negative | |
|---|---|---|
| Exposure | 4 | 96 |
| No Exposure | 5 | 895 |
and
With a prevalence of 0.9% (9/1000) and no changes to the effect size (same RR as above), estimates for RR and OR converge. Sometimes the prevalence threshold for which the rare disease assumption holds may be much lower.
References
- ^ Cornfield, Jerome (1951-06-01). "A Method of Estimating Comparative Rates from Clinical Data. Applications to Cancer of the Lung, Breast, and Cervix". JNCI: Journal of the National Cancer Institute. doi:10.1093/jnci/11.6.1269. ISSN 1460-2105.
- Greenland, Sander; Thomas, D. C. (1982). "On the need for the rare disease assumption in case-control studies". American Journal of Epidemiology. 116 (3): 547–553. doi:10.1093/oxfordjournals.aje.a113439. ISSN 0002-9262. PMID 7124721.
- Greenland, S.; Thomas, D. C.; Morgenstern, H. (1986). "The rare-disease assumption revisited. A critique of "estimators of relative risk for case-control studies"". American Journal of Epidemiology. 124 (6): 869–883. doi:10.1093/oxfordjournals.aje.a114476. ISSN 0002-9262. PMID 3776970.
- Knol, Mirjam J.; Vandenbroucke, Jan P.; Scott, Pippa; Egger, Matthias (2008). "What Do Case-Control Studies Estimate? Survey of Methods and Assumptions in Published Case-Control Research". American Journal of Epidemiology. 168 (9): 1073–1081. doi:10.1093/aje/kwn217. PMID 18794220.
- Fletcher, Robert H. (8 January 2013). Clinical epidemiology : the essentials. Fletcher, Suzanne W.,, Fletcher, Grant S. (5th ed.). Philadelphia. ISBN 978-1-4698-2625-7. OCLC 859337100.
{{cite book}}: CS1 maint: location missing publisher (link)
 and
and 
 decreases. As
decreases. As  and
and  , individually, also approaches 0. In other words, as
, individually, also approaches 0. In other words, as  .
.
 and
and 
 and therefore
and therefore  .
.
 and
and 