Thermohaline staircases are patterns that form in oceans and other bodies of salt water, characterised by step-like structures observed in vertical temperature and salinity profiles; the patterns are formed and maintained by double diffusion of heat and salt. The ocean phenomenon consists of well-mixed layers of ocean water stacked on top of each other. The well-mixed layers are separated by high-gradient interfaces, which can be several meters thick. The total thickness of staircases ranges typically from tens to hundreds of meters.
Two types of staircases are distinguished. Salt-fingering staircases can be found at locations where relatively warm, salty water overlies relatively colder, fresher water. Here, large-scale temperature and salinity both increase upward, making the mixing process of salt fingering possible. Locations where you can find these type of staircases are for example beneath the Mediterranean outflow, in the Tyrrhenian Sea, and northeast Caribbean. Diffusive staircases can be found at locations where both temperature and salinity increase downward, for example in the Arctic Ocean and in the Weddell Sea. An important feature of thermohaline staircases is their extreme stability in space and time. They can persist several years or more and can extend for hundreds of kilometers. The interest in thermohaline staircases is partly due to the fact that the staircases represent mixing hot spots in the main thermocline.
Extensive definition and detection

To determine the presence of thermohaline staircases, the following steps can be taken according to the algorithm designed by Van der Boog.
The first step of the algorithm is to identify the mixed layers by locating weak vertical density gradients in conservative temperature and absolute salinity. To do so, the threshold gradient method is used with a threshold of , with the pressure and the reference pressure. The vertical conservative temperature, absolute salinity, and potential density gradients are all below the threshold value by meeting these three conditions:
with the thermal expansion coefficient, the haline contraction coefficient, the reference density, the conservative temperature, and the salinity.
The second step is to define the interface, which is the part of the water column in the middle of two mixed layers. It is required that the conservative temperature, absolute salinity, and potential density variations in the interface should be larger than the variations within each mixed layer to ensure a stepped structure. Therefore the following conditions should be met:
where subscript 1 corresponds to the mixed layer above the interface and subscript 2 corresponds to the mixed layer below the interface.
The third step is to limit the interface height . The interface height should be smaller than the height of the mixed layers directly above and below the interface . This condition has to be met in order to ensure that the interface is relatively thin compared to the mixed layers surrounding it. Furthermore, the algorithm removes all interfaces with conservative temperature or absolute salinity inversions to make sure that it only detects step-like structures that are associated with the presence of thermohaline staircases.
The fourth step is to determine the double-diffusive regime (salt-fingering or diffusive) of each interface. When both conservative temperature and absolute salinity of the mixed layers above and below the interface increase downward, the interface belongs to the diffusive regime. When both conservative temperature and absolute salinity of the mixed layers above and below the interface both increase upward, the interface is classified as the salt-fingering regime.
Finally, only vertical sequences of at least two interfaces in the same double-diffusive regime are selected, where the interfaces should be separated from each other by only one mixed layer. This way, most thermohaline intrusions are removed, as these are characterised by alternating mixed layers in the diffusive and salt-finger regimes. Furthermore, the algorithm removes salt-fingering interfaces and diffusive-convective interfaces outside their favourable Turner angle , a parameter used to describe the local stability of an inviscid water column. Interfaces with salt-fingering characteristics should correspond to Turner angles of and interfaces with diffusive-convective characteristics should correspond to Turner angles of .
Staircase origin
The origin of thermohaline staircases relies on double diffusive convection, and specifically on the fact that heated water diffuses more readily than salty water. However, there is still much debate on which specific mechanism of layering plays a role. Six possible mechanisms are described below.
Collective instability mechanism
This mechanism, involving collective instability, relies on the idea that after a period of active internal wave motion, layers appear. This hypothesis was motivated by laboratory experiments in which staircases formed from the initially uniform temperature and salinity gradients. Growing waves might overturn and generate the stepped structure of thermohaline staircases.
Thermohaline intrusion mechanism
This hypothesis states that staircases represent the final stage in the evolution of thermohaline intrusions. Intrusions can evolve either to a state consisting of alternating salt-finger and diffusive interfaces separated by convecting layers, which is common at high density ratio , or to a series of salt-finger interfaces when the density ratio is low . This proposition relies on the presence of lateral property gradients to drive interleaving. This mechanism, where thermohaline intrusions are transformed into staircases, are likely to exist in strong temperature-salinity fronts.
Metastable equilibria mechanism
A different theory states that staircases represent distinct metastable equilibria. It is suggested that finite amplitude perturbations to the gradient state force the system into a layered regime where it can remain for long periods of time. Large initial perturbations to the gradient state make the transition to the staircase more likely and accelerate the process. Once the staircase is created, the system becomes resilient to further structural changes.
Applied flux mechanism
The applied flux mechanism was mainly tested in laboratory experiments, and is most likely at work in cases when layering is caused by geothermal heating. When a stable salinity gradient is heated from below, top-heavy convection will take place in the lower part of the water column. The well-mixed convecting layer is bounded from above by a thin high-gradient interface. By a combination of molecular diffusion and entrainment across the interface, heat is transferred upward from the convecting layer. The molecular transfer of heat exceeds that of salt, resulting in a supply of buoyancy to the region immediately above the interface. This leads to the formation of a second convecting layer. The process can repeat itself over and over, which results in a sequence of mixed layers separated by sharp interfaces, a thermohaline staircase.
Negative density diffusion
In salt-fingering staircases, vertical temperature and salinity fluxes are downgradient, while the vertical density flux is upgradient. This is explained by the fact that the potential energy released in transporting salt downward must exceed that expended in transporting heat upward, resulting in a net downward transport of mass. This negative diffusion sharpens the fluctuations and therefore suggests a means for generating and maintaining staircases.
Instability of flux-gradient laws
This mechanism is based on negative density diffusion as well. However, instead of combining temperature and salinity into a single density term, it treats both density components individually. In a publication by Radko, it is shown that formation of steps in numerical models is caused by the parametric variation of the flux ratio as a function of the density ratio , leading to an instability of equilibrium with uniform stratification. These unstable perturbations continuously grow in time until well-defined layers are formed.
Observations

Two types of staircases exist: salt-fingering staircases, where both temperature and salinity of the mixed layers decrease with pressure (and therefore with depth); and diffusive staircases, where both temperature and salinity of the mixed layers increase with pressure (so with depth).
Salt-fingering staircases
Most observations of salt-fingering staircases have come from three locations: the western Tropical Atlantic, the Tyrrhenian Sea, and the Mediterranean outflow. In these regions the density ratio has a very low value, which appears to be a condition for sufficient staircase formation. No staircases have been reported for values below 2. For values below 1.7, the step-like structures in vertical temperature and salinity profiles becomes apparent. Moreover, the spatial pattern of staircases is very sensitive to . With decreasing , the height of steps sharply increases and the staircases become more pronounced. The importance of the density ratio for the formation is a sign that staircases are a product of double diffusive convection.
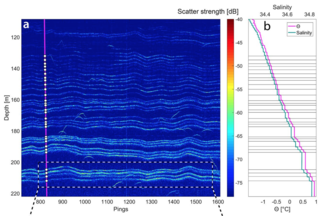
In the Tyrrhenian Sea, thermohaline staircases due to salt fingers are observed. The step-like shape is visible in the vertical temperature and salinity profiles. Staircases in the Tyrrhenian Sea show a very high stability in space and time. The weak deep circulation in this area might be an explanation for this stability.
Diffusive staircases
Diffusive staircases are found at higher latitudes. In the Arctic Ocean, warm and salty water from the Atlantic enters the Arctic basin and subducts beneath the colder and fresher waters of the upper Arctic. In some regions, also Pacific waters sit below the mixed layer and above the Atlantic layer. A thermocline is found at the top of the Atlantic Water layer. In that region, temperature and salinity increases with depth and step-like patterns are observed in vertical temperature and salinity profiles. These staircases mediate the heat transport from the warm water of Atlantic origin to the Arctic halocline and therefore serve as an important process in determining the heat flux from the Atlantic Water upward to the sea ice. Staircases in the Arctic are characterised by much smaller steps than in salt-fingering staircases.
On a much smaller scale, diffusive staircases have also been observed in low- and mid-latitudes. For example, Lake Kivu and Lake Nyos show characteristic staircase patterns. In these salt-water lakes, geothermal springs supply heat at the bottom resulting in the diffusive background stratification.
See also
References
- ^ Merryfield, William J. (2000-05-01). "Origin of Thermohaline Staircases". Journal of Physical Oceanography. 30 (5): 1046–1068. Bibcode:2000JPO....30.1046M. doi:10.1175/1520-0485(2000)030<1046:OOTS>2.0.CO;2. ISSN 0022-3670.
- ^ Radko, T.; Bulters, A.; Flanagan, J. D.; Campin, J.-M. (2014-05-01). "Double-Diffusive Recipes. Part I: Large-Scale Dynamics of Thermohaline Staircases". Journal of Physical Oceanography. 44 (5): 1269–1284. Bibcode:2014JPO....44.1269R. doi:10.1175/JPO-D-13-0155.1. hdl:1721.1/91958. ISSN 0022-3670. S2CID 66801727.
- ^ van der Boog, Carine G.; Koetsier, J. Otto; Dijkstra, Henk A.; Pietrzak, Julie D.; Katsman, Caroline A. (2021-01-13). "Global dataset of thermohaline staircases obtained from Argo floats and Ice-Tethered Profilers". Earth System Science Data. 13 (1): 43–61. Bibcode:2021ESSD...13...43V. doi:10.5194/essd-13-43-2021. ISSN 1866-3508. S2CID 234356971.
 Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
- ^ Radko, Timour (2013). Double-Diffusive Convection. Cambridge: Cambridge University Press. doi:10.1017/cbo9781139034173. ISBN 978-0-521-88074-9. S2CID 67802029.
- ^ Stern, Melvin E.; Stewart Turner, J. (1969-11-01). "Salt fingers and convecting layers". Deep Sea Research and Oceanographic Abstracts. 16 (5): 497–511. Bibcode:1969DSRA...16..497S. doi:10.1016/0011-7471(69)90038-2. ISSN 0011-7471.
- Stern, Melvin E. (January 1969). "Collective instability of salt fingers". Journal of Fluid Mechanics. 35 (2): 209–218. Bibcode:1969JFM....35..209S. doi:10.1017/S0022112069001066. ISSN 1469-7645. S2CID 121945515.
- Turner, J. S.; Stommel, Henry (1964-07-01). "A New Case of Convection in the Presence of Combined Vertical Salinity and Temperature Gradients". Proceedings of the National Academy of Sciences. 52 (1): 49–53. Bibcode:1964PNAS...52...49T. doi:10.1073/pnas.52.1.49. ISSN 0027-8424. PMC 300570. PMID 16591193.
- Huppert, Herbert E.; Linden, P. F. (December 1979). "On heating a stable salinity gradient from below". Journal of Fluid Mechanics. 95 (3): 431–464. Bibcode:1979JFM....95..431H. doi:10.1017/S0022112079001543. ISSN 1469-7645. S2CID 123813620.
- Radko, Timour (2003-12-25). "A mechanism for layer formation in a double-diffusive fluid". Journal of Fluid Mechanics. 497: 365–380. Bibcode:2003JFM...497..365R. doi:10.1017/S0022112003006785. S2CID 119737327.
- ^ Durante, S.; Schroeder, K.; Mazzei, L.; Pierini, S.; Borghini, M.; Sparnocchia, S. (2019). "Permanent Thermohaline Staircases in the Tyrrhenian Sea". Geophysical Research Letters. 46 (3): 1562–1570. Bibcode:2019GeoRL..46.1562D. doi:10.1029/2018GL081747. ISSN 1944-8007. S2CID 134607170.
- ^ Stranne, Christian; Mayer, Larry; Weber, Thomas C.; Ruddick, Barry R.; Jakobsson, Martin; Jerram, Kevin; Weidner, Elizabeth; Nilsson, Johan; Gårdfeldt, Katarina (2017-11-09). "Acoustic Mapping of Thermohaline Staircases in the Arctic Ocean". Scientific Reports. 7 (1): 15192. Bibcode:2017NatSR...715192S. doi:10.1038/s41598-017-15486-3. ISSN 2045-2322. PMC 5680214. PMID 29123176.
- Tait, R.I.; Howe, M.R. (1968-06-01). "Some observations of thermo-haline stratification in the deep ocean". Deep Sea Research and Oceanographic Abstracts. 15 (3): 275–280. Bibcode:1968DSRA...15..275T. doi:10.1016/0011-7471(68)90005-3. ISSN 0011-7471.
- Brown, Justin M.; Radko, Timour (2021-06-01). "Diffusive Staircases in Shear: Dynamics and Heat Transport". Journal of Physical Oceanography. 51 (6): 1915–1928. Bibcode:2021JPO....51.1915B. doi:10.1175/JPO-D-20-0193.1. ISSN 0022-3670. S2CID 233632601.
- Newman, Fred C. (1976-03-01). "Temperature Steps in Lake Kivu: A Bottom Heated Saline Lake". Journal of Physical Oceanography. 6 (2): 157–163. Bibcode:1976JPO.....6..157N. doi:10.1175/1520-0485(1976)006<0157:TSILKA>2.0.CO;2. ISSN 0022-3670.
- Schmid, Martin; Lorke, Andreas; Dinkel, Christian; Tanyileke, Gregory; Wüest, Alfred (August 2004). "Double-diffusive convection in Lake Nyos, Cameroon". Deep Sea Research Part I: Oceanographic Research Papers. 51 (8): 1097–1111. Bibcode:2004DSRI...51.1097S. doi:10.1016/j.dsr.2004.02.010.
 and
and  . Here,
. Here,  , and
, and  represent the conservative temperature, salinity, and density variations in the mixed layer.
represent the conservative temperature, salinity, and density variations in the mixed layer.  and
and  represent the conservative temperature, salinity, and density variations in the interface.
represent the conservative temperature, salinity, and density variations in the interface.  , and
, and  denote the height of the mixed layer and of the interface respectively.
denote the height of the mixed layer and of the interface respectively.  represent the averages of conservative temperature, salinity and pressure in the mixed layer.
represent the averages of conservative temperature, salinity and pressure in the mixed layer. , with
, with  the pressure and
the pressure and 
 the reference pressure. The vertical conservative temperature, absolute salinity, and potential density gradients are all below the threshold value by meeting these three conditions:
the reference pressure. The vertical conservative temperature, absolute salinity, and potential density gradients are all below the threshold value by meeting these three conditions:



 the
the  the
the  the reference density,
the reference density,  the conservative temperature, and
the conservative temperature, and  the salinity.
the salinity.
 should be larger than the variations within each mixed layer
should be larger than the variations within each mixed layer  to ensure a stepped structure. Therefore the following conditions should be met:
to ensure a stepped structure. Therefore the following conditions should be met:



 . The interface height should be smaller than the height of the mixed layers directly above and below the interface
. The interface height should be smaller than the height of the mixed layers directly above and below the interface  . This condition has to be met in order to ensure that the interface is relatively thin compared to the mixed layers surrounding it. Furthermore, the algorithm removes all interfaces with conservative temperature or absolute salinity inversions to make sure that it only detects step-like structures that are associated with the presence of thermohaline staircases.
. This condition has to be met in order to ensure that the interface is relatively thin compared to the mixed layers surrounding it. Furthermore, the algorithm removes all interfaces with conservative temperature or absolute salinity inversions to make sure that it only detects step-like structures that are associated with the presence of thermohaline staircases.
 and interfaces with diffusive-convective characteristics should correspond to Turner angles of
and interfaces with diffusive-convective characteristics should correspond to Turner angles of  .
.
 . This proposition relies on the presence of lateral property gradients to drive interleaving. This mechanism, where thermohaline intrusions are transformed into staircases, are likely to exist in strong temperature-salinity fronts.
. This proposition relies on the presence of lateral property gradients to drive interleaving. This mechanism, where thermohaline intrusions are transformed into staircases, are likely to exist in strong temperature-salinity fronts.
 values below 2. For values below 1.7, the step-like structures in vertical temperature and salinity profiles becomes apparent. Moreover, the spatial pattern of staircases is very sensitive to
values below 2. For values below 1.7, the step-like structures in vertical temperature and salinity profiles becomes apparent. Moreover, the spatial pattern of staircases is very sensitive to  and salinity profiles with black horizontal lines indicating the depth of the individual layers identified in the echogram.
and salinity profiles with black horizontal lines indicating the depth of the individual layers identified in the echogram.