| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (June 2014) (Learn how and when to remove this message) |
In physics, the total position-spread (TPS) tensor is a quantity originally introduced in the modern theory of electrical conductivity. In the case of molecular systems, this tensor measures the fluctuation of the electrons around their mean positions, which corresponds to the delocalization of the electronic charge within a molecular system. The total position-spread can discriminate between metals and insulators taking information from the ground state wave function. This quantity can be very useful as an indicator to characterize Intervalence charge transfer processes, the bond nature of molecules (covalent, ionic, or weakly bonded), and Metal–insulator transition.
Overview
The Localization Tensor (LT) is a per electron quantity proposed in the context of the theory of Kohn to characterize electrical conductivity properties. In 1964, Kohn realized that electrical conductivity is more related to the proper delocalization of the wave function than a simple bandgap. In fact, he proposed that a qualitative difference between insulators and conductors also manifests as a different organization of the electrons in their ground state where one has that: the wave function is strongly localized in insulators and very delocalized in conductors.
The interesting outcome of this theory is: i) it relates the classical idea of localized electrons as a cause of insulating state; ii) the needed information can be recovered from the ground state wave function because in the insulated regime the wave function breaks down as a sum of disconnected terms.
It is until 1999 that Resta and coworkers found a way to define the Kohn delocalization by proposing the already mentioned Localization Tensor. The LT is defined as a second order moment cumulant of the position operator divided by the number of electrons in the system. The key property of the LT is that: it diverges for metals while it takes finite values for insulators in the Thermodynamic limit.
Recently, the global quantity (the LT not divided by the number of electrons) has been introduced to study molecules and named Total Position-Spread tensor.
Theory
Spin-summed total position-spread (SS-TPS)
The total position spread Λ is defined as the second moment cumulant of the total electron position operator, and its units are in length square (e.g. bohr²). In order to compute this quantity, one has to take into account the position operator and its tensorial square. For a system of n electrons, the position operator and its Cartesian components are defined as: (total position)
Where the i index runs over the number of electrons. Each component of the position operator is a one-electron operator, they can be represented in second quantization as follows: where i,j run over orbitals. The expectation values of the position components are the first moments of the electrons' position.
Now we consider the tensorial square (second moment). In this sense, there are two types of them:
- in quantum chemistry programs like MOLPRO or DALTON the second moment operator is a tensor defined as the sum of the tensor squares of the positions of a single electron. Then, this is a one-electron operator s defined by its Cartesian components: where index i runs over the number of electrons.
- there is also the square of the total position operator . This is a two-electron operator S, and also defined by its Cartesian components: where indices i,j run over electrons.
The second moment of the position becomes then the sum of the one- and two-electron operators already defined:
Given a n-electron wave function , one wants to compute the second moment cumulant of it. A cumulant is a linear combination of moments so we have:
Spin-partitioned total position-spread (SP-TPS)
The position operator can be partitioned according to spin components.
From the one-particle operator it is possible to define the total spin-partitioned position operator as:
Therefore, the total position operator can be expressed by the sum of the two spin parts and :
and the square of the total position operator decomposes as:
Thus, there are four joint second moment cumulant of the spin-partitioned position operator:
Applications
Model Hamiltonians
Hubbard model

The Hubbard model is a very simple and approximate model employed in Condensed matter physics to describe the transition of materials from metals to insulators. It takes into account only two parameters: i) the kinetic energy or hopping integral denoted by -t; and ii) the on-site repulsion between electrons represented by U (see the example of 1D chain of hydrogen atoms).
In Figure 1, there are two limit cases to consider: larger values of -t/U representing a strong charge fluctuation (electrons free to move) whereas for small values of -t/U the electrons are completely localized. The spin-summed total position-spread is very sensitive to these changes because it increases faster than linearly when electrons start to present mobility (0.0 to 0.5 range of -t/U).
Heisenberg model
Monitor the wave function

The total position-spread is a powerful tool to monitor the wave function. In Figure 3 is shown the longitudinal spin-summed total position-spread (Λ) computed at full configuration interaction level for the H2 diatomic molecule. The Λ in the high repulsive region shows a value that is lower than in the asymptotic limit. This is a consequence of nuclei being near to each other's causing and enhancement of the effective nuclear charge that makes electrons to be more localized. When stretching the bond, the total position-spread starts growing until it reaches a maximum (strong delocalization of the wave function) before the bond is broken. Once the bond is broken, the wave function becomes a sum of disconnected localized regions, and the tensor decreases until it reaches twice the value of the atomic limit (1 bohr² for each hydrogen atom).
Spin delocalization
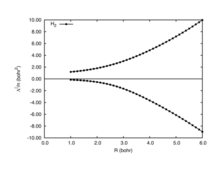
When the total position-spread tensor is partitioned according to spin (spin-partitioned total position-spread), it becomes a powerful tool to describe spin delocalization in the insulating regime. In Figure 4 is shown the longitudinal spin-partitioned total position-spread (Λ) computed at full configuration interaction level for the H2 diatomic molecule. The horizontal line at 0 bohr divides the same spin (positive values) and different spin (negative values) contributions of the spin partitioned total position-spread. Unlike the spin-summed total position-spread that saturates to the atomic value for R>5, the spin-partitioned total position-spread diverges as R indicating that there is a strong spin delocalization. The spin-partitioned total position-spread can also be seen as a measure of how strong the electron correlation is.
Properties
The total position-spread is a cumulant and thus it possesses the following properties:
- Cumulants can be explicitly represented only by moments of lower or equal order.
- Cumulants are a linear combination of the products of these moments of lower or equal order.
- Cumulants are additive. This is a very important property when studying molecular systems because it means that the total position-spread tensor shows size consistency.
- A diagonal element of the cumulant tensor is the variance (see also this article), and it is always a positive value.
- Cumulants also are invariant under the translation of the origin of when they are of order ≥ 2. The total position-spread tensor being a second-order cumulant, is invariant under the translation of the origin.
- The total position-spread is more sensitive to the variation of the wave function than the energy, which makes it a good indicator for instance in a Metal–insulator transition situation.
References
- W. Kohn (1964). "Theory of the Insulating State". Phys. Rev. 133 (1A): A171 – A181. Bibcode:1964PhRv..133..171K. doi:10.1103/PhysRev.133.A171.
- R. Resta; S. Sorella (1999). "Electron Localization in the Insulating State". Phys. Rev. Lett. 82 (2): 370. arXiv:cond-mat/9808151. Bibcode:1999PhRvL..82..370R. doi:10.1103/PhysRevLett.82.370. S2CID 118962750.
- O. Brea; M. El Khatib; C. Angeli; G.L. Bendazzoli; S. Evangelisti; T. Leininger (2013). "Behavior of the Position–Spread Tensor in Diatomic Systems". J. Chem. Theory Comput. 9 (12): 5286–5295. doi:10.1021/ct400453b. PMID 26592266.
- M. El Khatib; T. Leininger; G. L. Bendazzoli; S. Evangelisti (2014). "Computing the Position-Spread Tensor in the CAS-SCF formalism". Chem. Phys. Lett. 591 (2): 58. Bibcode:2014CPL...591...58E. doi:10.1016/j.cplett.2013.10.080.
- R. Kubo (1962). "Generalized cumulant expansion method". Journal of the Physical Society of Japan. 17 (7): 1100–1120. Bibcode:1962JPSJ...17.1100K. doi:10.1143/JPSJ.17.1100.
 (total position)
(total position)

 where i,j run over orbitals. The expectation values of the position components are the first moments of the electrons' position.
where i,j run over orbitals. The expectation values of the position components are the first moments of the electrons' position.
 where index i runs over the number of electrons.
where index i runs over the number of electrons. . This is a two-electron operator S, and also defined by its Cartesian components:
. This is a two-electron operator S, and also defined by its Cartesian components:  where indices i,j run over electrons.
where indices i,j run over electrons.
 , one wants to compute the second moment cumulant of it. A cumulant is a linear combination of moments so we have:
, one wants to compute the second moment cumulant of it. A cumulant is a linear combination of moments so we have:



 can be expressed by the sum of the two spin parts
can be expressed by the sum of the two spin parts  and
and  :
:


