| This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources. Find sources: "Tukey depth" – news · newspapers · books · scholar · JSTOR (May 2024) |
In statistics and computational geometry, the Tukey depth is a measure of the depth of a point in a fixed set of points. The concept is named after its inventor, John Tukey. Given a set of n points in d-dimensional space, Tukey's depth of a point x is the smallest fraction (or number) of points in any closed halfspace that contains x.
Tukey's depth measures how extreme a point is with respect to a point cloud. It is used to define the bagplot, a bivariate generalization of the boxplot.
For example, for any extreme point of the convex hull there is always a (closed) halfspace that contains only that point, and hence its Tukey depth as a fraction is 1/n.
Definitions
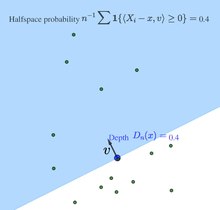
Sample Tukey's depth of point x, or Tukey's depth of x with respect to the point cloud , is defined as
where is the indicator function that equals 1 if its argument holds true or 0 otherwise.
Population Tukey's depth of x wrt to a distribution is
where X is a random variable following distribution .
Tukey mean and relation to centerpoint
A centerpoint c of a point set of size n is nothing else but a point of Tukey depth of at least n/(d + 1).
See also
References
- Tukey, John W (1975). Mathematics and the Picturing of Data. Proceedings of the International Congress of Mathematicians. p. 523-531.
This mathematics-related article is a stub. You can help Misplaced Pages by expanding it. |
 in d-dimensional space, Tukey's depth of a point x is the smallest fraction (or number) of points in any closed
in d-dimensional space, Tukey's depth of a point x is the smallest fraction (or number) of points in any closed  , is defined as
, is defined as

 is the
is the  is
is
