This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

- The article considers only curves in Euclidean space. More General information about curves can be found in the same article about rimanov pseudonymo and diversity. Questions regarding curves in an arbitrary topological space, see the main article devoted to curves.
Differential geometry curves — section of geometry that deals with smooth curves in the plane and in Euclidean space and uses for this the methods of integral and differential calculus.
Since ancient times, different curves were analyzed using synthetic methods. Differential geometry works differently: the curves presented in parameterized form, and their geometric properties and characteristics associated with them such as curvature and curve length, are expressed via derivatives and integrals using vector calculus. One of the most important means of analysis of the curve is the Freinet frame — movable frame, which provides the "best" coordinate system at each point of the curve.
The theory curves are much smaller and simpler than the differential geometry of surfaces and its multidimensional generalizations, because a regular curve in Euclidean space has no intrinsic geometry. Any smooth curve can be parameterized by arc length (the natural parametrization) and from the point of view of the insect which is crawling along the curve and knows nothing about our surroundings, all her curves will seem the same. The various curves in space differ in the way they bend. Quantitatively it is measured by the differential-geometric nvariant called Krivine and torsion. The main theorem of the theory of curves argues that the knowledge of these invariants completely determines the curve.
Definition
Let n be a natural number, r a natural number or ∞, I denotes a non-empty interval on the number line and I. t belongs to the Vector-valued function
class C (i.e. γ is r times continuously dfferential) is called a parametric curve of class C or C-parametrizes curve γ. t is called the parameter of the curve γ. γ(I) is called the image of the curve. It is important to distinguish between a curve γ and the image curve γ(I), because the image curve can be described by several different curves various classes C.
We can assume that the parameter t represents time, and the curve γ(t) is the trajectory of an object moving in space.
If I is a closed interval , the point γ(a) is called the initial point and γ(b) is the endpoint of the curve γ.
If γ(a) = γ(b) say that a closed curve or loop. In addition, they say that γ a closed Cr-curve if γ(k)(a) = γ(k)(b) for all k ≤ r.
If γ:(a,b) →R — n ctive mapping, then we say that the curve is simple.
If parametrically defined curve γ can be locally described as a power series, then we say that the curve analytic or of class .
Write γ to denote that the curve is traversed in the opposite direction.
C-curve be smooth of order m, if for each t of the interval I
— linearly independent vectors in R.
In particular,C- the curve γ is smooth if for each .
Parapanamerican and the equivalence relation
The way of curve can correspond to several different parameterizations of the curve. Goal differential geometry to describe the invariants of the curves is independent of the different parameterizations. Therefore, you need to define an equivalence relation on the set of all parameterized curves. The properties of the differential geometry of the curve (length, rapper Freinet and generalized curvature) is relatively nvariant parapanamerican and therefore are properties of equivalence classes. Equivalence classes are called C-curves and are Central objects of study in differential geometry of curves.
Two parametric curves of class C
and
say, are equivalent if there exists a bijective C-smooth display
such that
and
γ2 call parapanamerican γ1.This parapanamerican γ1 defines an equivalence relation on the set of all C-curves. The equivalence class is called C- curve.
You can define even finer equivalence relation of oriented to C-кривих,if require to φ it was φ‘(t) > 0.
Equivalent C-the curves have the same images curves. And equivalent oriented C-curves are traversed in the same direction.
Length and natural parametrization
The length l of a curve γ : → R class C can be defined as follows:
The length of the curve is invariant under parapanamerican curve and therefore is a property of the curve, which is discussed in differential geometry.
For each smooth C-curve (r at least 1) γ: → R you can define a function
Recording
where t(s) is the inverse function to s(t), we obtain parapanamerican the curve γ is called a natural or natural. They say that the curve is parameterized by arc length, or it is set to parameterization of the single speed. The parameter s(t) is called the natural parameter of γ.
This parameterization is convenient because the natural parameter s(t) runs over the image of γ with unit speed, that is
Usually in practice it is difficult to obtain a natural parameterization of the curve, however, in theoretical reasoning, it is convenient to consider curves given natural parametricity.
For a given curve γ(t) is unique up selection direction of traversal of the curve.
Size
often called the energy or action of the curve; this name is justified by the fact that the equation of the geodesic line equation is the Euler-Lagrange motion for such action.
Touch curves
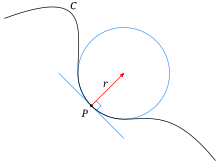
The two curves , have a common point touch of order n, if they have the same derivatives only up to n-th order:
For example, the tangent line is a line which is tangent of the curve is not lower than 1-th order. Among the circles tangential to the curve secrete stione circle, which is tangent of the curve, not below 2-nd order.
The curvature of the curve

The curvature of the curve determines a quantitative measure of the deviation of the curve from the tangent line. Following are the geometric definition of curvature C-the smooth curve.
Let the point P belongs to the regular curve γ, a point Q on the curve near the point P. we denote by the angle between the tangents at the points P and Q, and using the arc length of the curve between points P and Q. Then criminal the curve γ at the point P is called the limit
It is obvious that if the curve γ was a straight line, the tangents to them would coincide with the straight line and, therefore, the angle will be zero, and hence the curvature of a straight is zero. Using the above definition it is easy to calculate Krivine of a circle of radius R, it is equal to .Therefore, the magnitude inverse to the curvature is called the radius of curvature.
Sometimes Kevin ascribe sign. If the curvature can be negative, it is referred to as , when does the module curvature, referred to as
The calculation of the curvature of a plane curve
Let the curve set to the radius vector
To calculate the curvature of a plane curve using the formula (the derivative is taken on the parameter t):
Without the use of coordinates ( — the cross product):
Computation of curvature of a curve in space
Let the curve set to the radius vector Krivine curve can be found by the formula:
Without the use of coordinates:
Equivalent formula:
Here t denotes the transpose of a matrix. The last formula can be used to calculate the curvature of a curve in Euclidean space of arbitrary dimension.
Notes
References
- Борисенко, О. А. . ISBN 5-7768-0388-8.
{{cite book}}: Missing or empty|title=(help) - Погорєлов О. В. . ISBN 5-93972-068-4.
{{cite book}}: Missing or empty|title=(help)

 .
.
 be smooth of order m, if for each t of the interval I
be smooth of order m, if for each t of the interval I

 for each
for each  .
.








 the curve γ is called a natural or natural. They say that the curve is parameterized by arc length, or it is set to parameterization of the single speed. The parameter s(t) is called the natural parameter of γ.
the curve γ is called a natural or natural. They say that the curve is parameterized by arc length, or it is set to parameterization of the single speed. The parameter s(t) is called the natural parameter of γ.


 ,
,  have a common point
have a common point  touch of order n, if they have the same derivatives only up to n-th order:
touch of order n, if they have the same derivatives only up to n-th order:

 the angle between the tangents at the points P and Q, and using
the angle between the tangents at the points P and Q, and using  the arc length of the curve between points P and Q. Then criminal the curve γ at the point P is called the limit
the arc length of the curve between points P and Q. Then criminal the curve γ at the point P is called the limit 
 .Therefore, the magnitude inverse to the curvature is called the radius of curvature.
.Therefore, the magnitude inverse to the curvature is called the radius of curvature.
 , when does the module curvature, referred to as
, when does the module curvature, referred to as 


 — the cross product):
— the cross product):

 Krivine curve can be found by the formula:
Krivine curve can be found by the formula:


