


A vertical-axis wind turbine (VAWT) is a type of wind turbine where the main rotor shaft is set transverse to the wind while the main components are located at the base of the turbine. This arrangement allows the generator and gearbox to be located close to the ground, facilitating service and repair. VAWTs do not need to be pointed into the wind, which removes the need for wind-sensing and orientation mechanisms. Major drawbacks for the early designs (Savonius, Darrieus and giromill) included the significant torque ripple during each revolution and the large bending moments on the blades. Later designs addressed the torque ripple by sweeping the blades helically (Gorlov type). Savonius vertical-axis wind turbines (VAWT) are not widespread, but their simplicity and better performance in disturbed flow-fields, compared to small horizontal-axis wind turbines (HAWT) make them a good alternative for distributed generation devices in an urban environment.
A vertical axis wind turbine has its axis perpendicular to the wind streamlines and vertical to the ground. A more general term that includes this option is a "transverse axis wind turbine" or "cross-flow wind turbine". For example, the original Darrieus patent, US patent 1835018, includes both options.
Drag-type VAWTs such as the Savonius rotor typically operate at lower tip speed ratios than lift-based VAWTs such as Darrieus rotors and cycloturbines.
Computer modelling suggests that vertical-axis wind turbines arranged in wind farms may generate more than 15% more power per turbine than when acting in isolation.
General aerodynamics
The forces and the velocities acting in a Darrieus turbine are depicted in Figure 1. The resultant velocity vector, , is the vectorial sum of the undisturbed upstream air velocity, , and the velocity vector of the advancing blade, .
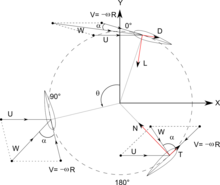
Thus the oncoming fluid velocity varies during each cycle. Maximum velocity is found for and the minimum is found for , where is the azimuthal or orbital blade position. The angle of attack, , is the angle between the oncoming air speed, W, and the blade's chord. The resultant airflow creates a varying, positive angle of attack to the blade in the upstream zone of the machine, switching sign in the downstream zone of the machine.
It follows from geometric considerations of angular velocity as seen in the accompanying figure that:
and:
Solving for the relative velocity as the resultant of the tangential and normal components yields:
Thus, combining the above with the definitions for the tip speed ratio yields the following expression for the resultant velocity:
Angle of attack is solved as:
Which when substituting the above yields:
The resultant aerodynamic force is resolved either into lift (L) - drag (D) components or normal (N) - tangential (T) components. The forces are considered to be acting at the quarter-chord point, and the pitching moment is determined to resolve the aerodynamic forces. The aeronautical terms lift and drag refer to the forces across (lift) and along (drag) the approaching net relative airflow. The tangential force acts along the blade's velocity, pulling the blade around, and the normal force acts radially, pushing against the shaft bearings. The lift and the drag force are useful when dealing with the aerodynamic forces around the blade such as dynamic stall, boundary layer etc.; while when dealing with global performance, fatigue loads, etc., it is more convenient to have a normal-tangential frame. The lift and the drag coefficients are usually normalised by the dynamic pressure of the relative airflow, while the dynamic pressure of undisturbed upstream fluid velocity usually normalises the normal and tangential coefficients.
A = Blade Area (not to be confused with the Swept Area, which is equal to the height of the blade/rotor times the rotor diameter), R = Radius of turbine
The amount of power, P, that can be absorbed by a wind turbine:
Where is the power coefficient, is air density, is the swept area of the turbine, and is the wind speed.
Types
There are two main types of Vertical Axis Wind Turbines. I.e. Savonius Wind turbine and Darrieus wind turbine. The Darrieus rotor comes in various subforms, including helix-shaped, disc-like, and the H-rotor with straight blades. These turbines typically have three slim rotor blades driven by lift forces, allowing them to achieve high speeds.
Various simple designs may exist for vertical wind turbines, as detailed below. In practice, you may come across a range of variations and combinations, with developers frequently demonstrating their creativity in crafting diverse forms of vertical wind turbines.

Savonius

The Savonius wind turbine (SWT) is a drag-type VAWT. The common design includes a rotating shaft with two or three scoops that catch the incoming wind. Due to its simplistic and robust design and its relatively low efficiency it is used whenever reliability is more important than efficiency. One reason for the low efficiency of a Savonius wind turbine is that roughly only half of the turbine generates positive torque, while the other side moves against the wind and thus produces negative torque. A variant of SWT is the Harmony wind turbine with helix-shaped blades and an automatic furling mechanism during high-speed wind conditions.
Darrieus
The Darrieus wind turbine is a lift-type VAWT. The original design included a number of curved aerofoil blades with the tips attached on a rotating shaft. However, there are also designs that use straight vertical airfoils, referred to as H-rotor or Giromill Darrieus wind turbines. Furthermore, the blades of the Darrieus wind turbine can be shaped into a helix to reduce the torque ripple effect on the turbine by spreading the torque evenly over the revolution.
Being lift-type devices, the Darrieus wind turbines can extract more power from the wind than drag-type wind turbines, such as the Savonius wind turbine.
Revolving wing
Revolving wing wind turbines or rotating wing wind turbines are a new category of lift-type VAWTs which use 1 vertically standing, non-helical airfoil to generate 360-degree rotation around a vertical shaft that runs through the center of the airfoil.
Advantages
VAWTs offer a number of advantages over traditional horizontal-axis wind turbines (HAWTs):
- Omni-directional VAWTs may not need to track the wind. This means they don't require a complex mechanism and motors to yaw the rotor and pitch the blades.
- Gearbox replacement and maintenance are simpler and more efficient, because the gearbox is accessible at ground level instead of requiring the operator work hundreds of feet in the air. Motor and gearbox failures generally are significant operation and maintenance considerations.
- Some designs can use screw pile foundations, which reduces the road transport of concrete and the environmental impact of installation. Screw piles can be fully recycled at end of life.
- VAWTs can be installed on HAWT wind farms below the existing HAWTs, supplementing power output.
- VAWTs may operate in conditions unsuitable for HAWTs. For example, the Savonius rotor, which can operate in irregular, slow wind ground-level contexts, is often used in remote or unattended locations although it is the most 'inefficient', drag-type, VAWT.
- Reduced noise compared to HAWTs
- Reduced danger for birds
Disadvantages
When the velocity of a VAWT wind turbine grows, so does the power, however at a certain peak point, the power progressively decreases to zero even while the wind turbine velocity is at its greatest. Such that, disc brakes are used to slow the velocity of a wind turbine at high wind conditions. However, sometimes due to disc brake overheating, the turbine can catch fire.
VAWTs often suffer from dynamic stall of the blades as the angle of attack varies rapidly.
The blades of a VAWT are fatigue-prone due to the wide variation in applied forces during each rotation. The vertically oriented blades can twist and bend during each turn, shortening their usable lifetimes.
Other than the drag-types, VAWTs have proven less reliable than HAWTs, although modern designs have overcome many early issues.
Research
A 2021 study simulated a VAWT configuration that allowed VAWTs to beat a comparable HAWT installation by 15%. An 11,500-hour simulation demonstrated the increased efficiency, in part by using a grid formation. One effect is to avoid downstream turbulence stemming from grid-arranged HAWTs that lowers efficiency. Other optimizations included array angle, rotation direction, turbine spacing, and number of rotors.
In 2022 Norway's World Wide Wind introduced floating VAWTs with two sets of counter-rotating blades. The two sets are fixed to concentric shafts. Each has an attached turbine. One is attached to the rotor, the other to the stator. This has the effect of doubling their speed relative to each other versus a static stator. They claimed to more than double the output compared to the largest HAWTs. HAWTs require heavy drivetrains, gearboxes, generators and blades at the top of the tower, necessitating heavy underwater counterbalances. VAWTs place most of the heavy components at the bottom of the tower, reducing the need for counterbalance. The blades sweep a conical area, which helps reduce the turbulence downwind of each tower, increasing the maximum tower density. The company claims it will build a 400 m (1,300 ft) 40-megawatt unit.
Applications

The Windspire, a small VAWT intended for individual (home or office) use was developed in the early 2000s by US company Mariah Power. The company reported that several units had been installed across the US by June 2008.
Arborwind, an Ann Arbor, Michigan, based company, produces a patented small VAWT which has been installed at several US locations as of 2013.
In 2011, Sandia National Laboratories wind-energy researchers began a five-year study of applying VAWT design technology to offshore wind farms. The researchers stated: "The economics of offshore windpower are different from land-based turbines, due to installation and operational challenges. VAWTs offer three big advantages that could reduce the cost of wind energy: a lower turbine center of gravity; reduced machine complexity; and better scalability to very large sizes. A lower center of gravity means improved stability afloat and lower gravitational fatigue loads. Additionally, the drivetrain on a VAWT is at or near the surface, potentially making maintenance easier and less time-consuming. Fewer parts, lower fatigue loads and simpler maintenance all lead to reduced maintenance costs."
A 24-unit VAWT demonstration plot was installed in southern California in the early 2010s by Caltech aeronautical professor John Dabiri. His design was incorporated in a 10-unit generating farm installed in 2013 in the Alaskan village of Igiugig.
Dulas, Anglesey, received permission in March 2014 to install a prototype VAWT on the breakwater at Port Talbot waterside. The turbine is a new design, supplied by Wales-based C-FEC (Swansea), and will be operated for a two-year trial. This VAWT incorporates a wind shield which blocks the wind from the advancing blades, and thus requires a wind-direction sensor and a positioning mechanism, as opposed to the "egg-beater" types of VAWTs discussed above.
StrongWind, a Canadian based company produces a patented urban VAWT which has been installed in several Canadian and international locations as of 2023.
Architect Michael Reynolds (known for his Earthship house designs) developed a 4th-generation VAWT named Dynasphere. It has two 1.5 kW generators and can produce electricity at very low speeds.
See also
References
- Jha, A. R. (2010). Wind turbine technology. Boca Raton, Florida, USA: CRC Press.
- Raciti Castelli, Marco; Englaro, Alessandro; Benini, Ernesto (2011). "The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD". Energy. 36 (8): 4919–4934. Bibcode:2011Ene....36.4919R. doi:10.1016/j.energy.2011.05.036.
- Battisti, L.; Brighenti, A.; Benini, E.; Castelli, M. Raciti (September 2016). "Analysis of Different Blade Architectures on small VAWT Performance". Journal of Physics: Conference Series. 753 (6): 062009. Bibcode:2016JPhCS.753f2009B. doi:10.1088/1742-6596/753/6/062009. hdl:11572/152690. S2CID 4880064.
- Longo, Riccardo; Nicastro, Patricia; Natalini, Matteo; Schito, Paolo; Mereu, Riccardo; Parente, Alessandro (August 2020). "Impact of urban environment on Savonius wind turbine performance: A numerical perspective" (PDF). Renewable Energy. 156: 407–422. Bibcode:2020REne..156..407L. doi:10.1016/j.renene.2020.03.101. hdl:11311/1136273. S2CID 219003726.
- "Vertical turbines could be the future for wind farms". EurekAlert!.
- Hansen, Joachim Toftegaard; Mahak, Mahak; Tzanakis, Iakovos (June 2021). "Numerical modelling and optimization of vertical axis wind turbine pairs: A scale up approach". Renewable Energy. 171: 1371–1381. Bibcode:2021REne..171.1371H. doi:10.1016/j.renene.2021.03.001.
- Islam, M.; Ting, D.; Fartaj, A. (2008). "Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines". Renewable and Sustainable Energy Reviews. 12 (4): 1087–1109. Bibcode:2008RSERv..12.1087I. doi:10.1016/j.rser.2006.10.023.
- "Vertical Axis Wind Turbine development, Guilherme Silva" (PDF).
- El Kasmi, Amina; Masson, Christian (2008). "An extended k–ε model for turbulent flow through horizontal-axis wind turbines". Journal of Wind Engineering and Industrial Aerodynamics. 96: 103–122. doi:10.1016/j.jweia.2007.03.007.
- Eriksson, S.; Bernhoff, H.; Leijon, M. (2008). "Evaluation of different turbine concepts for wind power". Renewable and Sustainable Energy Reviews. 12 (5): 1419–1434. Bibcode:2008RSERv..12.1419E. doi:10.1016/j.rser.2006.05.017.
- "Harmony Turbines – ...we now have the power to change the world!". harmonyturbines.com. Retrieved 2022-10-20.
- Wicaksono, Yoga Arob; Tjahjana, Dominicus Danardono Dwi Prija; Hadi, Syamsul (2018). "Influence of omni-directional guide vane on the performance of cross-flow rotor for urban wind energy". The 3rd International Conference on Industrial. AIP Conference Proceedings. 1927 (1): 030040. Bibcode:2018AIPC.1931c0040W. doi:10.1063/1.5024099. ISSN 0094-243X.
- Peace, Steven (2004-06-01). "Another Approach to Wind". Mechanical Engineering. 126 (6): 28–31. doi:10.1115/1.2004-JUN-2.
- Erik Möllerström; Fredric Ottermo; Jonny Hylander; Hans Bernhoff (2016). "Noise Emission of a 200 kW Vertical Axis Wind Turbine" (PDF). Energies. 9: 19. doi:10.3390/en9010019. Retrieved 2022-09-15.
- "Bird-Safe Wind Turbines". 2018-09-12. Retrieved 2022-09-15.
- Anish Paudel; Mahato, Rahul; Devkota, Santosh; Sandip Paudel (August 2022). "DESIGN AND ANALYSIS OF HARMONY WIND TURBINE". doi:10.13140/RG.2.2.33181.38883.
{{cite journal}}: Cite journal requires|journal=(help) - Buchner, A.-J.; Soria, J.; Honnery, D.; Smits, A. J. (2018). "Dynamic stall in vertical axis wind turbines: Scaling and topological considerations". Journal of Fluid Mechanics. 841: 746–766. Bibcode:2018JFM...841..746B. doi:10.1017/jfm.2018.112. S2CID 126033643.
- Buchner, A.-J.; Lohry, M. W.; Martinelli, L.; Soria, J.; Smits, A. J. (2015). "Dynamic stall in vertical axis wind turbines: Comparing experiments and computations". Journal of Wind Engineering and Industrial Aerodynamics. 146: 163–171. Bibcode:2015JWEIA.146..163B. doi:10.1016/j.jweia.2015.09.001.
- Simão Ferreira, Carlos; Van Kuik, Gijs; Van Bussel, Gerard; Scarano, Fulvio (2008). "Visualization by PIV of dynamic stall on a vertical axis wind turbine". Experiments in Fluids. 46 (1): 97–108. Bibcode:2009ExFl...46...97S. doi:10.1007/s00348-008-0543-z.
- Chiras, Dan (2010). Wind Power Basics: A Green Energy Guide. New Society. p. 87. ISBN 978-0-86571-617-9.
- Ashwill, Thomas D.; Sutherland, Herbert J.; Berg, Dale E. (2012-01-01). A retrospective of VAWT technology (Report). doi:10.2172/1035336 – via University of North Texas Libraries, UNT Digital Library https://digital.library.unt.edu; UNT Libraries Government Documents Department.
{{cite report}}: External link in|via= - Kear, Matt; Evans, Ben; Ellis, Rob; Rolland, Sam (January 2016). "Computational aerodynamic optimisation of vertical axis wind turbine blades". Applied Mathematical Modelling. 40 (2): 1038–1051. doi:10.1016/j.apm.2015.07.001. ISSN 0307-904X.
- Koop, Fermin (2021-04-27). "The future of wind farms is vertical, striking new study claims". ZME Science. Retrieved 2021-04-29.
- Blain, Loz (2022-08-30). "Contra-rotating floating turbines promise unprecedented scale and power". New Atlas. Retrieved 2022-08-31.
- LaMonica, Martin (2008-06-02). "Vertical-axis wind turbine spins into business". CNET. Retrieved 2015-09-18.
- "History". Arbor Wind. Retrieved 2015-09-18.
- Holinka, Stephanie (2012-08-08). "Offshore Use of Vertical-axis Wind Turbines Gets Closer Look". Renewable Energy World. Retrieved 2015-09-18.
- Bullis, Kevin (2013-04-08). "Will Vertical Turbines Make More of the Wind?". MIT Technology Review. Retrieved 2015-09-18.
- ^ "C-FEC". Archived from the original on 2016-03-18. Retrieved 2024-09-02.
- "Dulas secures consent for prototype 'vertical axis' wind turbine". Renewable Energy Focus. 2014-03-05. Retrieved 2015-09-18.
- "strongwind.ca". strongwind.ca. Retrieved 2023-12-01.
- "Vertical Axis Wind Power Generation Prototype". Earthship Biotecture. Archived from the original on 2022-06-11. Retrieved 2015-09-18.
External links
- Cellar Image of the Day Shows a VAWT transverse to the wind, yet with the axis horizontal, but such does not allow the machine to be called a HAWT.
 , is the vectorial sum of the undisturbed upstream air velocity,
, is the vectorial sum of the undisturbed upstream air velocity,  , and the velocity vector of the advancing blade,
, and the velocity vector of the advancing blade,  .
.

 and the minimum is found for
and the minimum is found for  , where
, where  is the azimuthal or orbital blade position. The
is the azimuthal or orbital blade position. The  , is the angle between the oncoming air speed, W, and the blade's chord. The resultant airflow creates a varying, positive angle of attack to the blade in the upstream zone of the machine, switching sign in the downstream zone of the machine.
, is the angle between the oncoming air speed, W, and the blade's chord. The resultant airflow creates a varying, positive angle of attack to the blade in the upstream zone of the machine, switching sign in the downstream zone of the machine.



 yields the following expression for the resultant velocity:
yields the following expression for the resultant velocity:





 is the power coefficient,
is the power coefficient,  is air density,
is air density,  is the swept area of the turbine, and
is the swept area of the turbine, and  is the wind speed.
is the wind speed.