This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Visual information fidelity (VIF) is a full reference image quality assessment index based on natural scene statistics and the notion of image information extracted by the human visual system. It was developed by Hamid R Sheikh and Alan Bovik at the Laboratory for Image and Video Engineering (LIVE) at the University of Texas at Austin in 2006. It is deployed in the core of the Netflix VMAF video quality monitoring system, which controls the picture quality of all encoded videos streamed by Netflix.
Model overview
Images and videos of the three-dimensional visual environments come from a common class: the class of natural scenes. Natural scenes from a tiny subspace in the space of all possible signals, and researchers have developed sophisticated models to characterize these statistics. Most real-world distortion processes disturb these statistics and make the image or video signals unnatural. The VIF index employs natural scene statistical (NSS) models in conjunction with a distortion (channel) model to quantify the information shared between the test and the reference images. Further, the VIF index is based on the hypothesis that this shared information is an aspect of fidelity that relates well with visual quality. In contrast to prior approaches based on human visual system (HVS) error-sensitivity and measurement of structure, this statistical approach used in an information-theoretic setting, yields a full reference (FR) quality assessment (QA) method that does not rely on any HVS or viewing geometry parameter, nor any constants requiring optimization, and yet is competitive with state of the art QA methods.
Specifically, the reference image is modeled as being the output of a stochastic 'natural' source that passes through the HVS channel and is processed later by the brain. The information content of the reference image is quantified as being the mutual information between the input and output of the HVS channel. This is the information that the brain could ideally extract from the output of the HVS. The same measure is then quantified in the presence of an image distortion channel that distorts the output of the natural source before it passes through the HVS channel, thereby measuring the information that the brain could ideally extract from the test image. This is shown pictorially in Figure 1. The two information measures are then combined to form a visual information fidelity measure that relates visual quality to relative image information.
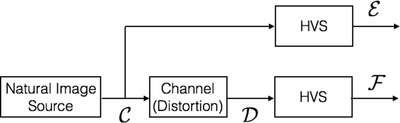
System model
| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (January 2018) (Learn how and when to remove this message) |
Source model
A Gaussian scale mixture (GSM) is used to statistically model the wavelet coefficients of a steerable pyramid decomposition of an image. The model is described below for a given subband of the multi-scale multi-orientation decomposition and can be extended to other subbands similarly. Let the wavelet coefficients in a given subband be where denotes the set of spatial indices across the subband and each is an dimensional vector. The subband is partitioned into non-overlapping blocks of coefficients each, where each block corresponds to . According to the GSM model, where is a positive scalar and is a Gaussian vector with mean zero and co-variance . Further the non-overlapping blocks are assumed to be independent of each other and that the random field is independent of .
Distortion model
The distortion process is modeled using a combination of signal attenuation and additive noise in the wavelet domain. Mathematically, if denotes the random field from a given subband of the distorted image, is a deterministic scalar field and , where is a zero mean Gaussian vector with co-variance , then
Further, is modeled to be independent of and .
HVS model
The duality of HVS models and NSS implies that several aspects of the HVS have already been accounted for in the source model. Here, the HVS is additionally modeled based on the hypothesis that the uncertainty in the perception of visual signals limits the amount of information that can be extracted from the source and distorted image. This source of uncertainty can be modeled as visual noise in the HVS model. In particular, the HVS noise in a given subband of the wavelet decomposition is modeled as additive white Gaussian noise. Let and be random fields, where and are zero mean Gaussian vectors with co-variance and . Further, let and denote the visual signal at the output of the HVS. Mathematically, we have and . Note that and are random fields that are independent of , and .
VIF index
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (January 2018) (Learn how and when to remove this message) |
| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (January 2018) (Learn how and when to remove this message) |
Let denote the vector of all blocks from a given subband. Let and be similarly defined. Let denote the maximum likelihood estimate of given and . The amount of information extracted from the reference is obtained as
while the amount of information extracted from the test image is given as
Denoting the blocks in subband of the wavelet decomposition by , and similarly for the other variables, the VIF index is defined as
Performance
The Spearman's rank-order correlation coefficient (SROCC) between the VIF index scores of distorted images on the LIVE Image Quality Assessment Database and the corresponding human opinion scores is evaluated to be 0.96.
References
- Sheikh, Hamid; Bovik, Alan (2006). "Image Information and Visual Quality". IEEE Transactions on Image Processing. 15 (2): 430–444. Bibcode:2006ITIP...15..430S. doi:10.1109/tip.2005.859378. PMID 16479813.
- Wang, Zhou; Bovik, Alan; Sheikh, Hamid; Simoncelli, Eero (2004). "Image quality assessment: From error visibility to structural similarity". IEEE Transactions on Image Processing. 13 (4): 600–612. Bibcode:2004ITIP...13..600W. doi:10.1109/tip.2003.819861. PMID 15376593. S2CID 207761262.
- Sheikh, Hamid R. (2006). "Image Information and Visual Quality". IEEE Transactions on Image Processing. 15 (2): 430–444. Bibcode:2006ITIP...15..430S. doi:10.1109/tip.2005.859378. PMID 16479813. Retrieved 15 April 2024.
- Simoncelli, Eero; Freeman, William (1995). "The steerable pyramid: A flexible architecture for multi-scale derivative computation". Proceedings., International Conference on Image Processing. Vol. 3. pp. 444–447. doi:10.1109/ICIP.1995.537667. ISBN 0-7803-3122-2. S2CID 1099364.
External links
- Laboratory for Image and Video Engineering at the University of Texas
- An implementation of the VIF index
- LIVE Image Quality Assessment Database
 where
where  denotes the set of spatial indices across the subband and each
denotes the set of spatial indices across the subband and each  is an
is an  dimensional
dimensional  where
where  is a positive
is a positive  is a Gaussian vector with mean zero and
is a Gaussian vector with mean zero and  . Further the non-overlapping blocks are assumed to be independent of each other and that the random field
. Further the non-overlapping blocks are assumed to be independent of each other and that the random field  is independent of
is independent of  .
.
 denotes the random field from a given subband of the distorted image,
denotes the random field from a given subband of the distorted image,  is a
is a  , where
, where  is a zero mean Gaussian vector with co-variance
is a zero mean Gaussian vector with co-variance  , then
, then

 is modeled to be independent of
is modeled to be independent of  and
and  be random fields, where
be random fields, where  and
and  are zero mean Gaussian vectors with co-variance
are zero mean Gaussian vectors with co-variance  and
and  . Further, let
. Further, let  and
and  denote the visual signal at the output of the HVS. Mathematically, we have
denote the visual signal at the output of the HVS. Mathematically, we have  and
and  . Note that
. Note that  and
and  are
are  denote the vector of all blocks from a given subband. Let
denote the vector of all blocks from a given subband. Let  and
and  be similarly defined. Let
be similarly defined. Let  denote the
denote the  given
given  and
and 

 blocks in subband
blocks in subband  of the wavelet decomposition by
of the wavelet decomposition by  , and similarly for the other variables, the VIF index is defined as
, and similarly for the other variables, the VIF index is defined as
