
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion) or it may change (dispersion) while propagating.
Historical background
Ideas related to wave packets – modulation, carrier waves, phase velocity, and group velocity – date from the mid-1800s. The idea of a group velocity distinct from a wave's phase velocity was first proposed by W.R. Hamilton in 1839, and the first full treatment was by Rayleigh in his "Theory of Sound" in 1877.
Erwin Schrödinger introduced the idea of wave packets just after publishing his famous wave equation. He solved his wave equation for a quantum harmonic oscillator, introduced the superposition principle, and used it to show that a compact state could persist. While this work did result in the important concept of coherent states, the wave packet concept did not endure. The year after Schrödinger's paper, Werner Heisenberg published his paper on the uncertainty principle, showing in the process, that Schrödinger's results only applied to quantum harmonic oscillators, not for example to Coulomb potential characteristic of atoms.
The following year, 1927, Charles Galton Darwin explored Schrödinger's equation for an unbound electron in free space, assuming an initial Gaussian wave packet. Darwin showed that at time later the position of the packet traveling at velocity would be
where is the uncertainty in the initial position.
Later in 1927 Paul Ehrenfest showed that the time, for a matter wave packet of width and mass to spread by a factor of 2 was . Since is so small, wave packets on the scale of macroscopic objects, with large width and mass, double only at cosmic time scales.
Significance in quantum mechanics
Quantum mechanics describes the nature of atomic and subatomic systems using Schrödinger's wave equation. The classical limit of quantum mechanics and many formulations of quantum scattering use wave packets formed from various solutions to this equation. Quantum wave packet profiles change while propagating; they show dispersion. Physicists have concluded that "wave packets would not do as representations of subatomic particles".
Wave packets and the classical limit
Schrodinger developed wave packets in hopes of interpreting quantum wave solutions as locally compact wave groups. Such packets tradeoff position localization for spreading momentum. In the coordinate representation of the wave (such as the Cartesian coordinate system), the position of the particle's localized probability is specified by the position of the packet solution. The narrower the spatial wave packet, and therefore the better localized the position of the wave packet, the larger the spread in the momentum of the wave. This trade-off between spread in position and spread in momentum is a characteristic feature of the Heisenberg uncertainty principle.
One kind of optimal tradeoff minimizes the product of position uncertainty and momentum uncertainty . If we place such a packet at rest it stays at rest: the average value of the position and momentum match a classical particle. However it spreads out in all directions with a velocity given by the optimal momentum uncertainty . The spread is so fast that in the distance of once around an atom the wave packet is unrecognizable.
Wave packets and quantum scattering
Particle interactions are called scattering in physics; wave packet mathematics play an important role in quantum scattering approaches. A monochromatic (single momentum) source produces convergence difficulties in the scattering models. Scattering problems also have classical limits. Whenever the scattering target (for example an atom) has a size much smaller than wave packet, the center of the wave packet follows scattering classical trajectories. In other cases, the wave packet distorts and scatters as it interacts with the target.
Basic behaviors
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (October 2024) (Learn how and when to remove this message) |
Non-dispersive

Without dispersion the wave packet maintains its shape as it propagates. As an example of propagation without dispersion, consider wave solutions to the following wave equation from classical physics
where c is the speed of the wave's propagation in a given medium.
Using the physics time convention, e, the wave equation has plane-wave solutions
where the relation between the angular frequency ω and angular wave vector k is given by the dispersion relation: such that . This relation should be valid so that the plane wave is a solution to the wave equation. As the relation is linear, the wave equation is said to be non-dispersive.
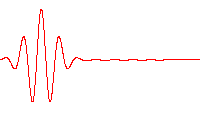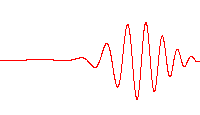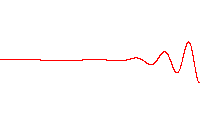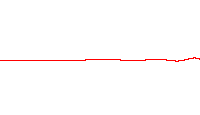
To simplify, consider the one-dimensional wave equation with ω(k) = ±kc. Then the general solution is where the first and second term represent a wave propagating in the positive respectively negative x-direction.
A wave packet is a localized disturbance that results from the sum of many different wave forms. If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region. From the basic one-dimensional plane-wave solutions, a general form of a wave packet can be expressed as where the amplitude A(k), containing the coefficients of the wave superposition, follows from taking the inverse Fourier transform of a "sufficiently nice" initial wave u(x, t) evaluated at t = 0: and comes from Fourier transform conventions.
For example, choosing
we obtain
and finally
The nondispersive propagation of the real or imaginary part of this wave packet is presented in the above animation.
Dispersive

By contrast, in the case of dispersion, a wave changes shape during propagation. For example, the free Schrödinger equation , has plane-wave solutions of the form: where is a constant and the dispersion relation satisfies with the subscripts denoting unit vector notation. As the dispersion relation is non-linear, the free Schrödinger equation is dispersive.
In this case, the wave packet is given by: where once again is simply the Fourier transform of . If (and therefore ) is a Gaussian function, the wave packet is called a Gaussian wave packet.
For example, the solution to the one-dimensional free Schrödinger equation (with 2Δx, m, and ħ set equal to one) satisfying the initial condition representing a wave packet localized in space at the origin as a Gaussian function, is seen to be
An impression of the dispersive behavior of this wave packet is obtained by looking at the probability density: It is evident that this dispersive wave packet, while moving with constant group velocity ko, is delocalizing rapidly: it has a width increasing with time as √ 1 + 4t → 2t, so eventually it diffuses to an unlimited region of space.
Gaussian wave packets in quantum mechanics


The above dispersive Gaussian wave packet, unnormalized and just centered at the origin, instead, at t=0, can now be written in 3D, now in standard units: The Fourier transform is also a Gaussian in terms of the wavenumber, the k-vector, With a and its inverse adhering to the uncertainty relation such that can be considered the square of the width of the wave packet, whereas its inverse can be written as
Each separate wave only phase-rotates in time, so that the time dependent Fourier-transformed solution is
The inverse Fourier transform is still a Gaussian, but now the parameter a has become complex, and there is an overall normalization factor.
The integral of Ψ over all space is invariant, because it is the inner product of Ψ with the state of zero energy, which is a wave with infinite wavelength, a constant function of space. For any energy eigenstate η(x), the inner product, only changes in time in a simple way: its phase rotates with a frequency determined by the energy of η. When η has zero energy, like the infinite wavelength wave, it doesn't change at all.
For a given , the phase of the wave function varies with position as . It varies quadratically with position, which means that it is different from multiplication by a linear phase factor as is the case of imparting a constant momentum to the wave packet. In general, the phase of a gaussian wave packet has both a linear term and a quadratic term. The coefficient of the quadratic term begins by increasing from towards as the gaussian wave packet becomes sharper, then at the moment of maximum sharpness, the phase of the wave function varies linearly with position. Then the coefficient of the quadratic term increases from towards , as the gaussian wave packet spreads out again.
The integral ∫ |Ψ|dr is also invariant, which is a statement of the conservation of probability. Explicitly, where r is the distance from the origin, the speed of the particle is zero, and width given by which is √a at (arbitrarily chosen) time t = 0 while eventually growing linearly in time, as ħt/(m√a), indicating wave-packet spreading.
For example, if an electron wave packet is initially localized in a region of atomic dimensions (i.e., 10 m) then the width of the packet doubles in about 10 s. Clearly, particle wave packets spread out very rapidly indeed (in free space): For instance, after 1 ms, the width will have grown to about a kilometer.
This linear growth is a reflection of the (time-invariant) momentum uncertainty: the wave packet is confined to a narrow Δx = √a/2, and so has a momentum which is uncertain (according to the uncertainty principle) by the amount ħ/√2a, a spread in velocity of ħ/m√2a, and thus in the future position by ħt /m√2a. The uncertainty relation is then a strict inequality, very far from saturation, indeed! The initial uncertainty ΔxΔp = ħ/2 has now increased by a factor of ħt/ma (for large t).
The 2D case

A gaussian 2D quantum wave function:
where
The Airy wave train
In contrast to the above Gaussian wave packet, which moves at constant group velocity, and always disperses, there exists a wave function based on Airy functions, that propagates freely without envelope dispersion, maintaining its shape, and accelerates in free space: where, for simplicity (and nondimensionalization), chosing ħ = 1, m = 1/2, and B an arbitrary constant results in
There is no dissonance with Ehrenfest's theorem in this force-free situation, because the state is both non-normalizable and has an undefined (infinite) ⟨x⟩ for all times. (To the extent that it could be defined, ⟨p⟩ = 0 for all times, despite the apparent acceleration of the front.)
The Airy wave train is the only dispersionless wave in one dimensional free space. In higher dimensions, other dispersionless waves are possible.
In phase space, this is evident in the pure state Wigner quasiprobability distribution of this wavetrain, whose shape in x and p is invariant as time progresses, but whose features accelerate to the right, in accelerating parabolas. The Wigner function satisfiesThe three equalities demonstrate three facts:
- Time-evolution is equivalent to a translation in phase-space by .
- The contour lines of the Wigner function are parabolas of form .
- Time-evolution is equivalent to a shearing in phase space along the -direction at speed .
Note the momentum distribution obtained by integrating over all x is constant. Since this is the probability density in momentum space, it is evident that the wave function itself is not normalizable.
Free propagator
The narrow-width limit of the Gaussian wave packet solution discussed is the free propagator kernel K. For other differential equations, this is usually called the Green's function, but in quantum mechanics it is traditional to reserve the name Green's function for the time Fourier transform of K.
Returning to one dimension for simplicity, with m and ħ set equal to one, when a is the infinitesimal quantity ε, the Gaussian initial condition, rescaled so that its integral is one, becomes a delta function, δ(x), so that its time evolution, yields the propagator.
Note that a very narrow initial wave packet instantly becomes infinitely wide, but with a phase which is more rapidly oscillatory at large values of x. This might seem strange—the solution goes from being localized at one point to being "everywhere" at all later times, but it is a reflection of the enormous momentum uncertainty of a localized particle, as explained above.
Further note that the norm of the wave function is infinite, which is also correct, since the square of a delta function is divergent in the same way.
The factor involving ε is an infinitesimal quantity which is there to make sure that integrals over K are well defined. In the limit that ε → 0, K becomes purely oscillatory, and integrals of K are not absolutely convergent. In the remainder of this section, it will be set to zero, but in order for all the integrations over intermediate states to be well defined, the limit ε→0 is to be only taken after the final state is calculated.
The propagator is the amplitude for reaching point x at time t, when starting at the origin, x=0. By translation invariance, the amplitude for reaching a point x when starting at point y is the same function, only now translated,
In the limit when t is small, the propagator goes to a delta function but only in the sense of distributions: The integral of this quantity multiplied by an arbitrary differentiable test function gives the value of the test function at zero.
To see this, note that the integral over all space of K equals 1 at all times, since this integral is the inner-product of K with the uniform wave function. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit ε→0 is taken at the very end.
So the propagation kernel is the (future) time evolution of a delta function, and it is continuous, in a sense: it goes to the initial delta function at small times. If the initial wave function is an infinitely narrow spike at position y, it becomes the oscillatory wave,
Now, since every function can be written as a weighted sum of such narrow spikes, the time evolution of every function ψ0 is determined by this propagation kernel K,
Thus, this is a formal way to express the fundamental solution or general solution. The interpretation of this expression is that the amplitude for a particle to be found at point x at time t is the amplitude that it started at y, times the amplitude that it went from y to x, summed over all the possible starting points. In other words, it is a convolution of the kernel K with the arbitrary initial condition ψ0,
Since the amplitude to travel from x to y after a time t+t' can be considered in two steps, the propagator obeys the composition identity, which can be interpreted as follows: the amplitude to travel from x to z in time t+t' is the sum of the amplitude to travel from x to y in time t, multiplied by the amplitude to travel from y to z in time t', summed over all possible intermediate states y. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a path integral.
Analytic continuation to diffusion
See also: Heat equation § Fundamental solutionsThe spreading of wave packets in quantum mechanics is directly related to the spreading of probability densities in diffusion. For a particle which is randomly walking, the probability density function satisfies the diffusion equation where the factor of 2, which can be removed by rescaling either time or space, is only for convenience.
A solution of this equation is the time-varying Gaussian function which is a form of the heat kernel. Since the integral of ρt is constant while the width is becoming narrow at small times, this function approaches a delta function at t=0, again only in the sense of distributions, so that for any test function f.
The time-varying Gaussian is the propagation kernel for the diffusion equation and it obeys the convolution identity, which allows diffusion to be expressed as a path integral. The propagator is the exponential of an operator H, which is the infinitesimal diffusion operator,
A matrix has two indices, which in continuous space makes it a function of x and x'. In this case, because of translation invariance, the matrix element K only depend on the difference of the position, and a convenient abuse of notation is to refer to the operator, the matrix elements, and the function of the difference by the same name:
Translation invariance means that continuous matrix multiplication, is essentially convolution,
The exponential can be defined over a range of ts which include complex values, so long as integrals over the propagation kernel stay convergent, As long as the real part of z is positive, for large values of x, K is exponentially decreasing, and integrals over K are indeed absolutely convergent.
The limit of this expression for z approaching the pure imaginary axis is the above Schrödinger propagator encountered, which illustrates the above time evolution of Gaussians.
From the fundamental identity of exponentiation, or path integration, holds for all complex z values, where the integrals are absolutely convergent so that the operators are well defined.
Thus, quantum evolution of a Gaussian, which is the complex diffusion kernel K, amounts to the time-evolved state,
This illustrates the above diffusive form of the complex Gaussian solutions,
See also
- Wave
- Wave propagation
- Fourier analysis
- Group velocity
- Phase velocity
- Free particle
- Coherent states
- Waveform
- Wavelet
- Matter wave
- Pulse (signal processing)
- Pulse (physics)
- Schrödinger equation
- Introduction to quantum mechanics
- Soliton
Notes
- Joy Manners (2000), Quantum Physics: An Introduction, CRC Press, pp. 53–56, ISBN 978-0-7503-0720-8
- Schwartz, Matthew. "Lecture 11: Wavepackets and dispersion" (PDF). scholar.harvard.edu. Archived (PDF) from the original on 2023-03-18. Retrieved 2023-06-22.
- Brillouin, Léon (1960), Wave Propagation and Group Velocity, New York: Academic Press Inc., OCLC 537250
- ^ Kragh, Helge (2009). "Wave Packet". In Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (eds.). Compendium of Quantum Physics. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 828–830. doi:10.1007/978-3-540-70626-7_232. ISBN 978-3-540-70622-9.
- Darwin, Charles Galton. "Free motion in the wave mechanics." Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 117.776 (1927): 258-293.
- Schiff, Leonard I. (1995). Quantum mechanics. International series in pure and applied physics (3. ed., 29. print ed.). New York: McGraw-Hill. ISBN 978-0-07-055287-6.
- Newton, Roger G. (1982). Scattering theory of waves and particles. Texts and monographs in physics (2 ed.). New York, Heidelberg, Berlin: Springer. ISBN 978-0-387-10950-3.
- Susskind, Leonard; Friedman, Art; Susskind, Leonard (2014). Quantum mechanics: the theoretical minimum; . The theoretical minimum / Leonard Susskind and George Hrabovsky. New York, NY: Basic Books. ISBN 978-0-465-08061-8.
- Jackson 1998, pp. 322–326.
- Hall, Brian C. (2013). Quantum Theory for Mathematicians. New York Heidelberg Dordrecht London: Springer. pp. 91–92. ISBN 978-1-4614-7115-8.
- Cohen-Tannoudji, Diu & Laloë 2019, pp. 13–15.
- Cohen-Tannoudji, Diu & Laloë 2019, pp. 57, 1511.
- Pauli, Wolfgang (2000), Wave Mechanics: Volume 5 of Pauli Lectures on Physics, Books on Physics, Dover Publications, pp. 7–10, ISBN 978-0-486-41462-1
- * Abers, E.; Pearson, Ed (2004), Quantum Mechanics, Addison Wesley, Prentice-Hall Inc., p. 51, ISBN 978-0-13-146100-0
- Cohen-Tannoudji, Diu & Laloë 2019, pp. 237–240.
- Darwin, C. G. (1927). "Free motion in the wave mechanics", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 117 (776), 258-293.
- Richard Fitzpatrick, Oscillations and Waves
- Cohen-Tannoudji, Diu & Laloë 2019, p. 59.
- Berry, M. V.; Balazs, N. L. (1979), "Nonspreading wave packets", Am J Phys, 47 (3): 264–267, Bibcode:1979AmJPh..47..264B, doi:10.1119/1.11855
- Unnikrishnan, K.; Rau, A. R. P. (1996-08-01). "Uniqueness of the Airy packet in quantum mechanics". American Journal of Physics. 64 (8): 1034–1035. doi:10.1119/1.18322. ISSN 0002-9505.
- Efremidis, Nikolaos K.; Chen, Zhigang; Segev, Mordechai; Christodoulides, Demetrios N. (2019-05-20). "Airy beams and accelerating waves: an overview of recent advances". Optica. 6 (5): 686. arXiv:1904.02933. doi:10.1364/OPTICA.6.000686. ISSN 2334-2536.
- Jackson 1998, pp. 38–39.
- Feynman, R. P.; Hibbs, A. R. (1965), Quantum Mechanics and Path Integrals, New York: McGraw-Hill, ISBN 978-0-07-020650-2
- Kozdron 2008, chpt. 3 Albert Einstein's proof of the existence of Brownian motion.
References
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2019). Quantum Mechanics, Volume 1. Weinheim, Germany: John Wiley & Sons. ISBN 978-3-527-34553-3.
- Jackson, John David (1998). Classical Electrodynamics. New York: John Wiley & Sons. ISBN 978-0-471-30932-1.
- Kozdron, Michael J. (2008). "Brownian Motion and the Heat Equation" (PDF). University of Regina. Retrieved October 29, 2024.
External links
 Learning materials related to wave packet motion at Wikiversity
Learning materials related to wave packet motion at Wikiversity The dictionary definition of wave packet at Wiktionary
The dictionary definition of wave packet at Wiktionary- 1d Wave packet plot in Google
- 1d Wave train and probability density plot in Google
- 2d Wave packet plot in Google
- 2d Wave train plot in Google
- 2d probability density plot in Google
- Quantum physics online : Interactive simulation of a free wavepacket
- Web-Schrödinger: Interactive 2D wave packet dynamics simulation
- A simulation of a wave package in 2D (According to FOURIER-Synthesis in 2D)
 later the position
later the position  of the packet traveling at velocity
of the packet traveling at velocity  would be
would be

 is the uncertainty in the initial position.
is the uncertainty in the initial position.
 for a
for a  and mass
and mass  to spread by a factor of 2 was
to spread by a factor of 2 was  . Since
. Since  is so small, wave packets on the scale of macroscopic objects, with large width and mass, double only at cosmic time scales.
is so small, wave packets on the scale of macroscopic objects, with large width and mass, double only at cosmic time scales.
 . If we place such a packet at rest it stays at rest: the average value of the position and momentum match a classical particle. However it spreads out in all directions with a velocity given by the optimal momentum uncertainty
. If we place such a packet at rest it stays at rest: the average value of the position and momentum match a classical particle. However it spreads out in all directions with a velocity given by the optimal momentum uncertainty 

 such that
such that  . This relation should be valid so that the plane wave is a solution to the wave equation. As the relation is linear, the wave equation is said to be non-dispersive.
. This relation should be valid so that the plane wave is a solution to the wave equation. As the relation is linear, the wave equation is said to be non-dispersive.
 where the first and second term represent a wave propagating in the positive respectively negative x-direction.
where the first and second term represent a wave propagating in the positive respectively negative x-direction.
 where the amplitude A(k), containing the coefficients of the
where the amplitude A(k), containing the coefficients of the  and
and  comes from
comes from 


 has plane-wave solutions of the form:
has plane-wave solutions of the form:
 where
where  is a constant and the dispersion relation satisfies
is a constant and the dispersion relation satisfies
 with the subscripts denoting
with the subscripts denoting  where once again
where once again  is simply the Fourier transform of
is simply the Fourier transform of  . If
. If  representing a wave packet localized in space at the origin as a Gaussian function, is seen to be
representing a wave packet localized in space at the origin as a Gaussian function, is seen to be

 It is evident that this dispersive wave packet, while moving with constant group velocity ko, is delocalizing rapidly: it has a
It is evident that this dispersive wave packet, while moving with constant group velocity ko, is delocalizing rapidly: it has a  The Fourier transform is also a Gaussian in terms of the wavenumber, the k-vector,
The Fourier transform is also a Gaussian in terms of the wavenumber, the k-vector,
 With a and its inverse adhering to the
With a and its inverse adhering to the  such that
such that
 can be considered the square of the width of the wave packet, whereas its inverse can be written as
can be considered the square of the width of the wave packet, whereas its inverse can be written as

 . The group velocity is zero. At
. The group velocity is zero. At  , the wavefunction has zero phase and minimal width. For
, the wavefunction has zero phase and minimal width. For  , the wavefunction has quadratic phase, decreasing width. For
, the wavefunction has quadratic phase, decreasing width. For  , the wavefunction has quadratic phase, increasing width.
, the wavefunction has quadratic phase, increasing width.
 . The overall group velocity is positive, and the wave packet moves as it disperses.
. The overall group velocity is positive, and the wave packet moves as it disperses.
 only changes in time in a simple way: its phase rotates with a frequency determined by the energy of η. When η has zero energy, like the infinite wavelength wave, it doesn't change at all.
only changes in time in a simple way: its phase rotates with a frequency determined by the energy of η. When η has zero energy, like the infinite wavelength wave, it doesn't change at all.
 . It varies quadratically with position, which means that it is different from multiplication by a linear
. It varies quadratically with position, which means that it is different from multiplication by a linear  as is the case of imparting a constant momentum to the wave packet. In general, the phase of a gaussian wave packet has both a linear term and a quadratic term. The coefficient of the quadratic term begins by increasing from
as is the case of imparting a constant momentum to the wave packet. In general, the phase of a gaussian wave packet has both a linear term and a quadratic term. The coefficient of the quadratic term begins by increasing from  towards
towards  as the gaussian wave packet becomes sharper, then at the moment of maximum sharpness, the phase of the wave function varies linearly with position. Then the coefficient of the quadratic term increases from
as the gaussian wave packet becomes sharper, then at the moment of maximum sharpness, the phase of the wave function varies linearly with position. Then the coefficient of the quadratic term increases from  , as the gaussian wave packet spreads out again.
, as the gaussian wave packet spreads out again.
 where r is the distance from the origin, the speed of the particle is zero, and width given by
where r is the distance from the origin, the speed of the particle is zero, and width given by
 which is √a at (arbitrarily chosen) time t = 0 while eventually growing linearly in time, as ħt/(m√a), indicating wave-packet spreading.
which is √a at (arbitrarily chosen) time t = 0 while eventually growing linearly in time, as ħt/(m√a), indicating wave-packet spreading.
 , its brightness indicates
, its brightness indicates  .
.  ,
, 




 where, for simplicity (and
where, for simplicity (and 
 The three equalities demonstrate three facts:
The three equalities demonstrate three facts:
 .
. .
. .
. becomes a
becomes a  yields the propagator.
yields the propagator.

 but only in the sense of
but only in the sense of  since this integral is the inner-product of K with the uniform wave function. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit ε→0 is taken at the very end.
since this integral is the inner-product of K with the uniform wave function. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit ε→0 is taken at the very end.
 it becomes the oscillatory wave,
it becomes the oscillatory wave,

 the time evolution of every function ψ0 is determined by this propagation kernel K,
the time evolution of every function ψ0 is determined by this propagation kernel K,


 which can be interpreted as follows: the amplitude to travel from x to z in time t+t' is the sum of the amplitude to travel from x to y in time t, multiplied by the amplitude to travel from y to z in time t', summed over all possible intermediate states y. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a
which can be interpreted as follows: the amplitude to travel from x to z in time t+t' is the sum of the amplitude to travel from x to y in time t, multiplied by the amplitude to travel from y to z in time t', summed over all possible intermediate states y. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a  where the factor of 2, which can be removed by rescaling either time or space, is only for convenience.
where the factor of 2, which can be removed by rescaling either time or space, is only for convenience.
 which is a form of the
which is a form of the  again only in the sense of distributions, so that
again only in the sense of distributions, so that
 for any
for any  which allows diffusion to be expressed as a path integral. The propagator is the exponential of an operator H,
which allows diffusion to be expressed as a path integral. The propagator is the exponential of an operator H,
 which is the infinitesimal diffusion operator,
which is the infinitesimal diffusion operator,


 is essentially convolution,
is essentially convolution,

 As long as the real part of z is positive, for large values of x, K is exponentially decreasing, and integrals over K are indeed absolutely convergent.
As long as the real part of z is positive, for large values of x, K is exponentially decreasing, and integrals over K are indeed absolutely convergent.
 which illustrates the above time evolution of Gaussians.
which illustrates the above time evolution of Gaussians.
 holds for all complex z values, where the integrals are absolutely convergent so that the operators are well defined.
holds for all complex z values, where the integrals are absolutely convergent so that the operators are well defined.
 amounts to the time-evolved state,
amounts to the time-evolved state,

