
A Wien bridge oscillator is a type of electronic oscillator that generates sine waves. It can generate a large range of frequencies. The oscillator is based on a bridge circuit originally developed by Max Wien in 1891 for the measurement of impedances. The bridge comprises four resistors and two capacitors. The oscillator can also be viewed as a positive gain amplifier combined with a bandpass filter that provides positive feedback. Automatic gain control, intentional non-linearity and incidental non-linearity limit the output amplitude in various implementations of the oscillator.
The circuit shown to the right depicts a once-common implementation of the oscillator, with automatic gain control using an incandescent lamp. Under the condition that R1=R2=R and C1=C2=C, the frequency of oscillation is given by:
and the condition of stable oscillation is given by
Background
There were several efforts to improve oscillators in the 1930s. Linearity was recognized as important. The "resistance-stabilized oscillator" had an adjustable feedback resistor; that resistor would be set so the oscillator just started (thus setting the loop gain to just over unity). The oscillations would build until the vacuum tube's grid would start conducting current, which would increase losses and limit the output amplitude. Automatic amplitude control was investigated. Frederick Terman states, "The frequency stability and wave-shape form of any common oscillator can be improved by using an automatic-amplitude-control arrangement to maintain the amplitude of oscillations constant under all conditions."
In 1937, Larned Meacham described using a filament lamp for automatic gain control in bridge oscillators.
Also in 1937, Hermon Hosmer Scott described audio oscillators based on various bridges including the Wien bridge.
Terman, at Stanford University, was interested in Harold Stephen Black's work on negative feedback, so he held a graduate seminar on negative feedback. Bill Hewlett attended the seminar. Scott's February 1938 oscillator paper came out during the seminar. Here is a recollection by Terman:
- Fred Terman explains: "To complete the requirements for an Engineer's degree at Stanford, Bill had to prepare a thesis. At that time I had decided to devote an entire quarter of my graduate seminar to the subject of 'negative feedback' I had become interested in this then new technique because it seemed to have great potential for doing many useful things. I would report on some applications I had thought up on negative feedback, and the boys would read recent articles and report to each other on current developments. This seminar was just well started when a paper came out that looked interesting to me. It was by a man from General Radio and dealt with a fixed-frequency audio oscillator in which the frequency was controlled by a resistance-capacitance network, and was changed by means of push-buttons. Oscillations were obtained by an ingenious application of negative feedback."
In June 1938, Terman, R. R. Buss, Hewlett and F. C. Cahill gave a presentation about negative feedback at the IRE Convention in New York; in August 1938, there was a second presentation at the IRE Pacific Coast Convention in Portland, OR; the presentation became an IRE paper. One topic was amplitude control in a Wien bridge oscillator. The oscillator was demonstrated in Portland. Hewlett, along with David Packard, co-founded Hewlett-Packard, and Hewlett-Packard's first product was the HP200A, a precision Wien bridge oscillator. The first sale was in January 1939.
Hewlett's June 1939 engineer's degree thesis used a lamp to control the amplitude of a Wien bridge oscillator. Hewlett's oscillator produced a sinusoidal output with a stable amplitude and low distortion.
Oscillators without automatic gain control

The conventional oscillator circuit is designed so that it will start oscillating ("start up") and that its amplitude will be controlled.
The oscillator at the right uses diodes to add a controlled compression to the amplifier output. It can produce total harmonic distortion in the range of 1-5%, depending on how carefully it is trimmed.
For a linear circuit to oscillate, it must meet the Barkhausen conditions: its loop gain must be one and the phase around the loop must be an integer multiple of 360 degrees. The linear oscillator theory doesn't address how the oscillator starts up or how the amplitude is determined. The linear oscillator can support any amplitude.
In practice, the loop gain is initially larger than unity. Random noise is present in all circuits, and some of that noise will be near the desired frequency. A loop gain greater than one allows the amplitude of frequency to increase exponentially each time around the loop. With a loop gain greater than one, the oscillator will start.
Ideally, the loop gain needs to be just a little bigger than one, but in practice, it is often significantly greater than one. A larger loop gain makes the oscillator start quickly. A large loop gain also compensates for gain variations with temperature and the desired frequency of a tunable oscillator. For the oscillator to start, the loop gain must be greater than one under all possible conditions.
A loop gain greater than one has a down side. In theory, the oscillator amplitude will increase without limit. In practice, the amplitude will increase until the output runs into some limiting factor such as the power supply voltage (the amplifier output runs into the supply rails) or the amplifier output current limits. The limiting reduces the effective gain of the amplifier (the effect is called gain compression). In a stable oscillator, the average loop gain will be one.
Although the limiting action stabilizes the output voltage, it has two significant effects: it introduces harmonic distortion and it affects the frequency stability of the oscillator.
The amount of distortion is related to the extra loop gain used for startup. If there's a lot of extra loop gain at small amplitudes, then the gain must decrease more at higher instantaneous amplitudes. That means more distortion.
The amount of distortion is also related to final amplitude of the oscillation. Although an amplifier's gain is ideally linear, in practice it is nonlinear. The nonlinear transfer function can be expressed as a Taylor series. For small amplitudes, the higher order terms have little effect. For larger amplitudes, the nonlinearity is pronounced. Consequently, for low distortion, the oscillator's output amplitude should be a small fraction of the amplifier's dynamic range.
Meacham's bridge stabilized oscillator

Larned Meacham disclosed the bridge oscillator circuit shown to the right in 1938. The circuit was described as having very high frequency stability and very pure sinusoidal output. Instead of using tube overloading to control the amplitude, Meacham proposed a circuit that set the loop gain to unity while the amplifier is in its linear region. Meacham's circuit included a quartz crystal oscillator and a lamp in a Wheatstone bridge.
In Meacham's circuit, the frequency determining components are in the negative feed back branch of the bridge and the gain controlling elements are in the positive feed back branch. The crystal, Z4, operates in series resonance. As such it minimizes the negative feedback at resonance. The particular crystal exhibited a real resistance of 114 ohms at resonance. At frequencies below resonance, the crystal is capacitive and the gain of the negative feedback branch has a negative phase shift. At frequencies above resonance, the crystal is inductive and the gain of the negative feedback branch has a positive phase shift. The phase shift goes through zero at the resonant frequency. As the lamp heats up, it decreases the positive feedback. The Q of the crystal in Meacham's circuit is given as 104,000. At any frequency different from the resonant frequency by more than a small multiple of the bandwidth of the crystal, the negative feedback branch dominates the loop gain and there can be no self-sustaining oscillation except within the narrow bandwidth of the crystal.
In 1944 (after Hewlett's design), J. K. Clapp modified Meacham's circuit to use a vacuum tube phase inverter instead of a transformer to drive the bridge. A modified Meacham oscillator uses Clapp's phase inverter but substitutes a diode limiter for the tungsten lamp.
Hewlett's oscillator

William R. Hewlett's Wien bridge oscillator can be considered as a combination of a differential amplifier and a Wien bridge, connected in a positive feedback loop between the amplifier output and differential inputs. At the oscillating frequency, the bridge is almost balanced and has very small transfer ratio. The loop gain is a product of the very high amplifier gain and the very low bridge ratio. In Hewlett's circuit, the amplifier is implemented by two vacuum tubes. The amplifier's inverting input is the cathode of tube V1 and the non-inverting input is the control grid of tube V2. To simplify analysis, all the components other than R1, R2, C1 and C2 can be modeled as a non-inverting amplifier with a gain of 1+Rf/Rb and with a high input impedance. R1, R2, C1 and C2 form a bandpass filter which is connected to provide positive feedback at the frequency of oscillation. Rb self heats and increases the negative feedback which reduces the amplifier gain until the point is reached that there is just enough gain to sustain sinusoidal oscillation without over driving the amplifier. If R1 = R2 and C1 = C2 then at equilibrium Rf/Rb = 2 and the amplifier gain is 3. When the circuit is first energized, the lamp is cold and the gain of the circuit is greater than 3 which ensures start up. The dc bias current of vacuum tube V1 also flows through the lamp. This does not change the principles of the circuit's operation, but it does reduce the amplitude of the output at equilibrium because the bias current provides part of the heating of the lamp.
Hewlett's thesis made the following conclusions:
- A resistance-capacity oscillator of the type just described should be well suited for laboratory service. It has the ease of handling of a beat-frequency oscillator and yet few of its disadvantages. In the first place the frequency stability at low frequencies is much better than is possible with the beat-frequency type. There need be no critical placements of parts to insure small temperature changes, nor carefully designed detector circuits to prevent interlocking of oscillators. As a result of this, the overall weight of the oscillator may be kept at a minimum. An oscillator of this type, including a 1 watt amplifier and power supply, weighed only 18 pounds, in contrast to 93 pounds for the General Radio beat-frequency oscillator of comparable performance. The distortion and constancy of output compare favorably with the best beat-frequency oscillators now available. Lastly, an oscillator of this type can be laid out and constructed on the same basis as a commercial broadcast receiver, but with fewer adjustments to make. It thus combines quality of performance with cheapness of cost to give an ideal laboratory oscillator.
Wien bridge
Main article: Wien bridgeBridge circuits were a common way of measuring component values by comparing them to known values. Often an unknown component would be put in one arm of a bridge, and then the bridge would be nulled by adjusting the other arms or changing the frequency of the voltage source (see, for example, the Wheatstone bridge).
The Wien bridge is one of many common bridges. Wien's bridge is used for precision measurement of capacitance in terms of resistance and frequency. It was also used to measure audio frequencies.
The Wien bridge does not require equal values of R or C. The phase of the signal at Vp relative to the signal at Vout varies from almost 90° leading at low frequency to almost 90° lagging at high frequency. At some intermediate frequency, the phase shift will be zero. At that frequency the ratio of Z1 to Z2 will be purely real (zero imaginary part). If the ratio of Rb to Rf is adjusted to the same ratio, then the bridge is balanced and the circuit can sustain oscillation. The circuit will oscillate even if Rb / Rf has a small phase shift and even if the inverting and non-inverting inputs of the amplifier have different phase shifts. There will always be a frequency at which the total phase shift of each branch of the bridge will be equal. If Rb / Rf has no phase shift and the phase shifts of the amplifiers inputs are zero then the bridge is balanced when:
- and
where ω is the radian frequency.
If one chooses R1 = R2 and C1 = C2 then Rf = 2 Rb.
In practice, the values of R and C will never be exactly equal, but the equations above show that for fixed values in the Z1 and Z2 impedances, the bridge will balance at some ω and some ratio of Rb/Rf.
Analysis
Analyzed from loop gain
According to Schilling, the loop gain of the Wien bridge oscillator, under the condition that R1=R2=R and C1=C2=C, is given by
where is the frequency-dependent gain of the op-amp (note, the component names in Schilling have been replaced with the component names in the first figure).
Schilling further says that the condition of oscillation is T=1 which, is satisfied by
and
- with
Another analysis, with particular reference to frequency stability and selectivity, is in Strauss (1970, p. 671) and Hamilton (2003, p. 449).
Frequency determining network
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (September 2015) (Learn how and when to remove this message) |
Let R=R1=R2 and C=C1=C2
Normalize to CR=1.
Thus the frequency determining network has a zero at 0 and poles at or −2.6180 and −0.38197.
Amplitude stabilization
The key to the Wien bridge oscillator's low distortion oscillation is an amplitude stabilization method that does not use clipping. The idea of using a lamp in a bridge configuration for amplitude stabilization was published by Meacham in 1938. The amplitude of electronic oscillators tends to increase until clipping or other gain limitation is reached. This leads to high harmonic distortion, which is often undesirable.
Hewlett used an incandescent bulb as a power detector, low pass filter and gain control element in the oscillator feedback path to control the output amplitude. The resistance of the light bulb filament (see resistivity article) increases as its temperature increases. The temperature of the filament depends on the power dissipated in the filament and some other factors. If the oscillator's period (an inverse of its frequency) is significantly shorter than the thermal time constant of the filament, then the temperature of the filament will be substantially constant over a cycle. The filament resistance will then determine the amplitude of the output signal. If the amplitude increases, the filament heats up and its resistance increases. The circuit is designed so that a larger filament resistance reduces loop gain, which in turn will reduce the output amplitude. The result is a negative feedback system that stabilizes the output amplitude to a constant value. With this form of amplitude control, the oscillator operates as a near ideal linear system and provides a very low distortion output signal. Oscillators that use limiting for amplitude control often have significant harmonic distortion. At low frequencies, as the time period of the Wien bridge oscillator approaches the thermal time constant of the incandescent bulb, the circuit operation becomes more nonlinear, and the output distortion rises significantly.
Light bulbs have their disadvantages when used as gain control elements in Wien bridge oscillators, most notably a very high sensitivity to vibration due to the bulb's microphonic nature amplitude modulating the oscillator output, a limitation in high frequency response due to the inductive nature of the coiled filament, and current requirements that exceed the capability of many op-amps. Modern Wien bridge oscillators have used other nonlinear elements, such as diodes, thermistors, field effect transistors, or photocells for amplitude stabilization in place of light bulbs. Distortion as low as 0.0003% (3 ppm) can be achieved with modern components unavailable to Hewlett.
Wien bridge oscillators that use thermistors exhibit extreme sensitivity to ambient temperature due to the low operating temperature of a thermistor compared to an incandescent lamp.
Automatic gain control dynamics
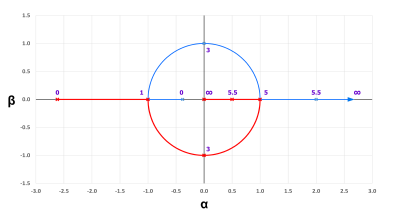
Small perturbations in the value of Rb cause the dominant poles to move back and forth across the jω (imaginary) axis. If the poles move into the left half plane, the oscillation dies out exponentially to zero. If the poles move into the right half plane, the oscillation grows exponentially until something limits it. If the perturbation is very small, the magnitude of the equivalent Q is very large so that the amplitude changes slowly. If the perturbations are small and reverse after a short time, the envelope follows a ramp. The envelope is approximately the integral of the perturbation. The perturbation to envelope transfer function rolls off at 6 dB/octave and causes −90° of phase shift.
The light bulb has thermal inertia so that its power to resistance transfer function exhibits a single pole low pass filter. The envelope transfer function and the bulb transfer function are effectively in cascade, so that the control loop has effectively a low pass pole and a pole at zero and a net phase shift of almost −180°. This would cause poor transient response in the control loop due to low phase margin. The output might exhibit squegging. Bernard M. Oliver showed that slight compression of the gain by the amplifier mitigates the envelope transfer function so that most oscillators show good transient response, except in the rare case where non-linearity in the vacuum tubes canceled each other producing an unusually linear amplifier.
References
- Wien 1891
- Terman 1933
- Terman 1935, pp. 283–289
- Terman 1937, pp. 371–372
- Arguimbau 1933
- Groszkowski 1934
- Terman 1937, p. 370
- Meacham 1939
- ^ Meacham 1938
- Scott 1939
- Scott 1938
- Black 1934a
- Black 1934b
- HP 2002
- Sharpe n.d.
- Terman et al. 1939
- Sharpe n.d., p. ???; Packard remembers first demonstration of the 200A in Portland.
- Sharpe n.d., p. xxx
- Williams (1991, p. 46) states, "Hewlett may have adapted this technique from Meacham, who published it in 1938 as a way to stabilize a quartz crystal oscillator. Meacham's paper, "The Bridge Stabilized Oscillator," is in reference number five in Hewlett's thesis."
- Hewlett 1942
- Williams 1991, pp. 46–47
- Graeme, Jerald G.; Tobey, Gene E.; Huelsman, Lawrence P. (1971). Operational Amplifiers, Design and Applications (1st ed.). McGraw-Hill. pp. 383–385. ISBN 0-07-064917-0.
- Clapp 1944a
- Clapp 1944b
- Matthys 1992, pp. 53–57
- ^ Schilling & Belove 1968, pp. 612–614
- Hewlett 1939, p. 13
- Terman 1943, p. 904
- Terman 1943, p. 904 citing Ferguson & Bartlett 1928
- Terman 1943, p. 905
- Meacham 1938. Meacham1938a. Meacham presented his work at the Thirteenth Annual Convention of the Institute of Radio Engineers, New York City, June 16, 1938 and published in Proc. IRE October 1938. Hewlett's patent (filed July 11, 1939) does not mention Meacham.
- Williams 1990, pp. 32–33
- Strauss 1970, p. 710, stating "For acceptable amplitude stability, some form of temperature compensation would be necessary."
- Strauss 1970, p. 667
- Oliver 1960
Other references
- Arguimbau, L. B. (January 1933), "An Oscillator Having a Linear Operating Characteristic", Proceedings of the I.R.E., 21: 14
- Bauer, Brunton (November 1949a), "Design Notes on the Resistance-Capacity Oscillator Circuit (Part I)" (PDF), Hewlett-Packard Journal, 1 (3), Hewlett-Packard Company
- Bauer, Brunton (December 1949b), "Design Notes on the Resistance-Capacity Oscillator Circuit (Part II)" (PDF), Hewlett-Packard Journal, 1 (4), Hewlett-Packard Company
- Black, H. S. (January 1934a), "Stabilized feedback amplifier", Radio Engineer, 53: 114–120
- Black, H. S. (January 1934b), "Stabilized feedback amplifier", Bell System Technical Journal, 13 (1): 1–18, doi:10.1002/j.1538-7305.1934.tb00652.x
- Ferguson, J. G.; Bartlett, B. W. (July 1928), "The Measurement of Capacitance in Terms of Resistance and Frequency" (PDF), Bell System Technical Journal, 7 (3): 420–437, doi:10.1002/j.1538-7305.1928.tb01234.x
- Clapp, J. K. (April 1944a), "A Bridge-Controlled Oscillator" (PDF), The General Radio Experimenter, XVIII (11): 1–4
- Clapp, J. K. (May 1944b), "An Analysis of the Bridge-Controlled Oscillator" (PDF), The General Radio Experimenter, XVIII (12): 6–8
- Groszkowski, Janusz (February 1934), "Oscillators with Automatic Control of the Threshold of Regenerations", Proceedings of the I.R.E., 22: 145
- Hamilton, Scott (2003), An Analog Electronics Companion: basic circuit design for engineers and scientists, Cambridge University Press, ISBN 978-0-521-79838-9
- Hamilton, Scott (2007), An Analog Electronics Companion: basic circuit design for engineers and scientists and introduction to SPICE simulation, Cambridge University Press, ISBN 978-0-521-68780-5
- Hewlett, William Redington (June 1939), A New Type Resistance-Capacity Oscillator, Engineer's Thesis, Stanford University
- US 2268872, Hewlett, William R., "Variable Frequency Oscillation Generator", published July 11, 1939, issued January 6, 1942
- HP (22 January 2002), A real gem: HP's audio oscillator patent turns 60, HP; Speaks of Terman's inspiration by Black and his late 1930s graduate seminar about negative feedback and fixed-frequency audio oscillators; Hewlett finishing masters and looking for engineers thesis; hiring San Francisco patent attorney in 1939.
- Meacham, L. A. (October 1938a), "The Bridge Stabilized Oscillator", Proc. IRE, 26 (10): 1278–1294, doi:10.1109/jrproc.1938.228725, S2CID 51651042
- Meacham, L. A. (October 1938), "The Bridge Stabilized Oscillator", Bell System Technical Journal, 17 (4): 574–591, doi:10.1002/j.1538-7305.1938.tb00799.x. Frequency and amplitude stabilization of an oscillator with no tube overloading. Uses tungsten lamp to balance bridge.
- US 2163403, Meacham, Larned A., "Stabilized Oscillator", published 2 July 1937, issued 20 June 1939, assigned to Bell Telephone Laboratories
- Matthys, Robert J. (1992), Crystal Oscillator Circuits (revised ed.), Malabar, Florida: Krieger Publishing Company, pp. 53–57
- Oliver, Bernard M. (April–June 1960), "The Effect of μ-Circuit Non-Linearity on the Amplitude Stability of RC Oscillators" (PDF), Hewlett-Packard Journal, 11 (8–10): 1–8. Shows that amplifier non-linearity is needed for fast amplitude settling of the Wien bridge oscillator.
- Schilling, Donald; Belove, Charles (1968), Electronic Circuits: Discrete and Integrated, McGraw-Hill
- Scott, H. H. (February 1938), "A new type of selective circuit and some applications", Proc. IRE, 26 (2): 226–235, doi:10.1109/JRPROC.1938.228287, S2CID 51674762
- US 2173427, Scott, Hermon Hosner, "Electric Oscillator", published 30 August 1937, issued 19 September 1939, assigned to General Radio Company ; Wien, briged-T, twin-T oscillators
- Sharpe, Ed (n.d.), Hewlett-Packard, The Early Years; Hewlett graduated from Stanford and spent a year doing research; then he goes to MIT to get his masters. Hewlett joins the army, but is discharged in 1936.
- Strauss, Leonard (1970), Wave Generation and Shaping (2nd ed.), McGraw-Hill, ISBN 978-0-07-062161-9
- Terman, Frederick (July 1933), "Resistance-stabilized Oscillators", Electronics, 6: 190
- Terman, Frederick (1935), Measurements in Radio Engineering, New York, NY: McGraw-Hill, pp. 283–289, ASIN B001KZ1IFK, OCLC 180980 (diode limiting)
- Terman, Frederick (1937), Radio Engineering, McGraw-Hill
- Terman, Frederick (1943), Radio Engineers' Handbook, McGraw-Hill
- Wien, M. (1891), "Messung der Inductionsconstanten mit dem "optischen Telephon"" [Measurement of Inductive Constants with the "Optical Telephone"], Annalen der Physik und Chemie (in German), 280 (12): 689–712, Bibcode:1891AnP...280..689W, doi:10.1002/andp.18912801208
- Williams, Jim (June 1990), Bridge Circuits: Marrying Gain and Balance (PDF), Application Note, vol. 43, Linear Technology Inc, pp. 29–33, 43
- Williams, Jim (1991), "Max Wien, Mr. Hewlett, and a Rainy Sunday Afternoon", in Williams, Jim (ed.), Analog Circuit Design, Art, Science, and Personalities, Butterworth Heinemann, pp. 43–58, ISBN 0-7506-9640-0
External links
- Model 200A Audio Oscillator, 1939, HP Virtual Museum.
- Wien Bridge Oscillator, including SPICE simulation. The "Wien bridge oscillator" in the simulation is not a low distortion design with amplitude stabilization; it is a more conventional oscillator with a diode limiter.
- Aigrain, P. R.; Williams, E. M. (January 1948), "Theory of Amplitude-Stabilized Oscillators", Proceedings of the IRE, 36 (1): 16–19, doi:10.1109/JRPROC.1948.230539, S2CID 51640873
- Online Simulator of Wien Bridge Oscillator – Gives online simulation of Wien bridge oscillator.
- Bill Hewlett and his Magic Lamp, Clifton Laboratories
- Terman, F. E.; Buss, R. R.; Hewlett, W. R.; Cahill, F. C. (October 1939), "Some Applications of Negative Feedback with Particular Reference to Laboratory Equipment" (PDF), Proceedings of the IRE, 27 (10): 649–655, doi:10.1109/JRPROC.1939.228752, S2CID 51642790 (Acks Edward L. Ginzton at end of paper.) (Presented 16 June 1938 at 13th Annual Convention, Manuscript received 22 November 1938, abridged 1 August 1939); Meacham presented at 13th Annual Convention on 16 June 1938, too. See BSTJ. Also presented at Pacific Coast Convention, Portland, OR, 11 August 1938.
- Terman et al. (1939, pp. 653–654), §Resistance-stabilized Oscillators Employing Negative Feedback, state "For a discussion of ordinary resistance-stabilized oscillators see pages 283–289 of F. E. Terman, 'Measurements in Radio Engineering,' McGraw-Hill Book Company, New York, N.Y., (1935)." OCLC 180980 ASIN B001KZ1IFK (diode limiting)
- Terman et al. (1939, p. 654) state, "This oscillator somewhat resembles that described by H. H. Scott, in the paper 'A new type of selective circuit and some applications,' Proc. I.R.E., vol 26, pp. 226–236; February, (1938), although differing in a number of respects, such as being provided with amplitude control and having the frequency adjusted by variable condensers rather than variable resistors. The latter feature makes the impedance from a to ground constant as the capacitance is varied to change the frequency, and so greatly simplifies the design of the amplifier circuits."
- US 2319965, Wise, Raymond O., "Variable Frequency Bridge Stabilized Oscillator", published 14 June 1941, issued 25 May 1943, assigned to Bell Telephone Laboratories
- US 2343539, Edson, William A., "Stabilized Oscillator", published 16 January 1942, issued 7 March 1944, assigned to Bell Telephone Laboratories
- http://www.radiomuseum.org/forum/single_pentode_wien_bridge_oscillator.html
- http://www.americanradiohistory.com/Archive-Bell-Laboratories-Record/40s/Bell-Laboratories-Record-1945-12.pdf has Black bio; "Stabilized feedback amplifier" won prize in 1934.
- U.S. patent 2,303,485 Later (31 December 1940) Meacham patent about multi-frequency bridge-stabilized oscillators using series resonant circuits.
| Electronic oscillators | |
|---|---|
| Theory | |
| LC oscillators | |
| RC oscillators | |
| Quartz oscillators | |
| Relaxation oscillators | |
| Other | |


 and
and 

 is the frequency-dependent gain of the op-amp (note, the component names in Schilling have been replaced with the component names in the first figure).
is the frequency-dependent gain of the op-amp (note, the component names in Schilling have been replaced with the component names in the first figure).

 with
with 






 or −2.6180 and −0.38197.
or −2.6180 and −0.38197.