| Revision as of 05:52, 30 April 2024 editJJMC89 bot III (talk | contribs)Bots, Administrators3,690,487 editsm Moving Category:Persian spiritual writers to Category:Persian-language spiritual writers per Misplaced Pages:Categories for discussion/Speedy← Previous edit | Latest revision as of 00:10, 9 January 2025 edit undoAmhmr (talk | contribs)391 editsNo edit summaryTags: Visual edit Mobile edit Mobile web edit | ||
| (53 intermediate revisions by 33 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Persian polymath and poet (1048–1131 |
{{Short description|Persian polymath and poet (1048–1131)}} | ||
| {{Other uses}} | {{Other uses}} | ||
| {{Use dmy dates|date=May 2023}} | {{Use dmy dates|date=May 2023}} | ||
| {{Infobox scholar | {{Infobox scholar | ||
| | native_name = {{Nobold|{{lang|fa|عمر خیّام|rtl=yes}}}} | | native_name = {{Nobold|{{lang|fa|عمر خیّام|rtl=yes}}}} | ||
| | image = File:Hakim Omar Khayam - panoramio.jpg|Hakim Omar Khayam - panoramio | |||
| | image = The Statue of Khayyam in Mashhad (2) (cropped).jpg | |||
| | image_size = |
| image_size = 250px | ||
| | caption = Statue of Khayyam |
| caption = Statue of Khayyam by ] | ||
| | birth_date = 18 May<ref name="Britannica">{{cite web |url=https://www.britannica.com/biography/Omar-Khayyam-Persian-poet-and-astronomer |title=Omar Khayyam: Persian poet and astronomer |last1=Tikkanen|first1=Amy|date=28 February 2023|website=Encyclopaedia Britannica|access-date=5 April 2023}}</ref> |
| birth_date = 18 May 1048<ref name="Britannica">{{cite web |url=https://www.britannica.com/biography/Omar-Khayyam-Persian-poet-and-astronomer |title=Omar Khayyam: Persian poet and astronomer |last1=Tikkanen|first1=Amy|date=28 February 2023|website=Encyclopaedia Britannica|access-date=5 April 2023}}</ref><ref name="NasrRazavi">{{cite book |last1=Nasr |first1=S.H.|last2=Aminrazavi|first2=M.|last3= with the assistance of M. R. Jozi|author1-link=Seyyed Hossein Nasr|author2-link=Mehdi Aminrazavi |title=An Anthology of Philosophy in Persia. Volume I: From Zoroaster to Omar Khayyam |url=https://books.google.com/books?id=O-vWAAAAMAAJ&q=An+Anthology+of+Philosophy+in+Persia.+Volume+I:+From+Zoroaster |date=2008|publisher=I.B. Tauris, in association with The Institute of Ismaili Studies London|location=London & New York|isbn=978-1-84511-541-8}}</ref> | ||
| | birth_place = ], ], ] | | birth_place = ], ], ] | ||
| | death_date = 4 December<ref name="Britannica" /> |
| death_date = 4 December 1131 (aged 83)<ref name="Britannica" /><ref name="NasrRazavi"/> | ||
| | death_place = Nishapur, Khorasan, |
| death_place = Nishapur, Khorasan, Seljuk Iran | ||
| | main_interests = {{cslist|]|]|]|]}} | | main_interests = {{cslist|]|]|]|]}} | ||
| | influences = {{cslist|]|]|]|]}} | | influences = {{cslist|]|]|]|]}} | ||
| Line 17: | Line 17: | ||
| }} | }} | ||
| ''' |
'''Ghiyasoldin Abolfath Omar ebn Ebrahim Khayyam Neyshaburi'''<ref name="Britannica"/><ref>{{Cite book |last1=Dehkhoda|first1=A.A.|author-link=Ali-Akbar Dehkhoda|chapter=Khayyam|title=]|location=Tehran|language=fa|chapter-url=https://vajehyab.com/dehkhoda/%D8%AE%DB%8C%D8%A7%D9%85-7 }}</ref> (18 May 1048 – 4 December 1131), commonly known as '''Omar Khayyam''' ({{langx|fa|عمر خیّام}}),{{efn|{{IPA|fa|oˈmæɾ xæjˈjɒːm|}}; {{IPAc-en|k|aɪ|ˈ|j|ɑː|m|,_|k|aɪ|ˈ|j|æ|m}}}} was a Persian ], known for his contributions to ], ], ], and ].<ref>{{Cite book|last=Levy|first=Reuben|title=The Persian Language|series=Routledge Library Editions: Iran, Volume: XV|location=London & New York|publisher=Routledge|date=2011|orig-date=1951|isbn=978-0-203-83301-8}}</ref>{{rp|94}} He was born in ], the initial ] of the ], and lived during the period of the ], around the time of the ]. | ||
| As a mathematician, he is most notable for his work on the classification and solution of ]s, where he provided geometric |
As a mathematician, he is most notable for his work on the classification and solution of ]s, where he provided a geometric formulation based on the intersection of ]s.<ref name=mactutor>{{MacTutor Biography|date=July 1999|id= Khayyam}}</ref> He also contributed to a deeper understanding of ]'s ].<ref name="Struik">{{cite journal|last1=Struik|first1=D.J.|author-link=Dirk Jan Struik|title=Omar Khayyam, mathematician|journal=The Mathematics Teacher|date=1958|volume=LII|issue=4|pages=280–285|jstor=27955652|url-access=registration|url=https://www.jstor.org/stable/27955652 }}</ref>{{rp|284}} As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the ], a ] with a very precise 33-year ]<ref name="The Cambridge History of Iran">{{cite book|last1=Boyle|first1=J.A.|author1-link=John Andrew Boyle|editor1-last=]|title=]. Volume IV: From the Arab Invasion to the Saljuqs|date=2007 |orig-date=1975|publisher=Cambridge University Press |location=New York |isbn=978-0-521-20093-6|doi=10.1017/CHOL9780521200936.023|pages=658–664|chapter=‘Umar Khayyām: Astronomer, Mathematician and Poet|chapter-url-access=subscription| chapter-url=https://doi.org/10.1017/CHOL9780521200936.023 }}</ref>{{rp|659}} | ||
| {{efn|With an error of one day accumulating over 5,000 years, it was more precise than the ] of 1582, which has an error of one day every 3,330 years.<ref name="The Wine of Wisdom" />{{rp|200}}}} which provided the basis for the ] that is still in use after nearly a millennium. | {{efn|With an error of one day accumulating over 5,000 years, it was more precise than the ] of 1582, which has an error of one day every 3,330 years.<ref name="The Wine of Wisdom" />{{rp|200}}}} which provided the basis for the ] that is still in use after nearly a millennium. | ||
| Line 29: | Line 29: | ||
| ] in ], ]. Some of his rubáiyáts are used as ] decoration on the exterior body of his mausoleum.]] | ] in ], ]. Some of his rubáiyáts are used as ] decoration on the exterior body of his mausoleum.]] | ||
| Khayyam's boyhood was spent in Nishapur,<ref name="The Cambridge History of Iran" />{{rp|659}} a leading metropolis |
Khayyam's boyhood was spent in Nishapur,<ref name="The Cambridge History of Iran" />{{rp|659}} a leading metropolis in the ],<ref name = "Sarton">{{cite journal |last1=Sarton|first1=G.|author-link=George Sarton|title=The Tomb of Omar Khayyâm |journal=Isis|date=1938|volume=XXIX|issue=1|pages=15–19|doi=10.1086/347379|jstor=225920|s2cid=143678233 |url-access=registration|url=https://www.jstor.org/stable/225920 }}</ref>{{rp|15}}<ref name = "FitzGerald">Edward FitzGerald, ''Rubaiyat of Omar Khayyam'', Ed. Christopher Decker, (University of Virginia Press, 1997), xv; "The Seljuq Turks had invaded the province of Khorasan in the 1030s, and the city of Nishapur surrendered to them voluntarily in 1038. Thus Omar Khayyam grew to maturity during the first of the several alien dynasties that would rule Iran until the twentieth century".</ref> which had earlier been a major center of the ].<ref name="The Wine of Wisdom">{{cite book|last1=Aminrazavi|first1=M.|author-link=Mehdi Aminrazavi|title=The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam|date=2007|publisher=Oneworld|location=Oxford|isbn=978-1-85168-355-0}}</ref>{{rp|68}} His full name, as it appears in Arabic sources, was ''Abu’l Fath Omar ibn Ibrahim al-Khayyam''.{{efn|name=ArabicName|In e.g., ],<ref name="The Wine of Wisdom" />{{rp|55}} or ].<ref name="Earliest Account of Khayyam"/>{{rp|463}}<ref name=Bayhaqi/>{{rp|172–175, no. 66}}}} His gifts were recognized by his early tutors who sent him to study under Imam Muwaffaq Nishaburi, the greatest teacher of the Khorasan region who tutored the children of the highest nobility, and Khayyam developed a firm friendship with him through the years.<ref name="The Wine of Wisdom" />{{rp|20}} Khayyam might have met and studied with ], a disciple of ].<ref name="The Wine of Wisdom" />{{rp|20–21}} After studying science, philosophy, mathematics and astronomy at Nishapur, about the year 1068 he traveled to the province of ], where he frequented the renowned library of the ]. In about 1070 he moved to ], where he started to compose his famous '']'' under the patronage of Abu Tahir Abd al-Rahman ibn ʿAlaq, the governor and ] of the city.<ref name=Rosenfeld>{{cite encyclopedia|last1=Rosenfeld|first1=Boris A.|editor1-last=]|title=Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures|date=2016|publisher=Springer–Verlag |location=Dordrecht |isbn=978-94-007-7747-7|doi=10.1007/978-94-007-7747-7_9775|pages=4330b–4332a|edition=3rd|chapter=Umar al-Khayyām|chapter-url-access=subscription|chapter-url=https://doi.org/10.1007/978-94-007-7747-7_9775 }}</ref>{{rp|4330b}} Khayyam was kindly received by the Karakhanid ruler ], who according to Bayhaqi, would "show him the greatest honour, so much so that he would seat beside him on his ]".<ref name="Boyle"/>{{rp|34}}<ref name="The Wine of Wisdom"/>{{rp|47}} | ||
| In 1073–4 peace was concluded with ] ] who had made incursions into Karakhanid dominions. Khayyam entered the service of Malik-Shah in |
In 1073–4 peace was concluded with ] ] who had made incursions into Karakhanid dominions. Khayyam entered the service of Malik-Shah in 1074 when he was invited by the ] ] to meet Malik-Shah in the city of ]. Khayyam was subsequently commissioned to set up an observatory in ] and lead a group of scientists in carrying out precise astronomical observations aimed at the revision of the Persian calendar. The undertaking probably began with the opening of the observatory in 1074 and ended in 1079,<ref name="The Wine of Wisdom"/>{{rp|28–29}} when Omar Khayyam and his colleagues concluded their measurements of the length of the year, reporting it as 365.24219858156 days.<ref name=mactutor/> Given that the length of the year is changing in the sixth decimal place over a person's lifetime, this is outstandingly accurate. For comparison, the length of the year at the end of the 19th century was 365.242196 days, while today it is 365.242190 days. | ||
| After the death of Malik-Shah and his vizier (murdered, it is thought, by the ] ]), Khayyam fell from favor at court, and as a result, he soon set out on his ]. A possible ulterior motive for his pilgrimage reported by ], was a public demonstration of his faith with a view to allaying suspicions of skepticism and confuting the allegations of unorthodoxy (including possible sympathy or adherence to Zoroastrianism) levelled at him by a hostile clergy.<ref name="The Wine of Wisdom" />{{rp|29}}<ref name="The Wine of Wisdom" />{{rp|29}}<ref>{{Cite journal|last=Aminrazavi|first=M.|author-link=Mehdi Aminrazavi|date=2010|title=Review: Omar Khayyam: Poet, Rebel, Astronomer, Hazhir Teimourian|journal=Iranian Studies|volume=XLIII|issue=4|pages=569–571|jstor=23033230|doi=10.1080/00210862.2010.495592|s2cid=162241136|url-access=registration|url=https://www.jstor.org/stable/23033230 }}</ref> He was then invited by the new ] to Marv, possibly to work as a court ].<ref name="Britannica"/> He was later allowed to return to Nishapur owing to his declining health. Upon his return, he seems to have lived the life of a recluse.<ref name="Great Muslim Mathematicians">{{cite book|last1=Mohamed|first1=Mohaini|title=Great Muslim Mathematicians|date=2000|publisher=Penerbit Universiti Teknologi Malaysia|location=Malaysia|isbn=983-52-0157-9}}</ref>{{rp|99}} | After the death of Malik-Shah and his vizier (murdered, it is thought, by the ] ]), Khayyam fell from favor at court, and as a result, he soon set out on his ]. A possible ulterior motive for his pilgrimage reported by ], was a public demonstration of his faith with a view to allaying suspicions of skepticism and confuting the allegations of unorthodoxy (including possible sympathy or adherence to Zoroastrianism) levelled at him by a hostile clergy.<ref name="The Wine of Wisdom" />{{rp|29}}<ref name="The Wine of Wisdom" />{{rp|29}}<ref>{{Cite journal|last=Aminrazavi|first=M.|author-link=Mehdi Aminrazavi|date=2010|title=Review: Omar Khayyam: Poet, Rebel, Astronomer, Hazhir Teimourian|journal=Iranian Studies|volume=XLIII|issue=4|pages=569–571|jstor=23033230|doi=10.1080/00210862.2010.495592|s2cid=162241136|url-access=registration|url=https://www.jstor.org/stable/23033230 }}</ref> He was then invited by the new ] to Marv, possibly to work as a court ].<ref name="Britannica"/> He was later allowed to return to Nishapur owing to his declining health. Upon his return, he seems to have lived the life of a recluse.<ref name="Great Muslim Mathematicians">{{cite book|last1=Mohamed|first1=Mohaini|title=Great Muslim Mathematicians|date=2000|publisher=Penerbit Universiti Teknologi Malaysia|location=Malaysia|isbn=983-52-0157-9}}</ref>{{rp|99}} | ||
| Omar Khayyam died at the age of 83 in his hometown of Nishapur on 4 December 1131, and he is buried in what is now the ]. One of his disciples ] relates the story that sometime during 1112–3 Khayyam was in ] in the company of ] (one of the scientists who had collaborated with him on the Jalali calendar) when he made a prophecy that "my tomb shall be in a spot where the north wind may scatter roses over it".<ref name="Boyle"/>{{rp|36}}<ref name="FitzGerald"/> Four years after his death, Aruzi located his tomb in a cemetery in a then large and well-known quarter of Nishapur on the road to Marv. As it had been foreseen by Khayyam, Aruzi found the tomb situated at the foot of a garden-wall over which pear trees and |
Omar Khayyam died at the age of 83 in his hometown of Nishapur on 4 December 1131, and he is buried in what is now the ]. One of his disciples ] relates the story that sometime during 1112–3 Khayyam was in ] in the company of ] (one of the scientists who had collaborated with him on the Jalali calendar) when he made a prophecy that "my tomb shall be in a spot where the north wind may scatter roses over it".<ref name="Boyle"/>{{rp|36}}<ref name="FitzGerald"/> Four years after his death, Aruzi located his tomb in a cemetery in a then large and well-known quarter of Nishapur on the road to Marv. As it had been foreseen by Khayyam, Aruzi found the tomb situated at the foot of a garden-wall over which pear trees and apricot trees had thrust their heads and dropped their flowers so that his tombstone was hidden beneath them.<ref name="Boyle"/>{{rp|37}} | ||
| ==Mathematics== | ==Mathematics== | ||
| Line 50: | Line 50: | ||
| ] | ] | ||
| ]'s commentaries on Khayyam's treatment of parallels made |
]'s commentaries on Khayyam's treatment of parallels made their way to Europe. ], professor of geometry at ], translated Tusi's commentary into Latin. Jesuit geometer ], whose work (''euclides ab omni naevo vindicatus'', 1733) is generally considered the first step in the eventual development of ], was familiar with the work of Wallis. The American historian of mathematics ] mentions that Saccheri "used the same lemma as the one of Tusi, even lettering the figure in precisely the same way and using the lemma for the same purpose". He further says that "Tusi distinctly states that it is due to Omar Khayyam, and from the text, it seems clear that the latter was his inspirer."<ref name="The Wine of Wisdom" />{{rp|195}}<ref name="Great Muslim Mathematicians" />{{rp|104}}<ref>{{cite journal|last=Smith |first=D.E.|author-link=David Eugene Smith|journal=Scripta Mathematica|title=Euclid, Omar Khayyâm, and Saccheri|pages=5–10|date=1935|volume=III|issue=1|oclc=14156259}}</ref> | ||
| ====Real number concept==== | ====Real number concept==== | ||
| This treatise on Euclid contains another contribution dealing with the ] and with the compounding of ratios. Khayyam discusses the relationship between the concept of ratio and the concept of number and explicitly raises various theoretical difficulties. In particular, he contributes to the theoretical study of the concept of ].<ref>{{cite journal |last1=Vahabzadeh |first1=Bijan|editor-last=Jafar Aghayani-Chawoshi|title=Omar Khayyam and the Concept of Irrational Numbers|journal=Farhang: Quarterly Journal of Humanities and Cultural Studies. Issue Topic: Commemoration of Khayyam (3)|date=2005 |volume=XVIII |issue=53–54 |pages=125–134}}</ref> Displeased with Euclid's definition of equal ratios, he redefined the concept of a number by the use of a |
This treatise on Euclid contains another contribution dealing with the ] and with the compounding of ratios. Khayyam discusses the relationship between the concept of ratio and the concept of number and explicitly raises various theoretical difficulties. In particular, he contributes to the theoretical study of the concept of ].<ref>{{cite journal |last1=Vahabzadeh |first1=Bijan|editor-last=Jafar Aghayani-Chawoshi|title=Omar Khayyam and the Concept of Irrational Numbers|journal=Farhang: Quarterly Journal of Humanities and Cultural Studies. Issue Topic: Commemoration of Khayyam (3)|date=2005 |volume=XVIII |issue=53–54 |pages=125–134}}</ref> Displeased with Euclid's definition of equal ratios, he redefined the concept of a number by the use of a continued fraction as the means of expressing a ratio. ] and Rosenfeld argue that "by placing irrational quantities and numbers on the same operational scale, began a true revolution in the doctrine of number."<ref name=DSB-Khayyam/>{{rp|327b}} Likewise, it was noted by ] that Omar was "on the road to that extension of the number concept which leads to the notion of the ]."<ref name="Struik" />{{rp|284}} | ||
| ===Geometric algebra=== | ===Geometric algebra=== | ||
| Line 65: | Line 65: | ||
| Khayyam seems to have been the first to conceive a general theory of cubic equations,<ref name=mactutor/>{{efn|name=MacTutor-Quote|O'Connor & Robertson (July 1999): ''However, Khayyam himself seems to have been the first to conceive a general theory of cubic equations''.}} and the first to geometrically solve every type of cubic equation, so far as positive roots are concerned.<ref>{{cite journal |last1=Eves|first1=H.|author-link=Howard Eves|title=Omar Khayyam's Solution of Cubic Equations |journal=Mathematics Teacher |date=1958 |volume=LI |issue=4 |pages=285–286 |doi=10.5951/MT.51.4.0285 |jstor=27955653|url-access=registration |url=https://www.jstor.org/stable/27955653 }}</ref> The ''Treatise on Algebra'' contains his work on ]s.<ref>"''Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics''." → {{Citation|first= Lucye|last= Guilbeau|year= 1930|title= The History of the Solution of the Cubic Equation |journal= Mathematics News Letter|volume=V|issue= 4|pages= 8–12|doi=10.2307/3027812 |jstor= 3027812|s2cid= 125245433|url-access=registration|url=https://www.jstor.org/stable/3027812}}</ref>{{rp|9}} It is divided into three parts: (i) equations which can be solved with ], (ii) equations which can be solved by means of ]s, and (iii) equations which involve the ] of the unknown.<ref name=EIr-KhayyamMath/>{{rp|§ 3}} | Khayyam seems to have been the first to conceive a general theory of cubic equations,<ref name=mactutor/>{{efn|name=MacTutor-Quote|O'Connor & Robertson (July 1999): ''However, Khayyam himself seems to have been the first to conceive a general theory of cubic equations''.}} and the first to geometrically solve every type of cubic equation, so far as positive roots are concerned.<ref>{{cite journal |last1=Eves|first1=H.|author-link=Howard Eves|title=Omar Khayyam's Solution of Cubic Equations |journal=Mathematics Teacher |date=1958 |volume=LI |issue=4 |pages=285–286 |doi=10.5951/MT.51.4.0285 |jstor=27955653|url-access=registration |url=https://www.jstor.org/stable/27955653 }}</ref> The ''Treatise on Algebra'' contains his work on ]s.<ref>"''Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics''." → {{Citation|first= Lucye|last= Guilbeau|year= 1930|title= The History of the Solution of the Cubic Equation |journal= Mathematics News Letter|volume=V|issue= 4|pages= 8–12|doi=10.2307/3027812 |jstor= 3027812|s2cid= 125245433|url-access=registration|url=https://www.jstor.org/stable/3027812}}</ref>{{rp|9}} It is divided into three parts: (i) equations which can be solved with ], (ii) equations which can be solved by means of ]s, and (iii) equations which involve the ] of the unknown.<ref name=EIr-KhayyamMath/>{{rp|§ 3}} | ||
| Khayyam produced an exhaustive list of all possible equations involving lines, squares, and cubes.<ref>{{cite journal |last1=Netz |first1=Reviel |title=Archimedes Transformed: The Case of a Result Stating a Maximum for a Cubic Equation |journal=Archive for History of Exact Sciences |date=1999 |volume=LIV |issue=1 |pages=1–47|doi=10.1007/s004070050032|jstor=41134072|s2cid=121468528 |url-access=registration |url=https://www.jstor.org/stable/41134072}}</ref>{{rp|43}} He considered three binomial equations, nine trinomial equations, and seven tetranomial equations.<ref name="Struik" />{{rp|281}} For the first and second degree polynomials, he provided numerical solutions by geometric construction. He concluded that there are fourteen different types of cubics that cannot be reduced to an equation of a lesser degree.<ref name=EI2-Khayyam/>{{rp|831b}}<ref name=DSB-Khayyam/>{{rp|328a}}<ref>{{cite journal |last1=Oaks |first1=Jeffrey A.|title=Khayyām's Scientific Revision of Algebra |journal=Suhayl: International Journal for the History of the Exact and Natural Sciences in Islamic Civilisation |date=2011 |volume=X|pages=47–75|format=PDF|url=https://raco.cat/index.php/Suhayl/article/view/252894 }}</ref>{{rp|49}} For these he could not accomplish the construction of his unknown segment with compass and straight edge. He proceeded to present geometric solutions to all types of cubic equations using the properties of conic sections.<ref name="Struik" />{{rp|281}}<ref name = "Kent&Muraki">{{cite journal|last1=Kent|first1=Deborah A.|author1-link=Deborah Kent|last2=Muraki|first2=David J.|title=A Geometric Solution of a Cubic by Omar Khayyam … in Which Colored Diagrams Are Used Instead of Letters for the Greater Ease of Learners |journal=The American Mathematical Monthly |date=2016 |volume=CXXIII |issue=2 |pages=149–160 |doi=10.4169/amer.math.monthly.123.2.149|jstor=123.2.149|s2cid=124153443 |url-access=registration |url=https://www.jstor.org/stable/10.4169/amer.math.monthly.123.2.149}}</ref>{{rp|157}} The prerequisite lemmas for Khayyam's geometrical proof include ], Prop 13, and ], Prop 12.<ref name="Kent&Muraki" />{{rp|155}} The positive root of a cubic equation was determined as the ] of a point of intersection of two conics, for instance, the intersection of two ]s, or the intersection of a parabola and a circle, ]<ref name="Evelyn Kennedy">{{cite journal|last1=Kennedy|first1=Evelyn|title='Omar Khayyam |journal=The Mathematics Teacher |date=1966 |volume=LIX |issue=3|pages=140–142|doi=10.5951/MT.59.2.0140|jstor=27957296|url-access=registration|url=https://www.jstor.org/stable/27957296 }}</ref>{{rp|141}} However, he acknowledged that the arithmetic problem of these cubics was still unsolved, adding that "possibly someone else will come to know it after us".<ref name="Kent&Muraki" />{{rp|158}} This task remained open until the sixteenth century, where algebraic solution of the cubic equation was found in its generality by ], ], and ] in ].<ref name="Struik" />{{rp|282}} | Khayyam produced an exhaustive list of all possible equations involving lines, squares, and cubes.<ref>{{cite journal |last1=Netz |first1=Reviel |title=Archimedes Transformed: The Case of a Result Stating a Maximum for a Cubic Equation |journal=Archive for History of Exact Sciences |date=1999 |volume=LIV |issue=1 |pages=1–47|doi=10.1007/s004070050032|jstor=41134072|s2cid=121468528 |url-access=registration |url=https://www.jstor.org/stable/41134072}}</ref>{{rp|43}} He considered three binomial equations, nine trinomial equations, and seven tetranomial equations.<ref name="Struik" />{{rp|281}} For the first and second degree polynomials, he provided numerical solutions by geometric construction. He concluded that there are fourteen different types of cubics that cannot be reduced to an equation of a lesser degree.<ref name=EI2-Khayyam/>{{rp|831b}}<ref name=DSB-Khayyam/>{{rp|328a}}<ref>{{cite journal |last1=Oaks |first1=Jeffrey A.|title=Khayyām's Scientific Revision of Algebra |journal=Suhayl: International Journal for the History of the Exact and Natural Sciences in Islamic Civilisation |date=2011 |volume=X|pages=47–75|format=PDF|url=https://raco.cat/index.php/Suhayl/article/view/252894 }}</ref>{{rp|49}} For these he could not accomplish the construction of his unknown segment with compass and straight edge. He proceeded to present geometric solutions to all types of cubic equations using the properties of conic sections.<ref name="Struik" />{{rp|281}}<ref name = "Kent&Muraki">{{cite journal|last1=Kent|first1=Deborah A.|author1-link=Deborah Kent|last2=Muraki|first2=David J.|title=A Geometric Solution of a Cubic by Omar Khayyam … in Which Colored Diagrams Are Used Instead of Letters for the Greater Ease of Learners |journal=The American Mathematical Monthly |date=2016 |volume=CXXIII |issue=2 |pages=149–160 |doi=10.4169/amer.math.monthly.123.2.149|jstor=123.2.149|s2cid=124153443 |url-access=registration |url=https://www.jstor.org/stable/10.4169/amer.math.monthly.123.2.149}}</ref>{{rp|157}} The prerequisite lemmas for Khayyam's geometrical proof include ], Prop 13, and ], Prop 12.<ref name="Kent&Muraki" />{{rp|155}} The positive root of a cubic equation was determined as the ] of a point of intersection of two conics, for instance, the intersection of two ]s, or the intersection of a parabola and a circle, ]<ref name="Evelyn Kennedy">{{cite journal|last1=Kennedy|first1=Evelyn|title='Omar Khayyam |journal=The Mathematics Teacher |date=1966 |volume=LIX |issue=3|pages=140–142|doi=10.5951/MT.59.2.0140|jstor=27957296|url-access=registration|url=https://www.jstor.org/stable/27957296 }}</ref>{{rp|141}} However, he acknowledged that the arithmetic problem of these cubics was still unsolved, adding that "possibly someone else will come to know it after us".<ref name="Kent&Muraki" />{{rp|158}} This task remained open until the sixteenth century, where an algebraic solution of the cubic equation was found in its generality by ], ], and ] in ].<ref name="Struik" />{{rp|282}} | ||
| {{quote box|width=30%|quote=Whoever thinks ] is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and ] are different in appearance. Algebras are geometric facts which are proved by propositions five and six of Book two of ].|source=—Omar Khayyam<ref name=amirmoez>{{cite journal |last1=Amir-Moez |first1=A.R. |title=A Paper of Omar Khayyam |journal=Scripta Mathematica |date=1963 |volume=XXVI |pages=323–337}}</ref>}} | {{quote box|width=30%|quote=Whoever thinks ] is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and ] are different in appearance. Algebras are geometric facts which are proved by propositions five and six of Book two of ].|source=—Omar Khayyam<ref name=amirmoez>{{cite journal |last1=Amir-Moez |first1=A.R. |title=A Paper of Omar Khayyam |journal=Scripta Mathematica |date=1963 |volume=XXVI |pages=323–337}}</ref>}} | ||
| In effect, Khayyam's work is an effort to unify algebra and geometry.<ref name = "Kasir review">{{cite journal |title=Review: The Algebra of Omar Khayyam by Daoud Kasir |journal=The Mathematics Teacher |date=1932 |volume=XXV |issue=4 |pages=238–241|jstor=27951448|url-access=registration |url=https://www.jstor.org/stable/27951448}}</ref>{{rp|241}} This particular geometric solution of cubic equations |
In effect, Khayyam's work is an effort to unify algebra and geometry.<ref name = "Kasir review">{{cite journal |title=Review: The Algebra of Omar Khayyam by Daoud Kasir |journal=The Mathematics Teacher |date=1932 |volume=XXV |issue=4 |pages=238–241|jstor=27951448|url-access=registration |url=https://www.jstor.org/stable/27951448}}</ref>{{rp|241}} This particular geometric solution of cubic equations was further investigated by ] and extended to solving fourth-degree equations.<ref>{{cite journal |last1=Amir-Moez |first1=A. R. |title=Khayyam's Solution of Cubic Equations |journal=Mathematics Magazine |date=1962 |volume=XXXV |issue=5 |pages=269–271|doi=10.2307/2688197|jstor=2688197|url-access=registration |url=https://www.jstor.org/stable/2688197 |quote=This paper contains an extension by ] of Khayyam's method to degree four equations.}}</ref> Although similar methods had appeared sporadically since ], and further developed by the 10th-century mathematician ],<ref>{{Cite book|location=New York |publisher = Springer Science & Business Media| isbn = 978-3-642-51599-6| last = Waerden| first = B.L.|author-link=Bartel Leendert van der Waerden| title = A History of Algebra: From al-Khwārizmī to Emmy Noether| date = 2013}}</ref>{{rp|29}}<ref>{{cite book |last1=Van Brummelen |first1=Glen |editor1-last=Nathan Sidoli |editor2-last=] |title=From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren |date=2014 |publisher=Springer |location=New York|doi=10.1007/978-3-642-36736-6_6 |isbn=978-3-642-36736-6 |pages=101–138 |chapter=A Survey of Research in the Mathematical Sciences in Medieval Islam from 1996 to 2011|chapter-url-access=subscription|chapter-url=https://doi.org/10.1007/978-3-642-36736-6_6 }}</ref>{{rp|110}} Khayyam's work can be considered the first systematic study and the first exact method of solving cubic equations.<ref>{{cite book|last1=Knoebel|first1=Art|last2=Laubenbacher|first2=Reinhard|last3=Lodder| first3=Jerry| date= 2007| title=Mathematical Masterpieces: Further Chronicles by the Explorers|publisher=Springer|isbn=978-0-387-33060-0}}</ref>{{rp|92}} The mathematician ] (1851) who offered translations of Khayyam's algebra into French praised him for his "power of generalization and his rigorously systematic procedure."<ref name = "Whinfield">{{cite book |last1=Whinfield |first1=E.H.|author-link=Edward Henry Whinfield |title=The Quatrains of Omar Khayyam: The Persian Text with an English Verse Translation |date=2000 |publisher=Psychology Press Ltd |location=New York |url=https://archive.org/details/in.ernet.dli.2015.37199/page/n15/mode/2up?view=theater}}</ref>{{rp|10}} | ||
| ===Binomial theorem and extraction of roots=== | ===Binomial theorem and extraction of roots=== | ||
| Line 76: | Line 76: | ||
| {{Quote box|quote=From the ] one has methods for obtaining ] and ]s, methods based on knowledge of individual cases{{snd}}namely the knowledge of the squares of the nine digits 1<sup>2</sup>, 2<sup>2</sup>, 3<sup>2</sup> (etc.) and their respective products, i.e. 2 × 3 etc. We have written a treatise on the proof of the validity of those methods and that they satisfy the conditions. In addition we have increased their types, namely in the form of the determination of the fourth, fifth, sixth roots up to any desired degree. No one preceded us in this and those proofs are purely arithmetic, founded on the arithmetic of '']''.|source = —Omar Khayyam, ''Treatise on Algebra''<ref>{{cite web |last1=O'Connor |first1=John J.|last2=Robertson|first2=E.F.|author2-link=Edmund F. Robertson|title=Muslim Extraction of Roots |url=https://mathshistory.st-andrews.ac.uk/Extras/Muslim_roots/ |website=MacTutor History of Mathematics Archive |publisher=University of St Andrews |date=2006}}</ref>| width = 35%}} | {{Quote box|quote=From the ] one has methods for obtaining ] and ]s, methods based on knowledge of individual cases{{snd}}namely the knowledge of the squares of the nine digits 1<sup>2</sup>, 2<sup>2</sup>, 3<sup>2</sup> (etc.) and their respective products, i.e. 2 × 3 etc. We have written a treatise on the proof of the validity of those methods and that they satisfy the conditions. In addition we have increased their types, namely in the form of the determination of the fourth, fifth, sixth roots up to any desired degree. No one preceded us in this and those proofs are purely arithmetic, founded on the arithmetic of '']''.|source = —Omar Khayyam, ''Treatise on Algebra''<ref>{{cite web |last1=O'Connor |first1=John J.|last2=Robertson|first2=E.F.|author2-link=Edmund F. Robertson|title=Muslim Extraction of Roots |url=https://mathshistory.st-andrews.ac.uk/Extras/Muslim_roots/ |website=MacTutor History of Mathematics Archive |publisher=University of St Andrews |date=2006}}</ref>| width = 35%}} | ||
| In his algebraic treatise, Khayyam alludes to a book he had written on the extraction of the <math>n</math>th root of |
In his algebraic treatise, Khayyam alludes to a book he had written on the extraction of the <math>n</math>th root of natural numbers using a law he had discovered which did not depend on geometric figures.<ref name="Evelyn Kennedy" /> This book was most likely titled the ''Difficulties of Arithmetic'' ({{transliteration|ar|Mushkilāt al-Ḥisāb}}),<ref name=EI2-Khayyam/>{{rp|832a}}<ref name=EIr-KhayyamMath/>{{rp|§ 4}} and is not extant.<ref name=DSB-Khayyam/>{{rp|325b}} Based on the context, some historians of mathematics such as D. J. Struik, believe that Omar must have known the formula for the expansion of the binomial <math>(a+b)^n</math>, where {{math|''n''}} is a positive integer.<ref name="Struik" />{{rp|282}} The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyam was the ] who noticed the importance of a general binomial theorem. The argument supporting the claim that Khayyam had a general binomial theorem is based on his ability to extract roots.<ref>{{cite journal |last1=Coolidge |first1=J.L. |title=The Story of the Binomial Theorem |journal=American Mathematical Monthly |date=1985 |volume=LVI |issue=3 |pages=147–157| doi=10.2307/2305028 |jstor=2305028 |url-access=registration |url=https://www.jstor.org/stable/2305028 }}</ref> One of Khayyam's predecessors, ], had already discovered the triangular arrangement of the coefficients of binomial expansions that Europeans later came to know as ];<ref>{{cite book |last1=Nichols |first1=Susan|title=Al-Karaji: Tenth-Century Mathematician and Engineer |date=2017|publisher=Rosen Publishing |location=New York}}</ref>{{rp|60}} Khayyam popularized this ] in Iran, so that it is now known as Omar Khayyam's triangle.<ref name="Evelyn Kennedy" /> | ||
| ==Astronomy== | ==Astronomy== | ||
| Line 84: | Line 84: | ||
| In 1074–5, Omar Khayyam was commissioned by Sultan Malik-Shah to build an ] and reform the ]. There was a panel of eight scholars working under the direction of Khayyam to make large-scale astronomical observations and revise the astronomical tables.<ref name="Evelyn Kennedy" />{{rp|141}} Recalibrating the calendar fixed the first day of the year at the exact moment of the passing of the Sun's center across ]. This marks the beginning of spring or ], a day in which the Sun enters the first degree of ] before noon.<ref>{{cite arXiv|last1=Akrami|first1=Musa|title=The Development of Iranian Calendar: Historical and Astronomical Foundations|date=11 February 2014|class=physics.hist-ph |eprint=1111.4926v2}}</ref>{{rp|10–11}}<ref>{{cite web |url=https://www.iranicaonline.org/articles/calendars#pt2 |title=Calendars ii. In the Islamic period|last1=Abdollahy|first1=Reza|editor-last=]|date=December 15, 1990|website=]|publisher=Encyclopaedia Iranica Foundation |access-date=21 November 2017}}</ref> The resultant calendar was named in Malik-Shah's honor as the ], and was inaugurated on 15 March 1079.<ref>{{cite journal|last1=Farrell|first1=Charlotte|title=The Ninth-century Renaissance in Astronomy|journal=The Physics Teacher |date=1996|volume=XXXIV|issue=5|pages=268–272|bibcode = 1996PhTea..34..268F|doi=10.1119/1.2344432}}</ref>{{rp|269}} The ] itself was disused after the death of Malik-Shah in 1092.<ref name="The Cambridge History of Iran" />{{rp|659}} | In 1074–5, Omar Khayyam was commissioned by Sultan Malik-Shah to build an ] and reform the ]. There was a panel of eight scholars working under the direction of Khayyam to make large-scale astronomical observations and revise the astronomical tables.<ref name="Evelyn Kennedy" />{{rp|141}} Recalibrating the calendar fixed the first day of the year at the exact moment of the passing of the Sun's center across ]. This marks the beginning of spring or ], a day in which the Sun enters the first degree of ] before noon.<ref>{{cite arXiv|last1=Akrami|first1=Musa|title=The Development of Iranian Calendar: Historical and Astronomical Foundations|date=11 February 2014|class=physics.hist-ph |eprint=1111.4926v2}}</ref>{{rp|10–11}}<ref>{{cite web |url=https://www.iranicaonline.org/articles/calendars#pt2 |title=Calendars ii. In the Islamic period|last1=Abdollahy|first1=Reza|editor-last=]|date=December 15, 1990|website=]|publisher=Encyclopaedia Iranica Foundation |access-date=21 November 2017}}</ref> The resultant calendar was named in Malik-Shah's honor as the ], and was inaugurated on 15 March 1079.<ref>{{cite journal|last1=Farrell|first1=Charlotte|title=The Ninth-century Renaissance in Astronomy|journal=The Physics Teacher |date=1996|volume=XXXIV|issue=5|pages=268–272|bibcode = 1996PhTea..34..268F|doi=10.1119/1.2344432}}</ref>{{rp|269}} The ] itself was disused after the death of Malik-Shah in 1092.<ref name="The Cambridge History of Iran" />{{rp|659}} | ||
| The Jalālī calendar was a true ] where the duration of each month is equal to the time of the passage of the Sun across the corresponding sign of the ]. The calendar reform introduced a unique 33-year ] cycle. As indicated by the works of ], Khayyam's group implemented an intercalation system based on quadrennial and quinquennial ]. Therefore, the calendar consisted of 25 ordinary years that included 365 days, and 8 leap years that included 366 days.<ref>{{cite arXiv|last1=Heydari-Malayeri|first1=M.|title=Concise Review of the Iranian Calendar|date=21 October 2004|eprint=astro-ph/0409620v2}}</ref>{{rp|13}} The calendar remained in use across ] from the 11th to the 20th centuries. In 1911 the Jalali calendar became the official national calendar of ]. In 1925 this calendar was simplified and the names of the months were |
The Jalālī calendar was a true ] where the duration of each month is equal to the time of the passage of the Sun across the corresponding sign of the ]. The calendar reform introduced a unique 33-year ] cycle. As indicated by the works of ], Khayyam's group implemented an intercalation system based on quadrennial and quinquennial ]. Therefore, the calendar consisted of 25 ordinary years that included 365 days, and 8 leap years that included 366 days.<ref>{{cite arXiv|last1=Heydari-Malayeri|first1=M.|title=Concise Review of the Iranian Calendar|date=21 October 2004|eprint=astro-ph/0409620v2}}</ref>{{rp|13}} The calendar remained in use across ] from the 11th to the 20th centuries. In 1911 the Jalali calendar became the official national calendar of ]. In 1925 this calendar was simplified and the names of the months were modernised, resulting in the ]. The Jalali calendar is more accurate than the ] of 1582,<ref name="The Cambridge History of Iran" />{{rp|659}} with an error of one day accumulating over 5,000 years, compared to one day every 3,330 years in the Gregorian calendar.<ref name="The Wine of Wisdom" />{{rp|200}} ] considered it the most perfect calendar ever devised.<ref name="Great Muslim Mathematicians"/>{{rp|101}} | ||
| One of his pupils ] relates that Khayyam apparently did not have a belief in astrology and divination: "I did not observe that he (''scil.'' Omar Khayyam) had any great belief in astrological predictions, nor have I seen or heard of any of the great who had such belief."<ref name="Whinfield" />{{rp|11}} While working for Sultan Sanjar as an astrologer he was asked to predict the weather – a job that he apparently did not do well.<ref name="The Wine of Wisdom" />{{rp|30}} ] explains that the term {{transliteration|ar|‘ilm al-nujūm}}, used in various sources in which references to Khayyam's life and work could be found, has sometimes been incorrectly translated to mean astrology. He adds: "from at least the middle of the tenth century, according to ]'s ''Enumeration of the Sciences'', that this science, {{transliteration|ar|‘ilm al-nujūm}}, was already split into two parts, one dealing with astrology and the other with theoretical mathematical astronomy."<ref>{{cite journal |last1=Saliba|first1=G.|author-link=George Saliba|title=Review: Al-Khayyām Mathématicien, by R. Rashed; B. Vahabzadeh; Omar Khayyam the Mathematician, by R. Rashed; B. Vahabzadeh|journal=Iranian Studies|date=2002|volume=XXXV |issue=1–3|pages=220–225|doi=10.1017/S0021086200003686 |jstor=4311451|url-access=registration|url=https://www.jstor.org/stable/4311451}}</ref>{{rp|224}} | One of his pupils ] relates that Khayyam apparently did not have a belief in astrology and divination: "I did not observe that he (''scil.'' Omar Khayyam) had any great belief in astrological predictions, nor have I seen or heard of any of the great who had such belief."<ref name="Whinfield" />{{rp|11}} While working for Sultan Sanjar as an astrologer he was asked to predict the weather – a job that he apparently did not do well.<ref name="The Wine of Wisdom" />{{rp|30}} ] explains that the term {{transliteration|ar|‘ilm al-nujūm}}, used in various sources in which references to Khayyam's life and work could be found, has sometimes been incorrectly translated to mean astrology. He adds: "from at least the middle of the tenth century, according to ]'s ''Enumeration of the Sciences'', that this science, {{transliteration|ar|‘ilm al-nujūm}}, was already split into two parts, one dealing with astrology and the other with theoretical mathematical astronomy."<ref>{{cite journal |last1=Saliba|first1=G.|author-link=George Saliba|title=Review: Al-Khayyām Mathématicien, by R. Rashed; B. Vahabzadeh; Omar Khayyam the Mathematician, by R. Rashed; B. Vahabzadeh|journal=Iranian Studies|date=2002|volume=XXXV |issue=1–3|pages=220–225|doi=10.1017/S0021086200003686 |jstor=4311451|url-access=registration|url=https://www.jstor.org/stable/4311451}}</ref>{{rp|224}} | ||
| Line 91: | Line 91: | ||
| {{See also|Specific gravity}} | {{See also|Specific gravity}} | ||
| Khayyam has a short treatise devoted to ] (in full title, ''On the Deception of Knowing the Two Quantities of Gold and Silver in a Compound Made of the Two''). For a compound of gold adulterated with silver, he describes a method to measure more exactly the weight per capacity of each element. It involves weighing the compound both in air and in water, since weights are easier to measure exactly than volumes. By repeating the same with both gold and silver one finds exactly how much heavier than water gold, silver and the compound were. This treatise was extensively examined by ] who believed that Khayyam's solution was more accurate and sophisticated than that of ] and ] who also dealt with the subject elsewhere.<ref name="The Wine of Wisdom" />{{rp|198}} | |||
| Another short treatise is concerned with ] in which he discusses the connection between music and arithmetic. Khayyam's contribution was in providing a systematic classification of musical scales, and discussing the mathematical relationship among notes, minor, major and ].<ref name="The Wine of Wisdom" />{{rp|198}} | Another short treatise is concerned with ] in which he discusses the connection between music and arithmetic. Khayyam's contribution was in providing a systematic classification of musical scales, and discussing the mathematical relationship among notes, minor, major and ].<ref name="The Wine of Wisdom" />{{rp|198}} | ||
| Line 98: | Line 98: | ||
| ] calligraphy.]] | ] calligraphy.]] | ||
| The earliest allusion to Omar Khayyam's poetry is from the historian ], a younger contemporary of Khayyam, who explicitly identifies him as both a poet and a scientist ({{transliteration|ar|Kharidat al-qasr}}, 1174).<ref name="The Wine of Wisdom" />{{rp|49}}<ref name="Dashti">Ali Dashti (translated by L. P. Elwell-Sutton), ''In Search of Omar Khayyam'', Routledge Library Editions: Iran (2012)</ref>{{rp|35}} One of the earliest specimens of Omar Khayyam's Rubiyat is from ]. In his work {{transliteration|ar|al-Tanbih ‘ala ba‘d asrar al-maw‘dat fi’l-Qur’an}} ({{circa|1160}}), he quotes one of his poems (corresponding to quatrain LXII of FitzGerald's first edition). ] in his writings ({{transliteration|ar|Mirṣād al-‘Ibad}}, c. 1230) quotes two quatrains, one of which is the same as the one already reported by Razi. An additional quatrain is quoted by the historian ] ({{transliteration|fa|]}}, c. 1226–1283).<ref name="Dashti" />{{rp|36–37}}<ref name="The Wine of Wisdom" />{{rp|92}} In 1340 ] includes thirteen quatrains of Khayyam in his work containing an anthology of the works of famous Persian poets ({{transliteration|ar|Mu’nis al-ahrār}}), two of which have hitherto been known from the older sources.<ref name = "Ross 1927">{{cite journal|last1=Ross|first1=E.D.|author-link=Edward Denison Ross|title='Omar Khayyam |journal=Bulletin of the School of Oriental Studies|date=1927|volume=IV|issue=3 |pages=433–439 |doi=10.1017/S0041977X00102897|jstor=606948|s2cid=246638673|url-access=registration|url=https://www.jstor.org/stable/606948}}</ref>{{rp|434}} A comparatively late manuscript is the ] MS. Ouseley 140, written in ] in 1460, which contains 158 quatrains on 47 folia. The manuscript belonged to ] (1767–1842) and was purchased by the Bodleian Library in 1844. | The earliest allusion to Omar Khayyam's poetry is from the historian ], a younger contemporary of Khayyam, who explicitly identifies him as both a poet and a scientist ({{transliteration|ar|Kharidat al-qasr}}, 1174).<ref name="The Wine of Wisdom" />{{rp|49}}<ref name="Dashti">Ali Dashti (translated by L. P. Elwell-Sutton), ''In Search of Omar Khayyam'', Routledge Library Editions: Iran (2012)</ref>{{rp|35}} One of the earliest specimens of Omar Khayyam's Rubiyat is from ]. In his work {{transliteration|ar|al-Tanbih ‘ala ba‘d asrar al-maw‘dat fi’l-Qur’an}} ({{circa|1160}}), he quotes one of his poems (corresponding to quatrain LXII of FitzGerald's first edition). ] in his writings ({{transliteration|ar|Mirṣād al-‘Ibad}}, c. 1230) quotes two quatrains, one of which is the same as the one already reported by Razi. An additional quatrain is quoted by the historian ] ({{transliteration|fa|]}}, c. 1226–1283).<ref name="Dashti" />{{rp|36–37}}<ref name="The Wine of Wisdom" />{{rp|92}} In 1340 ] includes thirteen quatrains of Khayyam in his work containing an anthology of the works of famous Persian poets ({{transliteration|ar|Mu’nis al-ahrār}}), two of which have hitherto been known from the older sources.<ref name = "Ross 1927">{{cite journal|last1=Ross|first1=E.D.|author-link=Edward Denison Ross|title='Omar Khayyam |journal=Bulletin of the School of Oriental Studies|date=1927|volume=IV|issue=3 |pages=433–439 |doi=10.1017/S0041977X00102897|jstor=606948|s2cid=246638673|url-access=registration|url=https://www.jstor.org/stable/606948}}</ref>{{rp|434}} A comparatively late manuscript is the ] MS. Ouseley 140, written in ] in 1460, which contains 158 quatrains on 47 folia. The manuscript belonged to ] (1767–1842) and was purchased by the Bodleian Library in 1844. | ||
| ] in ], ]]] | ] in ], ]]] | ||
| Line 141: | Line 141: | ||
| ==Reception== | ==Reception== | ||
| ] in 1997, entitled "850th birth anniversary of Omar Khayyam"]] | ] in 1997, entitled "850th birth anniversary of Omar Khayyam"]] | ||
| The various biographical extracts referring to Omar Khayyam describe him as unequalled in scientific knowledge and achievement during his time.{{efn|name=Biographical extracts|E.g., by the author of ''Firdaws al-tawārikh'',<ref name="E.D. Ross"/>{{rp|356}} author of ''Tārikh alfī'',<ref name="E.D. Ross"/>{{rp|358}} and ].<ref name="The Wine of Wisdom" />{{rp|49}}}} Many called him by the epithet ''King of the Wise'' ({{ |
The various biographical extracts referring to Omar Khayyam describe him as unequalled in scientific knowledge and achievement during his time.{{efn|name=Biographical extracts|E.g., by the author of ''Firdaws al-tawārikh'',<ref name="E.D. Ross"/>{{rp|356}} author of ''Tārikh alfī'',<ref name="E.D. Ross"/>{{rp|358}} and ].<ref name="The Wine of Wisdom" />{{rp|49}}}} Many called him by the epithet ''King of the Wise'' ({{langx|ar|ملك الحکماء|Malik al-Ḥukamā | ||
| }}).<ref name="Ross 1927" />{{rp|436}}<ref name="Evelyn Kennedy" />{{rp|141}} ] (d. 1300) esteems him highly as a mathematician, and claims that he may be regarded as "the successor of ] in the various branches of philosophic learning".<ref name="E.D. Ross" />{{rp|352}} ] (d. 1248), even though disagreeing with his views, concedes he was "unrivalled in his knowledge of natural philosophy and astronomy".<ref name="E.D. Ross" />{{rp|355}} Despite being hailed as a poet by a number of biographers, according to ] "it is still possible to argue that Khayyam's status as a poet of the first rank is a comparatively late development."<ref name="The Cambridge History of Iran" />{{rp|663}} | |||
| ] was the first European to call attention to Khayyam and to translate one of his quatrains into Latin (''Historia religionis veterum Persarum eorumque magorum'', 1700).<ref>{{cite journal|last1=Beveridge|first1=H.|author-link=Henry Beveridge (orientalist)|title=Omar Khayyam|journal=Journal of the Royal Asiatic Society|date=1905|volume=XXXVII|issue=3|pages=521–526|doi=10.1017/S0035869X00033530|jstor=25210170|url-access=registration|url=https://www.jstor.org/stable/25210170}}</ref>{{rp|525}} Western interest in Persia grew with the ] movement in the 19th century. ] (1774–1856) translated some of Khayyam's poems into German in 1818, and ] (1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of ]'s '']'' in 1859. FitzGerald's work at first was unsuccessful but was popularised by ] from 1861 onward, and the work came to be greatly admired by the ]. In 1872 FitzGerald had a third edition printed which increased interest in the work in America. By the 1880s, the book was extremely well known throughout the English-speaking world, to the extent of the formation of numerous "Omar Khayyam Clubs" and a "fin de siècle cult of the Rubaiyat".<ref>J. D. Yohannan, ''Persian Poetry in England and America'', 1977.</ref>{{rp|202}} Khayyam's poems have been translated into many languages; many of the more recent ones are more literal than that of FitzGerald.<ref name="Reception">{{cite book|editor1-last=Seyed-Gohrab|editor1-first=A.A.|editor1-link=Asghar Seyed-Gohrab|title=The Great 'Umar Khayyam: A Global Reception of the Rubáiyát|date=2012|publisher=Leiden University Press|location=Leiden|isbn=978-94-0060-079-9|format=PDF|url=https://muse.jhu.edu/book/46345}}</ref> | ] was the first European to call attention to Khayyam and to translate one of his quatrains into Latin (''Historia religionis veterum Persarum eorumque magorum'', 1700).<ref>{{cite journal|last1=Beveridge|first1=H.|author-link=Henry Beveridge (orientalist)|title=Omar Khayyam|journal=Journal of the Royal Asiatic Society|date=1905|volume=XXXVII|issue=3|pages=521–526|doi=10.1017/S0035869X00033530|jstor=25210170|url-access=registration|url=https://www.jstor.org/stable/25210170}}</ref>{{rp|525}} Western interest in Persia grew with the ] movement in the 19th century. ] (1774–1856) translated some of Khayyam's poems into German in 1818, and ] (1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of ]'s '']'' in 1859. FitzGerald's work at first was unsuccessful but was popularised by ] from 1861 onward, and the work came to be greatly admired by the ]. In 1872 FitzGerald had a third edition printed which increased interest in the work in America. By the 1880s, the book was extremely well known throughout the English-speaking world, to the extent of the formation of numerous "Omar Khayyam Clubs" and a "fin de siècle cult of the Rubaiyat".<ref>J. D. Yohannan, ''Persian Poetry in England and America'', 1977.</ref>{{rp|202}} Khayyam's poems have been translated into many languages; many of the more recent ones are more literal than that of FitzGerald.<ref name="Reception">{{cite book|editor1-last=Seyed-Gohrab|editor1-first=A.A.|editor1-link=Asghar Seyed-Gohrab|title=The Great 'Umar Khayyam: A Global Reception of the Rubáiyát|date=2012|publisher=Leiden University Press|location=Leiden|isbn=978-94-0060-079-9|format=PDF|url=https://muse.jhu.edu/book/46345}}</ref> | ||
| FitzGerald's translation was a factor in rekindling interest in Khayyam as a poet even in his native Iran.<ref name ="Simidchieva">Simidchieva, M. (2011). FitzGerald's Rubáiyát and Agnosticism. In A. Poole, C. Van Ruymbeke, & W. Martin (Eds.), FitzGerald's Rubáiyát of Omar Khayyám: Popularity and Neglect. Anthem Press.</ref>{{rp|55–72}} ] in his ''Songs of Khayyam'' (''Taranehha-ye Khayyam'', 1934) reintroduced Khayyam's poetic legacy to modern Iran. Under the ], a new ] of white marble, designed by the architect ], was erected over his tomb. A statue by ] was erected in ], ] in the 1960s, and a bust by the same sculptor was placed near Khayyam's mausoleum in Nishapur. In 2009, the state of Iran donated a ] to the ], inaugurated at ].<ref>{{cite web|url=http://www.unis.unvienna.org/unis/pressrels/2009/unisvic167.html|title=Monument to Be Inaugurated at the Vienna International Centre, 'Scholars Pavilion' donated to International Organizations in Vienna by Iran|last=UNIS}}</ref> In 2016, three statues of Khayyam were unveiled: one at the ], one in Nishapur and one in Florence, Italy.<ref>{{Cite web|url=http://new.tehrantimes.com/news/300191/Khayyam-statue-finally-set-up-at-University-of-Oklahoma|title=Khayyam statue finally set up at University of Oklahoma|website=Tehran Times|access-date=4 April 2016|url-status=dead|archive-url=https://web.archive.org/web/20160405082018/http://new.tehrantimes.com/news/300191/Khayyam-statue-finally-set-up-at-University-of-Oklahoma|archive-date=5 April 2016}}</ref> Over 150 ]s have used the ''Rubaiyat'' as their source of inspiration. The earliest such composer was ].<ref>{{cite web |url=http://www.iranicaonline.org/articles/khayyam-omar-musical-works-rubaiyat |title=Khayyam, Omar xiii. Musical Works Based On The Rubaiyat|last1=Martin|first1=William H.|last2=Mason|first2=Sandra |editor-last=]|date=15 July 2009|website=]|publisher=Encyclopædia Iranica Foundation |access-date=8 October 2023}}</ref> | FitzGerald's translation was a factor in rekindling interest in Khayyam as a poet even in his native Iran.<ref name ="Simidchieva">Simidchieva, M. (2011). FitzGerald's Rubáiyát and Agnosticism. In A. Poole, C. Van Ruymbeke, & W. Martin (Eds.), FitzGerald's Rubáiyát of Omar Khayyám: Popularity and Neglect. Anthem Press.</ref>{{rp|55–72}} ] in his ''Songs of Khayyam'' (''Taranehha-ye Khayyam'', 1934) reintroduced Khayyam's poetic legacy to modern Iran. Under the ], a new ] of white marble, designed by the architect ], was erected over his tomb. A statue by ] was erected in ], ] in the 1960s, and a bust by the same sculptor was placed near Khayyam's mausoleum in Nishapur. In 2009, the state of Iran donated a ] to the ], inaugurated at ].<ref>{{cite web|url=http://www.unis.unvienna.org/unis/pressrels/2009/unisvic167.html|title=Monument to Be Inaugurated at the Vienna International Centre, 'Scholars Pavilion' donated to International Organizations in Vienna by Iran|last=UNIS}}</ref> In 2016, three statues of Khayyam were unveiled: one at the ], one in Nishapur and one in Florence, Italy.<ref>{{Cite web|url=http://new.tehrantimes.com/news/300191/Khayyam-statue-finally-set-up-at-University-of-Oklahoma|title=Khayyam statue finally set up at University of Oklahoma|website=Tehran Times|access-date=4 April 2016|url-status=dead|archive-url=https://web.archive.org/web/20160405082018/http://new.tehrantimes.com/news/300191/Khayyam-statue-finally-set-up-at-University-of-Oklahoma|archive-date=5 April 2016}}</ref> Over 150 ]s have used the ''Rubaiyat'' as their source of inspiration. The earliest such composer was ].<ref>{{cite web |url=http://www.iranicaonline.org/articles/khayyam-omar-musical-works-rubaiyat |title=Khayyam, Omar xiii. Musical Works Based On The Rubaiyat|last1=Martin|first1=William H.|last2=Mason|first2=Sandra |editor-last=]|date=15 July 2009|website=]|publisher=Encyclopædia Iranica Foundation |access-date=8 October 2023}}</ref> | ||
| FitzGerald rendered Khayyam's name as "Tentmaker", and the anglicized name of "Omar the Tentmaker" resonated in English-speaking popular culture for a while. Thus, ] published a novel called ''Omar, the Tentmaker: A Romance of Old Persia'' in 1898. ''Omar the Tentmaker of ]'' is a historical novel by John Smith Clarke, published in 1910. "Omar the Tentmaker" is also the title of a 1914 play by ] in an oriental setting, adapted as a ] in 1922. US General ] was given the nickname "Omar the Tent-Maker" in World War II.<ref>Jeffrey D. Lavoie, ''The Private Life of General Omar N. Bradley'' (2015)</ref>{{rp|13}} | FitzGerald rendered Khayyam's name as "Tentmaker", and the anglicized name of "Omar the Tentmaker" resonated in English-speaking popular culture for a while. Thus, ] published a novel called ''Omar, the Tentmaker: A Romance of Old Persia'' in 1898. ''Omar the Tentmaker of ]'' is a historical novel by John Smith Clarke, published in 1910. "Omar the Tentmaker" is also the title of a 1914 play by ] in an oriental setting, adapted as a ] in 1922. US General ] was given the nickname "Omar the Tent-Maker" in World War II.<ref>Jeffrey D. Lavoie, ''The Private Life of General Omar N. Bradley'' (2015)</ref>{{rp|13}} | ||
| The diverse talents and intellectual pursuits of Khayyam captivated many ] and ] writers throughout history.<ref name="Balıkçıoğlu1">{{cite journal |last1=Balıkçıoğlu |first1=Efe Murat |title=Quatrains of Many Receptions: A Survey of Perceptions of ‘Omar Khayyām in Ottoman and Turkish Translations |journal=Iranian Studies |date=2024 |page=1 |doi=10.1017/irn.2023.72|doi-access=free }}</ref> Scholars often viewed Khayyam as a means to enhance their own poetic prowess and intellectual depth, drawing inspiration and recognition from his writings.<ref name="Balıkçıoğlu1-22">{{cite journal |last1=Balıkçıoğlu |first1=Efe Murat |title=Quatrains of Many Receptions: A Survey of Perceptions of ‘Omar Khayyā m in Ottoman and Turkish Translations |journal=Iranian Studies |date=2024 |pages=1, 22 |doi=10.1017/irn.2023.72|doi-access=free }}</ref> For many Muslim reformers, Khayam's verses provided a counterpoint to the conservative norms prevalent in Islamic societies, allowing room for independent thought and a libertine lifestyle.<ref name="Balıkçıoğlu1-22"/> Figures like ], ], and ] utilized Khayyam's themes to justify their progressive ideologies or to celebrate liberal aspects of their lives, portraying him as a cultural, political, and intellectual role model who demonstrated Islam's compatibility with modern conventions.<ref name="Balıkçıoğlu1-22"/> Similarly, Turkish leftist poets and intellectuals, including ], ], A. Kadir, and Gökçe, appropriated Khayyam to champion their socialist worldview, imbuing his voice with a humanistic tone in the vernacular.<ref name="Balıkçıoğlu1-22"/> Khayyam's resurgence in spoken ] since the 1980s has transformed him into a poet of the people, with numerous books and translations revitalizing his historical significance.<ref name="Balıkçıoğlu1-22"/> Conversely, scholars like Dāniş, Tevfik, and ] advocated for source criticism and the identification of authentic quatrains to discern the genuine Khayyam amidst historical perceptions of his sociocultural image.<ref name="Balıkçıoğlu1-22"/> | |||
| === The Moving Finger quatrain === | === The Moving Finger quatrain === | ||
| Line 161: | Line 164: | ||
| Shall lure it back to cancel half a Line, | Shall lure it back to cancel half a Line, | ||
| Nor all your Tears wash out a Word of it.<ref>FitzGerald, Stanza LXXI, 4th ed.</ref>{{efn|{{lang|fa|بر لوح نشان بودنیها بودهست | Nor all your Tears wash out a Word of it.<ref>FitzGerald, Stanza LXXI, 4th ed.</ref>{{efn|{{lang|fa| | ||
| بر لوح نشان بودنیها بودهست | |||
| پیوسته قلم ز نیک و بد فرسودهست | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | در روز ازل هر آنچه بایست بداد | ||
| ⚫ | غم خوردن و کوشیدن ما بیهودهست}}}}}} | ||
| The title of the novel |
The title of the novel '']'' written by ] and published in 1942 was inspired by this quatrain of the translation of '']'' by ].<ref name="Moving Finger" /> ] also cites this quatrain of Omar Khayyam in one of his speeches, "]":<ref name="Moving Finger" /><ref>{{Cite web|url=http://www2.hawaii.edu/~freeman/courses/phil100/17.%20MLK%20Beyond%20Vietnam.pdf |archive-url=https://ghostarchive.org/archive/20221010/http://www2.hawaii.edu/~freeman/courses/phil100/17.%20MLK%20Beyond%20Vietnam.pdf |archive-date=10 October 2022 |url-status=live|title=17. MLK Beyond Vietnam.pdf (hawaii.edu)}}</ref> | ||
| {{Blockquote|text=“We may cry out desperately for time to pause in her passage, but time is adamant to every plea and rushes on. Over the bleached bones and jumbled residues of numerous civilizations are written the pathetic words, ‘Too late.’ There is an invisible book of life that faithfully records our vigilance or our neglect. Omar Khayyam is right: ‘The moving finger writes, and having writ moves on.’”}} | {{Blockquote|text=“We may cry out desperately for time to pause in her passage, but time is adamant to every plea and rushes on. Over the bleached bones and jumbled residues of numerous civilizations are written the pathetic words, ‘Too late.’ There is an invisible book of life that faithfully records our vigilance or our neglect. Omar Khayyam is right: ‘The moving finger writes, and having writ moves on.’”}} | ||
| Line 245: | Line 253: | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 00:10, 9 January 2025
Persian polymath and poet (1048–1131) For other uses, see Omar Khayyam (disambiguation).
| HakimOmar Khayyam | |
|---|---|
| عمر خیّام | |
 Statue of Khayyam by Abolhassan Sadighi Statue of Khayyam by Abolhassan Sadighi | |
| Born | 18 May 1048 Nishapur, Khorasan, Seljuk Iran |
| Died | 4 December 1131 (aged 83) Nishapur, Khorasan, Seljuk Iran |
| Academic background | |
| Influences | |
| Academic work | |
| Main interests | |
| Influenced | |
Ghiyasoldin Abolfath Omar ebn Ebrahim Khayyam Neyshaburi (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam (Persian: عمر خیّام), was a Persian polymath, known for his contributions to mathematics, astronomy, philosophy, and poetry. He was born in Nishapur, the initial capital of the Seljuk Empire, and lived during the period of the Seljuk dynasty, around the time of the First Crusade.
As a mathematician, he is most notable for his work on the classification and solution of cubic equations, where he provided a geometric formulation based on the intersection of conics. He also contributed to a deeper understanding of Euclid's parallel axiom. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar, a solar calendar with a very precise 33-year intercalation cycle which provided the basis for the Persian calendar that is still in use after nearly a millennium.
There is a tradition of attributing poetry to Omar Khayyam, written in the form of quatrains (rubāʿiyāt رباعیات). This poetry became widely known to the English-reading world in a translation by Edward FitzGerald (Rubaiyat of Omar Khayyam, 1859), which enjoyed great success in the Orientalism of the fin de siècle.
Life
Omar Khayyam was born in Nishapur—a metropolis in Khorasan province, of Persian stock, in 1048. In medieval Persian texts he is usually simply called Omar Khayyam. Although open to doubt, it has often been assumed that his forebears followed the trade of tent-making, since Khayyam means 'tent-maker' in Arabic. The historian Bayhaqi, who was personally acquainted with Khayyam, provides the full details of his horoscope: "he was Gemini, the sun and Mercury being in the ascendant". This was used by modern scholars to establish his date of birth as 18 May 1048.

Khayyam's boyhood was spent in Nishapur, a leading metropolis in the Seljuk Empire, which had earlier been a major center of the Zoroastrian religion. His full name, as it appears in Arabic sources, was Abu’l Fath Omar ibn Ibrahim al-Khayyam. His gifts were recognized by his early tutors who sent him to study under Imam Muwaffaq Nishaburi, the greatest teacher of the Khorasan region who tutored the children of the highest nobility, and Khayyam developed a firm friendship with him through the years. Khayyam might have met and studied with Bahmanyar, a disciple of Avicenna. After studying science, philosophy, mathematics and astronomy at Nishapur, about the year 1068 he traveled to the province of Bukhara, where he frequented the renowned library of the Ark. In about 1070 he moved to Samarkand, where he started to compose his famous Treatise on Algebra under the patronage of Abu Tahir Abd al-Rahman ibn ʿAlaq, the governor and chief judge of the city. Khayyam was kindly received by the Karakhanid ruler Shams al-Mulk Nasr, who according to Bayhaqi, would "show him the greatest honour, so much so that he would seat beside him on his throne".
In 1073–4 peace was concluded with Sultan Malik-Shah I who had made incursions into Karakhanid dominions. Khayyam entered the service of Malik-Shah in 1074 when he was invited by the Grand Vizier Nizam al-Mulk to meet Malik-Shah in the city of Marv. Khayyam was subsequently commissioned to set up an observatory in Isfahan and lead a group of scientists in carrying out precise astronomical observations aimed at the revision of the Persian calendar. The undertaking probably began with the opening of the observatory in 1074 and ended in 1079, when Omar Khayyam and his colleagues concluded their measurements of the length of the year, reporting it as 365.24219858156 days. Given that the length of the year is changing in the sixth decimal place over a person's lifetime, this is outstandingly accurate. For comparison, the length of the year at the end of the 19th century was 365.242196 days, while today it is 365.242190 days.
After the death of Malik-Shah and his vizier (murdered, it is thought, by the Ismaili order of Assassins), Khayyam fell from favor at court, and as a result, he soon set out on his pilgrimage to Mecca. A possible ulterior motive for his pilgrimage reported by Al-Qifti, was a public demonstration of his faith with a view to allaying suspicions of skepticism and confuting the allegations of unorthodoxy (including possible sympathy or adherence to Zoroastrianism) levelled at him by a hostile clergy. He was then invited by the new Sultan Sanjar to Marv, possibly to work as a court astrologer. He was later allowed to return to Nishapur owing to his declining health. Upon his return, he seems to have lived the life of a recluse.
Omar Khayyam died at the age of 83 in his hometown of Nishapur on 4 December 1131, and he is buried in what is now the Mausoleum of Omar Khayyam. One of his disciples Nizami Aruzi relates the story that sometime during 1112–3 Khayyam was in Balkh in the company of Isfizari (one of the scientists who had collaborated with him on the Jalali calendar) when he made a prophecy that "my tomb shall be in a spot where the north wind may scatter roses over it". Four years after his death, Aruzi located his tomb in a cemetery in a then large and well-known quarter of Nishapur on the road to Marv. As it had been foreseen by Khayyam, Aruzi found the tomb situated at the foot of a garden-wall over which pear trees and apricot trees had thrust their heads and dropped their flowers so that his tombstone was hidden beneath them.
Mathematics
Khayyam was famous during his life as a mathematician. His surviving mathematical works include (i) Commentary on the Difficulties Concerning the Postulates of Euclid's Elements (Risāla fī Sharḥ mā Ashkal min Muṣādarāt Kitāb Uqlīdis), completed in December 1077, (ii) Treatise On the Division of a Quadrant of a Circle (Risālah fī Qismah Rub‘ al-Dā’irah), undated but completed prior to the Treatise on Algebra, and (iii) Treatise on Algebra (Risālah fi al-Jabr wa'l-Muqābala), most likely completed in 1079. He furthermore wrote a treatise on the binomial theorem and extracting the n root of natural numbers, which has been lost.
Theory of parallels
See also: Non-Euclidean geometry § History, and Parallel postulate § HistoryPart of Khayyam's Commentary on the Difficulties Concerning the Postulates of Euclid's Elements deals with the parallel axiom. The treatise of Khayyam can be considered the first treatment of the axiom not based on petitio principii, but on a more intuitive postulate. Khayyam refutes the previous attempts by other mathematicians to prove the proposition, mainly on grounds that each of them had postulated something that was by no means easier to admit than the Fifth Postulate itself. Drawing upon Aristotle's views, he rejects the usage of movement in geometry and therefore dismisses the different attempt by Ibn al-Haytham. Unsatisfied with the failure of mathematicians to prove Euclid's statement from his other postulates, Khayyam tried to connect the axiom with the Fourth Postulate, which states that all right angles are equal to one another.
Khayyam was the first to consider the three distinct cases of acute, obtuse, and right angle for the summit angles of a Khayyam-Saccheri quadrilateral. After proving a number of theorems about them, he showed that Postulate V follows from the right angle hypothesis, and refuted the obtuse and acute cases as self-contradictory. His elaborate attempt to prove the parallel postulate was significant for the further development of geometry, as it clearly shows the possibility of non-Euclidean geometries. The hypotheses of acute, obtuse, and right angles are now known to lead respectively to the non-Euclidean hyperbolic geometry of Gauss-Bolyai-Lobachevsky, to that of Riemannian geometry, and to Euclidean geometry.

Tusi's commentaries on Khayyam's treatment of parallels made their way to Europe. John Wallis, professor of geometry at Oxford, translated Tusi's commentary into Latin. Jesuit geometer Girolamo Saccheri, whose work (euclides ab omni naevo vindicatus, 1733) is generally considered the first step in the eventual development of non-Euclidean geometry, was familiar with the work of Wallis. The American historian of mathematics David Eugene Smith mentions that Saccheri "used the same lemma as the one of Tusi, even lettering the figure in precisely the same way and using the lemma for the same purpose". He further says that "Tusi distinctly states that it is due to Omar Khayyam, and from the text, it seems clear that the latter was his inspirer."
Real number concept
This treatise on Euclid contains another contribution dealing with the theory of proportions and with the compounding of ratios. Khayyam discusses the relationship between the concept of ratio and the concept of number and explicitly raises various theoretical difficulties. In particular, he contributes to the theoretical study of the concept of irrational number. Displeased with Euclid's definition of equal ratios, he redefined the concept of a number by the use of a continued fraction as the means of expressing a ratio. Youschkevitch and Rosenfeld argue that "by placing irrational quantities and numbers on the same operational scale, began a true revolution in the doctrine of number." Likewise, it was noted by D. J. Struik that Omar was "on the road to that extension of the number concept which leads to the notion of the real number."
Geometric algebra

Rashed and Vahabzadeh (2000) have argued that because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered the precursor of Descartes in the invention of analytic geometry. In the Treatise on the Division of a Quadrant of a Circle Khayyam applied algebra to geometry. In this work, he devoted himself mainly to investigating whether it is possible to divide a circular quadrant into two parts such that the line segments projected from the dividing point to the perpendicular diameters of the circle form a specific ratio. His solution, in turn, employed several curve constructions that led to equations containing cubic and quadratic terms.
Solution of cubic equations
Khayyam seems to have been the first to conceive a general theory of cubic equations, and the first to geometrically solve every type of cubic equation, so far as positive roots are concerned. The Treatise on Algebra contains his work on cubic equations. It is divided into three parts: (i) equations which can be solved with compass and straight edge, (ii) equations which can be solved by means of conic sections, and (iii) equations which involve the inverse of the unknown.
Khayyam produced an exhaustive list of all possible equations involving lines, squares, and cubes. He considered three binomial equations, nine trinomial equations, and seven tetranomial equations. For the first and second degree polynomials, he provided numerical solutions by geometric construction. He concluded that there are fourteen different types of cubics that cannot be reduced to an equation of a lesser degree. For these he could not accomplish the construction of his unknown segment with compass and straight edge. He proceeded to present geometric solutions to all types of cubic equations using the properties of conic sections. The prerequisite lemmas for Khayyam's geometrical proof include Euclid VI, Prop 13, and Apollonius II, Prop 12. The positive root of a cubic equation was determined as the abscissa of a point of intersection of two conics, for instance, the intersection of two parabolas, or the intersection of a parabola and a circle, etc. However, he acknowledged that the arithmetic problem of these cubics was still unsolved, adding that "possibly someone else will come to know it after us". This task remained open until the sixteenth century, where an algebraic solution of the cubic equation was found in its generality by Cardano, Del Ferro, and Tartaglia in Renaissance Italy.
—Omar KhayyamWhoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved by propositions five and six of Book two of Elements.
In effect, Khayyam's work is an effort to unify algebra and geometry. This particular geometric solution of cubic equations was further investigated by M. Hachtroudi and extended to solving fourth-degree equations. Although similar methods had appeared sporadically since Menaechmus, and further developed by the 10th-century mathematician Abu al-Jud, Khayyam's work can be considered the first systematic study and the first exact method of solving cubic equations. The mathematician Woepcke (1851) who offered translations of Khayyam's algebra into French praised him for his "power of generalization and his rigorously systematic procedure."
Binomial theorem and extraction of roots
See also: Binomial theorem § History—Omar Khayyam, Treatise on AlgebraFrom the Indians one has methods for obtaining square and cube roots, methods based on knowledge of individual cases – namely the knowledge of the squares of the nine digits 1, 2, 3 (etc.) and their respective products, i.e. 2 × 3 etc. We have written a treatise on the proof of the validity of those methods and that they satisfy the conditions. In addition we have increased their types, namely in the form of the determination of the fourth, fifth, sixth roots up to any desired degree. No one preceded us in this and those proofs are purely arithmetic, founded on the arithmetic of The Elements.
In his algebraic treatise, Khayyam alludes to a book he had written on the extraction of the th root of natural numbers using a law he had discovered which did not depend on geometric figures. This book was most likely titled the Difficulties of Arithmetic (Mushkilāt al-Ḥisāb), and is not extant. Based on the context, some historians of mathematics such as D. J. Struik, believe that Omar must have known the formula for the expansion of the binomial , where n is a positive integer. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyam was the mathematician who noticed the importance of a general binomial theorem. The argument supporting the claim that Khayyam had a general binomial theorem is based on his ability to extract roots. One of Khayyam's predecessors, al-Karaji, had already discovered the triangular arrangement of the coefficients of binomial expansions that Europeans later came to know as Pascal's triangle; Khayyam popularized this triangular array in Iran, so that it is now known as Omar Khayyam's triangle.
Astronomy
Main article: Jalali calendar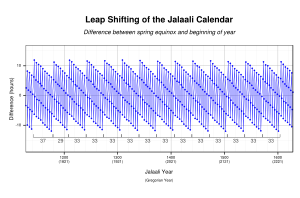
In 1074–5, Omar Khayyam was commissioned by Sultan Malik-Shah to build an observatory at Isfahan and reform the Persian calendar. There was a panel of eight scholars working under the direction of Khayyam to make large-scale astronomical observations and revise the astronomical tables. Recalibrating the calendar fixed the first day of the year at the exact moment of the passing of the Sun's center across vernal equinox. This marks the beginning of spring or Nowrūz, a day in which the Sun enters the first degree of Aries before noon. The resultant calendar was named in Malik-Shah's honor as the Jalālī calendar, and was inaugurated on 15 March 1079. The observatory itself was disused after the death of Malik-Shah in 1092.
The Jalālī calendar was a true solar calendar where the duration of each month is equal to the time of the passage of the Sun across the corresponding sign of the Zodiac. The calendar reform introduced a unique 33-year intercalation cycle. As indicated by the works of Khazini, Khayyam's group implemented an intercalation system based on quadrennial and quinquennial leap years. Therefore, the calendar consisted of 25 ordinary years that included 365 days, and 8 leap years that included 366 days. The calendar remained in use across Greater Iran from the 11th to the 20th centuries. In 1911 the Jalali calendar became the official national calendar of Qajar Iran. In 1925 this calendar was simplified and the names of the months were modernised, resulting in the modern Iranian calendar. The Jalali calendar is more accurate than the Gregorian calendar of 1582, with an error of one day accumulating over 5,000 years, compared to one day every 3,330 years in the Gregorian calendar. Moritz Cantor considered it the most perfect calendar ever devised.
One of his pupils Nizami Aruzi of Samarcand relates that Khayyam apparently did not have a belief in astrology and divination: "I did not observe that he (scil. Omar Khayyam) had any great belief in astrological predictions, nor have I seen or heard of any of the great who had such belief." While working for Sultan Sanjar as an astrologer he was asked to predict the weather – a job that he apparently did not do well. George Saliba explains that the term ‘ilm al-nujūm, used in various sources in which references to Khayyam's life and work could be found, has sometimes been incorrectly translated to mean astrology. He adds: "from at least the middle of the tenth century, according to Farabi's Enumeration of the Sciences, that this science, ‘ilm al-nujūm, was already split into two parts, one dealing with astrology and the other with theoretical mathematical astronomy."
Other works
See also: Specific gravityKhayyam has a short treatise devoted to Archimedes' principle (in full title, On the Deception of Knowing the Two Quantities of Gold and Silver in a Compound Made of the Two). For a compound of gold adulterated with silver, he describes a method to measure more exactly the weight per capacity of each element. It involves weighing the compound both in air and in water, since weights are easier to measure exactly than volumes. By repeating the same with both gold and silver one finds exactly how much heavier than water gold, silver and the compound were. This treatise was extensively examined by Eilhard Wiedemann who believed that Khayyam's solution was more accurate and sophisticated than that of Khazini and Al-Nayrizi who also dealt with the subject elsewhere.
Another short treatise is concerned with music theory in which he discusses the connection between music and arithmetic. Khayyam's contribution was in providing a systematic classification of musical scales, and discussing the mathematical relationship among notes, minor, major and tetrachords.
Poetry

The earliest allusion to Omar Khayyam's poetry is from the historian Imad al-Din al-Isfahani, a younger contemporary of Khayyam, who explicitly identifies him as both a poet and a scientist (Kharidat al-qasr, 1174). One of the earliest specimens of Omar Khayyam's Rubiyat is from Fakhr al-Din Razi. In his work al-Tanbih ‘ala ba‘d asrar al-maw‘dat fi’l-Qur’an (c. 1160), he quotes one of his poems (corresponding to quatrain LXII of FitzGerald's first edition). Daya in his writings (Mirṣād al-‘Ibad, c. 1230) quotes two quatrains, one of which is the same as the one already reported by Razi. An additional quatrain is quoted by the historian Juvayni (Tarikh-i Jahangushay, c. 1226–1283). In 1340 Jajarmi includes thirteen quatrains of Khayyam in his work containing an anthology of the works of famous Persian poets (Mu’nis al-ahrār), two of which have hitherto been known from the older sources. A comparatively late manuscript is the Bodleian MS. Ouseley 140, written in Shiraz in 1460, which contains 158 quatrains on 47 folia. The manuscript belonged to William Ouseley (1767–1842) and was purchased by the Bodleian Library in 1844.

There are occasional quotes of verses attributed to Khayyam in texts attributed to authors of the 13th and 14th centuries, but these are of doubtful authenticity, so that skeptical scholars point out that the entire tradition may be pseudepigraphic. Hans Heinrich Schaeder in 1934 commented that the name of Omar Khayyam "is to be struck out from the history of Persian literature" due to the lack of any material that could confidently be attributed to him. De Blois presents a bibliography of the manuscript tradition, concluding pessimistically that the situation has not changed significantly since Schaeder's time.
Five of the quatrains later attributed to Omar Khayyam are found as early as 30 years after his death, quoted in Sindbad-Nameh. While this establishes that these specific verses were in circulation in Omar's time or shortly later, it does not imply that the verses must be his. De Blois concludes that at the least the process of attributing poetry to Omar Khayyam appears to have begun already in the 13th century. Edward Granville Browne (1906) notes the difficulty of disentangling authentic from spurious quatrains: "while it is certain that Khayyam wrote many quatrains, it is hardly possible, save in a few exceptional cases, to assert positively that he wrote any of those ascribed to him".
In addition to the Persian quatrains, there are twenty-five Arabic poems attributed to Khayyam which are attested by historians such as al-Isfahani, Shahrazuri (Nuzhat al-Arwah, c. 1201–1211), Qifti (Tārikh al-hukamā, 1255), and Hamdallah Mustawfi (Tarikh-i guzida, 1339).
Boyle emphasized that there are a number of other Persian scholars who occasionally wrote quatrains, including Avicenna, Ghazali, and Tusi. They conclude that it is also possible that for Khayyam poetry was an amusement of his leisure hours: "these brief poems seem often to have been the work of scholars and scientists who composed them, perhaps, in moments of relaxation to edify or amuse the inner circle of their disciples".
The poetry attributed to Omar Khayyam has contributed greatly to his popular fame in the modern period as a direct result of the extreme popularity of the translation of such verses into English by Edward FitzGerald (1859). FitzGerald's Rubaiyat of Omar Khayyam contains loose translations of quatrains from the Bodleian manuscript. It enjoyed such success in the fin de siècle period that a bibliography compiled in 1929 listed more than 300 separate editions, and many more have been published since.
Philosophy
Khayyam considered himself intellectually to be a student of Avicenna. According to Al-Bayhaqi, he was reading the metaphysics in Avicenna's the Book of Healing before he died. There are six philosophical papers believed to have been written by Khayyam. One of them, On existence (Fi’l-wujūd), was written originally in Persian and deals with the subject of existence and its relationship to universals. Another paper, titled The necessity of contradiction in the world, determinism and subsistence (Darurat al-tadād fi’l-‘ālam wa’l-jabr wa’l-baqā’), is written in Arabic and deals with free will and determinism. The titles of his other works are On being and necessity (Risālah fī’l-kawn wa’l-taklīf), The Treatise on Transcendence in Existence (al-Risālah al-ulā fi’l-wujūd), On the knowledge of the universal principles of existence (Risālah dar ‘ilm kulliyāt-i wujūd), and Abridgement concerning natural phenomena (Mukhtasar fi’l-Tabi‘iyyāt).
Khayyam himself once said:
We are the victims of an age when men of science are discredited, and only a few remain who are capable of engaging in scientific research. Our philosophers spend all their time in mixing true with false and are interested in nothing but outward show; such little learning as they have they extend on material ends. When they see a man sincere and unremitting in his search for the truth, one who will have nothing to do with falsehood and pretence, they mock and despise him.
Religious views
A literal reading of Khayyam's quatrains leads to the interpretation of his philosophic attitude toward life as a combination of pessimism, nihilism, Epicureanism, fatalism, and agnosticism. This view is taken by Iranologists such as Arthur Christensen, Hans Heinrich Schaeder, John Andrew Boyle, Edward Denison Ross, Edward Henry Whinfield and George Sarton. Conversely, the Khayyamic quatrains have also been described as mystical Sufi poetry. In addition to his Persian quatrains, J. C. E. Bowen mentions that Khayyam's Arabic poems also "express a pessimistic viewpoint which is entirely consonant with the outlook of the deeply thoughtful rationalist philosopher that Khayyam is known historically to have been." Edward FitzGerald emphasized the religious skepticism he found in Khayyam. In his preface to the Rubáiyát he claimed that he "was hated and dreaded by the Sufis", and denied any pretense at divine allegory: "his Wine is the veritable Juice of the Grape: his Tavern, where it was to be had: his Saki, the Flesh and Blood that poured it out for him." Sadegh Hedayat is one of the most notable proponents of Khayyam's philosophy as agnostic skepticism, and according to Jan Rypka (1934), he even considered Khayyam an atheist. Hedayat (1923) states that "while Khayyam believes in the transmutation and transformation of the human body, he does not believe in a separate soul; if we are lucky, our bodily particles would be used in the making of a jug of wine." Omar Khayyam's poetry has been cited in the context of New Atheism, such as in The Portable Atheist by Christopher Hitchens.
Al-Qifti (c. 1172–1248) appears to confirm this view of Khayyam's philosophy. In his work The History of Learned Men he reports that Khayyam's poems were only outwardly in the Sufi style, but were written with an anti-religious agenda. He also mentions that he was at one point indicted for impiety, but went on a pilgrimage to prove he was pious. The report has it that upon returning to his native city he concealed his deepest convictions and practised a strictly religious life, going morning and evening to the place of worship. Khayyam on the Koran (quote 84):
The Koran! well, come put me to the test, Lovely old book in hideous error drest, Believe me, I can quote the Koran too, The unbeliever knows his Koran best. And do you think that unto such as you, A maggot-minded, starved, fanatic crew, God gave the Secret, and denied it me? Well, well, what matters it! believe that too.
Look not above, there is no answer there; Pray not, for no one listens to your prayer; Near is as near to God as any Far, And Here is just the same deceit as There.
Men talk of heaven,—there is no heaven but here; Men talk of hell,—there is no hell but here; Men of hereafters talk, and future lives, O love, there is no other life—but here.
An account of him, written in the thirteenth century, shows him as "versed in all the wisdom of the Greeks," and as wont to insist on the necessity of studying science on Greek lines. Of his prose works, two, which were stand authority, dealt respectively with precious stones and climatology. Beyond question the poet-astronomer was undevout; and his astronomy doubtless helped to make him so. One contemporary writes: "I did not observe that he had any great belief in astrological predictions; nor have I seen or heard of any of the great (scientists) who had such belief. He gave his adherence to no religious sect. Agnosticism, not faith, is the keynote of his works. Among the sects he saw everywhere strife and hatred in which he could have no part...."
Persian novelist Sadegh Hedayat says Khayyám from "his youth to his death remained a materialist, pessimist, agnostic. Khayyam looked at all religions questions with a skeptical eye", continues Hedayat, "and hated the fanaticism, narrow-mindedness, and the spirit of vengeance of the mullas, the so-called religious scholars."
In the context of a piece entitled On the Knowledge of the Principles of Existence, Khayyam endorses the Sufi path. Csillik suggests the possibility that Omar Khayyam could see in Sufism an ally against orthodox religiosity. Other commentators do not accept that Khayyam's poetry has an anti-religious agenda and interpret his references to wine and drunkenness in the conventional metaphorical sense common in Sufism. The French translator J. B. Nicolas held that Khayyam's constant exhortations to drink wine should not be taken literally, but should be regarded rather in the light of Sufi thought where rapturous intoxication by "wine" is to be understood as a metaphor for the enlightened state or divine rapture of baqaa. The view of Omar Khayyam as a Sufi was defended by Bjerregaard, Idries Shah, and Dougan who attributes the reputation of hedonism to the failings of FitzGerald's translation, arguing that Khayyam's poetry is to be understood as "deeply esoteric". On the other hand, Iranian experts such as Mohammad Ali Foroughi and Mojtaba Minovi rejected the hypothesis that Omar Khayyam was a Sufi. Foroughi stated that Khayyam's ideas may have been consistent with that of Sufis at times but there is no evidence that he was formally a Sufi. Aminrazavi states that "Sufi interpretation of Khayyam is possible only by reading into his Rubāʿīyyāt extensively and by stretching the content to fit the classical Sufi doctrine.". Furthermore, Boyle emphasizes that Khayyam was intensely disliked by a number of celebrated Sufi mystics who belonged to the same century. This includes Shams Tabrizi (spiritual guide of Rumi), Najm al-Din Daya who described Omar Khayyam as "an unhappy philosopher, atheist, and materialist", and Attar who regarded him not as a fellow-mystic but a free-thinking scientist who awaited punishments hereafter.
Seyyed Hossein Nasr argues that it is "reductive" to use a literal interpretation of his verses (many of which are of uncertain authenticity to begin with) to establish Omar Khayyam's philosophy. Instead, he adduces Khayyam's interpretive translation of Avicenna's treatise Discourse on Unity (al-Khutbat al-Tawhīd), where he expresses orthodox views on Divine Unity in agreement with the author. The prose works believed to be Khayyam's are written in the Peripatetic style and are explicitly theistic, dealing with subjects such as the existence of God and theodicy. As noted by Bowen these works indicate his involvement in the problems of metaphysics rather than in the subtleties of Sufism. As evidence of Khayyam's faith and/or conformity to Islamic customs, Aminrazavi mentions that in his treatises he offers salutations and prayers, praising God and Muhammad. In most biographical extracts, he is referred to with religious honorifics such as Imām, The Patron of Faith (Ghīyāth al-Dīn), and The Evidence of Truth (Hujjat al-Haqq). He also notes that biographers who praise his religiosity generally avoid making reference to his poetry, while the ones who mention his poetry often do not praise his religious character. For instance, Al-Bayhaqi's account, which antedates by some years other biographical notices, speaks of Omar as a very pious man who professed orthodox views down to his last hour.
On the basis of all the existing textual and biographical evidence, the question remains somewhat open, and as a result Khayyam has received sharply conflicting appreciations and criticisms.
Reception

The various biographical extracts referring to Omar Khayyam describe him as unequalled in scientific knowledge and achievement during his time. Many called him by the epithet King of the Wise (Arabic: ملك الحکماء, romanized: Malik al-Ḥukamā). Shahrazuri (d. 1300) esteems him highly as a mathematician, and claims that he may be regarded as "the successor of Avicenna in the various branches of philosophic learning". Al-Qifti (d. 1248), even though disagreeing with his views, concedes he was "unrivalled in his knowledge of natural philosophy and astronomy". Despite being hailed as a poet by a number of biographers, according to John Andrew Boyle "it is still possible to argue that Khayyam's status as a poet of the first rank is a comparatively late development."
Thomas Hyde was the first European to call attention to Khayyam and to translate one of his quatrains into Latin (Historia religionis veterum Persarum eorumque magorum, 1700). Western interest in Persia grew with the Orientalism movement in the 19th century. Joseph von Hammer-Purgstall (1774–1856) translated some of Khayyam's poems into German in 1818, and Gore Ouseley (1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of Edward FitzGerald's Rubaiyat of Omar Khayyam in 1859. FitzGerald's work at first was unsuccessful but was popularised by Whitley Stokes from 1861 onward, and the work came to be greatly admired by the Pre-Raphaelites. In 1872 FitzGerald had a third edition printed which increased interest in the work in America. By the 1880s, the book was extremely well known throughout the English-speaking world, to the extent of the formation of numerous "Omar Khayyam Clubs" and a "fin de siècle cult of the Rubaiyat". Khayyam's poems have been translated into many languages; many of the more recent ones are more literal than that of FitzGerald.
FitzGerald's translation was a factor in rekindling interest in Khayyam as a poet even in his native Iran. Sadegh Hedayat in his Songs of Khayyam (Taranehha-ye Khayyam, 1934) reintroduced Khayyam's poetic legacy to modern Iran. Under the Pahlavi dynasty, a new monument of white marble, designed by the architect Houshang Seyhoun, was erected over his tomb. A statue by Abolhassan Sadighi was erected in Laleh Park, Tehran in the 1960s, and a bust by the same sculptor was placed near Khayyam's mausoleum in Nishapur. In 2009, the state of Iran donated a pavilion to the United Nations Office in Vienna, inaugurated at Vienna International Center. In 2016, three statues of Khayyam were unveiled: one at the University of Oklahoma, one in Nishapur and one in Florence, Italy. Over 150 composers have used the Rubaiyat as their source of inspiration. The earliest such composer was Liza Lehmann.
FitzGerald rendered Khayyam's name as "Tentmaker", and the anglicized name of "Omar the Tentmaker" resonated in English-speaking popular culture for a while. Thus, Nathan Haskell Dole published a novel called Omar, the Tentmaker: A Romance of Old Persia in 1898. Omar the Tentmaker of Naishapur is a historical novel by John Smith Clarke, published in 1910. "Omar the Tentmaker" is also the title of a 1914 play by Richard Walton Tully in an oriental setting, adapted as a silent film in 1922. US General Omar Bradley was given the nickname "Omar the Tent-Maker" in World War II.
The diverse talents and intellectual pursuits of Khayyam captivated many Ottoman and Turkish writers throughout history. Scholars often viewed Khayyam as a means to enhance their own poetic prowess and intellectual depth, drawing inspiration and recognition from his writings. For many Muslim reformers, Khayam's verses provided a counterpoint to the conservative norms prevalent in Islamic societies, allowing room for independent thought and a libertine lifestyle. Figures like Abdullah Cevdet, Rıza Tevfik, and Yahya Kemal utilized Khayyam's themes to justify their progressive ideologies or to celebrate liberal aspects of their lives, portraying him as a cultural, political, and intellectual role model who demonstrated Islam's compatibility with modern conventions. Similarly, Turkish leftist poets and intellectuals, including Nâzım Hikmet, Sabahattin Eyüboğlu, A. Kadir, and Gökçe, appropriated Khayyam to champion their socialist worldview, imbuing his voice with a humanistic tone in the vernacular. Khayyam's resurgence in spoken Turkish since the 1980s has transformed him into a poet of the people, with numerous books and translations revitalizing his historical significance. Conversely, scholars like Dāniş, Tevfik, and Gölpınarlı advocated for source criticism and the identification of authentic quatrains to discern the genuine Khayyam amidst historical perceptions of his sociocultural image.
The Moving Finger quatrain

The quatrain by Omar Khayyam known as "The Moving Finger", in the form of its translation by the English poet Edward Fitzgerald is one of the most popular quatrains in the Anglosphere. It reads:
The Moving Finger writes; and having writ,
Moves on: nor all your Piety nor Wit
Shall lure it back to cancel half a Line,
Nor all your Tears wash out a Word of it.
The title of the novel The Moving Finger written by Agatha Christie and published in 1942 was inspired by this quatrain of the translation of Rubaiyat of Omar Khayyam by Edward Fitzgerald. Martin Luther King also cites this quatrain of Omar Khayyam in one of his speeches, "Beyond Vietnam: A Time to Break Silence":
“We may cry out desperately for time to pause in her passage, but time is adamant to every plea and rushes on. Over the bleached bones and jumbled residues of numerous civilizations are written the pathetic words, ‘Too late.’ There is an invisible book of life that faithfully records our vigilance or our neglect. Omar Khayyam is right: ‘The moving finger writes, and having writ moves on.’”
In one of his apologetic speeches about the Clinton–Lewinsky scandal, Bill Clinton, the 42nd president of the US, also cites this quatrain.
Other popular culture references
In 1934 Harold Lamb published a historical novel Omar Khayyam. The French-Lebanese writer Amin Maalouf based the first half of his historical fiction novel Samarkand on Khayyam's life and the creation of his Rubaiyat. The sculptor Eduardo Chillida produced four massive iron pieces titled Mesa de Omar Khayyam (Omar Khayyam's Table) in the 1980s.
The lunar crater Omar Khayyam was named in his honour in 1970, as was the minor planet 3095 Omarkhayyam discovered by Soviet astronomer Lyudmila Zhuravlyova in 1980.
Google has released two Google Doodles commemorating him. The first was on his 964th birthday on 18 May 2012. The second was on his 971st birthday on 18 May 2019.
Gallery
-
 "A Ruby kindles in the vine", illustration for FitzGerald's Rubaiyat of Omar Khayyam by Adelaide Hanscom Leeson (c. 1905).
"A Ruby kindles in the vine", illustration for FitzGerald's Rubaiyat of Omar Khayyam by Adelaide Hanscom Leeson (c. 1905).
-
 "At the Tomb of Omar Khayyam" by Jay Hambidge (1911).
"At the Tomb of Omar Khayyam" by Jay Hambidge (1911).
-
 The statue of Khayyam in United Nations Office in Vienna as a part of Persian Scholars Pavilion donated by Iran.
The statue of Khayyam in United Nations Office in Vienna as a part of Persian Scholars Pavilion donated by Iran.
-
 Statue of Omar Khayyam in Bucharest
Statue of Omar Khayyam in Bucharest
-
 Monument to Omar Khayyam in Ciudad Universitaria of Madrid
Monument to Omar Khayyam in Ciudad Universitaria of Madrid
See also
Notable films
Noted Khayyamologists
Notes
- [oˈmæɾ xæjˈjɒːm]; /kaɪˈjɑːm, kaɪˈjæm/
- With an error of one day accumulating over 5,000 years, it was more precise than the Gregorian calendar of 1582, which has an error of one day every 3,330 years.
- E.g., in Rashid-al-Din Hamadani, or in Munis al-ahrar.
- In e.g., al-Qifti, or Bayhaqi.
- Katz (1998), p. 270. Excerpt: In some sense, his treatment was better than Ibn al-Haytham's because he explicitly formulated a new postulate to replace Euclid's rather than have the latter hidden in a new definition.
- O'Connor & Robertson (July 1999): However, Khayyam himself seems to have been the first to conceive a general theory of cubic equations.
- E.g., by the author of Firdaws al-tawārikh, author of Tārikh alfī, and al-Isfahani.
-
بر لوح نشان بودنیها بودهست
پیوسته قلم ز نیک و بد فرسودهست
در روز ازل هر آنچه بایست بداد
غم خوردن و کوشیدن ما بیهودهست
References
- ^ Tikkanen, Amy (28 February 2023). "Omar Khayyam: Persian poet and astronomer". Encyclopaedia Britannica. Retrieved 5 April 2023.
- ^ Nasr, S.H.; Aminrazavi, M.; with the assistance of M. R. Jozi (2008). An Anthology of Philosophy in Persia. Volume I: From Zoroaster to Omar Khayyam. London & New York: I.B. Tauris, in association with The Institute of Ismaili Studies London. ISBN 978-1-84511-541-8.
- Dehkhoda, A.A. "Khayyam". Lūght-nāmah (in Persian). Tehran.
- Levy, Reuben (2011) . The Persian Language. Routledge Library Editions: Iran, Volume: XV. London & New York: Routledge. ISBN 978-0-203-83301-8.
- ^ O'Connor, John J.; Robertson, Edmund F. (July 1999), "Omar Khayyam", MacTutor History of Mathematics Archive, University of St Andrews
- ^ Struik, D.J. (1958). "Omar Khayyam, mathematician". The Mathematics Teacher. LII (4): 280–285. JSTOR 27955652.
- ^ Boyle, J.A. (2007) . "'Umar Khayyām: Astronomer, Mathematician and Poet". In Richard N. Frye (ed.). The Cambridge History of Iran. Volume IV: From the Arab Invasion to the Saljuqs. New York: Cambridge University Press. pp. 658–664. doi:10.1017/CHOL9780521200936.023. ISBN 978-0-521-20093-6.
- ^ Aminrazavi, M. (2007). The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam. Oxford: Oneworld. ISBN 978-1-85168-355-0.
- Arberry, A.J. (2008). Aspects of Islamic Civilization: As Depicted in the Original Texts. Routledge. p. 16. ISBN 978-0-415-42600-8.
Omar composed his shafts of wit and shapes of beauty in his native Persian, which by the tenth century had recovered from the stunning blow dealt it by Arabic.
- Al-Khalili, Jim (30 September 2010). Pathfinders: The Golden Age of Arabic Science. Penguin UK. ISBN 978-0-14-196501-7.
Later, al-Karkhi (correct: al-Karaji), Ibn Tahir and the great Ibn al-Haytham in the tenth/eleventh century took it further by considering cubic and quartic equations, followed by the Persian mathematician and poet Omar Khayyam in the eleventh century.
- ^ Fouchécour, Charles-Henri de; Rosenfeld, Boris A. (1954–2007) . "ʿUmar K̲h̲ayyām". In H. A. R. Gibb; et al. (eds.). Encyclopaedia of Islam. Vol. X (2nd ed.). Leiden: Brill. pp. 827b – 834a. doi:10.1163/1573-3912_islam_COM_1284. ISBN 90-04-07026-5.
- Peter Avery and John Heath-Stubbs, The Ruba'iyat of Omar Khayyam, (Penguin Group, 1981), 14; "These dates, 1048–1031, tell us that Khayyam lived when the Seljuq Turkish Sultans were extending and consolidating their power over Persia and when the effects of this power were particularly felt in Nishapur, Khayyam's birthplace."
- Browne, E.G. (1899). "Yet More Light on 'Umar-i-Khayyām". Journal of the Royal Asiatic Society of Great Britain and Ireland. XXXI (2): 409–420. doi:10.1017/S0035869X00026538. JSTOR 25208104. S2CID 163490581.
- Ross, E.D. (1927). "'Omar Khayyam". Bulletin of the School of Oriental Studies. IV (3): 433–439. doi:10.1017/S0041977X00102897. JSTOR 606948. S2CID 246638673.
- ^ Boyle, J.A. (1966). "Omar Khayyām: Astronomer, Mathematician and Poet". Bulletin of the John Rylands Library. LII (1): 30–45. doi:10.7227/BJRL.52.1.3.
- ^ Ross, E.D.; Gibb, H.A.R. (1929). "The Earliest Account of 'Umar Khayyām". Bulletin of the School of Oriental Studies. V (3): 467–473. doi:10.1017/S0041977X00084615. JSTOR 607341. S2CID 177947195.
- ^ Meyerhof, Max (1948). "ʿAlī al-Bayhaqī's Tatimmat Siwān al-Hikma: A Biographical Work on Learned Men of the Islam". Osiris. VIII: 122–217. doi:10.1086/368514. JSTOR 301524.
- ^ Sarton, G. (1938). "The Tomb of Omar Khayyâm". Isis. XXIX (1): 15–19. doi:10.1086/347379. JSTOR 225920. S2CID 143678233.
- ^ Edward FitzGerald, Rubaiyat of Omar Khayyam, Ed. Christopher Decker, (University of Virginia Press, 1997), xv; "The Seljuq Turks had invaded the province of Khorasan in the 1030s, and the city of Nishapur surrendered to them voluntarily in 1038. Thus Omar Khayyam grew to maturity during the first of the several alien dynasties that would rule Iran until the twentieth century".
- Rosenfeld, Boris A. (2016). "Umar al-Khayyām". In Helaine Selin (ed.). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (3rd ed.). Dordrecht: Springer–Verlag. pp. 4330b – 4332a. doi:10.1007/978-94-007-7747-7_9775. ISBN 978-94-007-7747-7.
- Aminrazavi, M. (2010). "Review: Omar Khayyam: Poet, Rebel, Astronomer, Hazhir Teimourian". Iranian Studies. XLIII (4): 569–571. doi:10.1080/00210862.2010.495592. JSTOR 23033230. S2CID 162241136.
- ^ Mohamed, Mohaini (2000). Great Muslim Mathematicians. Malaysia: Penerbit Universiti Teknologi Malaysia. ISBN 983-52-0157-9.
- Lamb, Evelyn (28 October 2014). "In Which Omar Khayyam Is Grumpy with Euclid". Scientific American Blog Network. Retrieved 10 September 2023.
- ^ Vahabzadeh, Bijan (7 May 2014). Ehsan Yarshater (ed.). "Khayyam, Omar xv. As Mathematician". Encyclopædia Iranica. Encyclopædia Iranica Foundation. Retrieved 8 September 2023.
- ^ Yuschkevich, Adolph P.; Rosenfeld, Boris A. (1970–1980) . "Khayyāmī (or Khayyām)". In Charles Coulston Gillispie (ed.). Dictionary of Scientific Biography. Vol. VII. New York: Charles Scribner’s Sons. pp. 323b – 334a. ISBN 0-684-16962-2.
- Nethington, Amanda (2020). "Achieving Philosophical Perfection: Omar Khayyam's Successful Replacement of Euclid's Parallel Postulate" (PDF). Lucerna: Honors Undergraduate Journal. XIV: 72–97. hdl:10355/74778.
- Rosenfeld, Boris A. (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Studies in the History of Mathematics and Physical Sciences. Vol. 12. Translated by Abe Shenitzer, with the editorial assistance of Hardy Grant. New York: Springer. doi:10.1007/978-1-4419-8680-1. ISBN 978-1-4419-8680-1. ISSN 0172-570X.
- ^ Katz, V. (1998). A History of Mathematics: An Introduction (2nd ed.). Addison-Wesley. ISBN 0-321-01618-1.
- Rosenfeld, Boris A.; Youschkevitch, A.P. (1996). "Geometry". In Roshdi Rashed; in collaboration with Régis Morelon (eds.). Encyclopedia of the History of Arabic Science. Vol. II. London & New York: Routledge. pp. 115–159. ISBN 0-415-02063-8.
- Rolwing, Raymond H.; Levine, Maita (1969). "The Parallel Postulate". The Mathematics Teacher. LXII (8): 665–669. JSTOR 27958258.
- Smith, D.E. (1935). "Euclid, Omar Khayyâm, and Saccheri". Scripta Mathematica. III (1): 5–10. OCLC 14156259.
- Vahabzadeh, Bijan (2005). Jafar Aghayani-Chawoshi (ed.). "Omar Khayyam and the Concept of Irrational Numbers". Farhang: Quarterly Journal of Humanities and Cultural Studies. Issue Topic: Commemoration of Khayyam (3). XVIII (53–54): 125–134.
- ^ Cooper, Glen M. (2003). "Review: Omar Khayyam, the Mathmetician by R. Rashed, B. Vahabzadeh". Journal of the American Oriental Society. CXXIII (1): 248–249. doi:10.2307/3217882. JSTOR 3217882.
- Eves, H. (1958). "Omar Khayyam's Solution of Cubic Equations". Mathematics Teacher. LI (4): 285–286. doi:10.5951/MT.51.4.0285. JSTOR 27955653.
- "Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics." → Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter, V (4): 8–12, doi:10.2307/3027812, JSTOR 3027812, S2CID 125245433
- Netz, Reviel (1999). "Archimedes Transformed: The Case of a Result Stating a Maximum for a Cubic Equation". Archive for History of Exact Sciences. LIV (1): 1–47. doi:10.1007/s004070050032. JSTOR 41134072. S2CID 121468528.
- Oaks, Jeffrey A. (2011). "Khayyām's Scientific Revision of Algebra" (PDF). Suhayl: International Journal for the History of the Exact and Natural Sciences in Islamic Civilisation. X: 47–75.
- ^ Kent, Deborah A.; Muraki, David J. (2016). "A Geometric Solution of a Cubic by Omar Khayyam … in Which Colored Diagrams Are Used Instead of Letters for the Greater Ease of Learners". The American Mathematical Monthly. CXXIII (2): 149–160. doi:10.4169/amer.math.monthly.123.2.149. JSTOR 123.2.149. S2CID 124153443.
- ^ Kennedy, Evelyn (1966). "'Omar Khayyam". The Mathematics Teacher. LIX (3): 140–142. doi:10.5951/MT.59.2.0140. JSTOR 27957296.
- Amir-Moez, A.R. (1963). "A Paper of Omar Khayyam". Scripta Mathematica. XXVI: 323–337.
- "Review: The Algebra of Omar Khayyam by Daoud Kasir". The Mathematics Teacher. XXV (4): 238–241. 1932. JSTOR 27951448.
- Amir-Moez, A. R. (1962). "Khayyam's Solution of Cubic Equations". Mathematics Magazine. XXXV (5): 269–271. doi:10.2307/2688197. JSTOR 2688197.
This paper contains an extension by Mohsen Hashtroodi of Khayyam's method to degree four equations.
- Waerden, B.L. (2013). A History of Algebra: From al-Khwārizmī to Emmy Noether. New York: Springer Science & Business Media. ISBN 978-3-642-51599-6.
- Van Brummelen, Glen (2014). "A Survey of Research in the Mathematical Sciences in Medieval Islam from 1996 to 2011". In Nathan Sidoli; Glen Van Brummelen (eds.). From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren. New York: Springer. pp. 101–138. doi:10.1007/978-3-642-36736-6_6. ISBN 978-3-642-36736-6.
- Knoebel, Art; Laubenbacher, Reinhard; Lodder, Jerry (2007). Mathematical Masterpieces: Further Chronicles by the Explorers. Springer. ISBN 978-0-387-33060-0.
- ^ Whinfield, E.H. (2000). The Quatrains of Omar Khayyam: The Persian Text with an English Verse Translation. New York: Psychology Press Ltd.
- O'Connor, John J.; Robertson, E.F. (2006). "Muslim Extraction of Roots". MacTutor History of Mathematics Archive. University of St Andrews.
- Coolidge, J.L. (1985). "The Story of the Binomial Theorem". American Mathematical Monthly. LVI (3): 147–157. doi:10.2307/2305028. JSTOR 2305028.
- Nichols, Susan (2017). Al-Karaji: Tenth-Century Mathematician and Engineer. New York: Rosen Publishing.
- Akrami, Musa (11 February 2014). "The Development of Iranian Calendar: Historical and Astronomical Foundations". arXiv:1111.4926v2 .
- Abdollahy, Reza (15 December 1990). Ehsan Yarshater (ed.). "Calendars ii. In the Islamic period". Encyclopaedia Iranica. Encyclopaedia Iranica Foundation. Retrieved 21 November 2017.
- Farrell, Charlotte (1996). "The Ninth-century Renaissance in Astronomy". The Physics Teacher. XXXIV (5): 268–272. Bibcode:1996PhTea..34..268F. doi:10.1119/1.2344432.
- Heydari-Malayeri, M. (21 October 2004). "Concise Review of the Iranian Calendar". arXiv:astro-ph/0409620v2.
- Saliba, G. (2002). "Review: Al-Khayyām Mathématicien, by R. Rashed; B. Vahabzadeh; Omar Khayyam the Mathematician, by R. Rashed; B. Vahabzadeh". Iranian Studies. XXXV (1–3): 220–225. doi:10.1017/S0021086200003686. JSTOR 4311451.
- ^ Ali Dashti (translated by L. P. Elwell-Sutton), In Search of Omar Khayyam, Routledge Library Editions: Iran (2012)
- ^ Ross, E.D. (1927). "'Omar Khayyam". Bulletin of the School of Oriental Studies. IV (3): 433–439. doi:10.1017/S0041977X00102897. JSTOR 606948. S2CID 246638673.
- ^ Blois, François de (2004). Persian Literature - A Bio-Bibliographical Survey. Volume 5: Poetry of the Pre-Mongol Period. London & New York: Routledge. ISBN 9780947593476.
- Ambrose George Potter, A Bibliography of the Rubaiyat of Omar Khayyam (1929).
- Moss, Joyce (2004). Middle Eastern Literature and Their times. Thomson Gale. ISBN 9780787637316.
- Boscaglia, Fabrizio (2015). "Pessoa, Borges and Khayyam". Variaciones Borges. XL (40): 41–64. JSTOR 24881234.
- ^ Ross, E.D. (1898). "Musaffariyé: Containing a Recent Contribution to the Study of 'Omar Khayyām". Journal of the Royal Asiatic Society of Great Britain and Ireland. XXX (2): 349–366. doi:10.1017/S0035869X00025235. JSTOR 25207968. S2CID 162611227.
- Aminrazavi, M.; Van Brummelen, G. (Spring 2017). "Umar Khayyam". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ^ Bowen, J.C.E. (1973). "The Rubāՙiyyāt of Omar Khayyam: A Critical Assessment of Robert Graves' and Omar Ali Shah's Translation". Iran. XI: 63–73. doi:10.2307/4300485. JSTOR 4300485.
- Davis, D. (31 January 2012). Ehsan Yarshater (ed.). "Fitzgerald, Edward". Encyclopaedia Iranica. Encyclopaedia Iranica Foundation. Retrieved 15 January 2017.
- FitzGerald, E. (2010). Rubaiyat of Omar Khayyam (p. 12). Champaign, Ill.: Project Gutenberg
- Schenker, D. (1981). "Fugitive Articulation: An Introduction to The Rubáiyát of Omar Khayyam". Victorian Poetry. XIX (1): 49–64.
- Hedayat's "Blind Owl" as a Western Novel. Princeton Legacy Library: Michael Beard
- Katouzian, H. (1991). Sadeq Hedayat: The life and literature of an Iranian writer. London: I.B. Tauris
- Hitchens, C. (2007). The portable atheist: Essential readings for the nonbeliever. Philadelphia, PA: Da Capo.
- ^ Khayyam, Omar (18 May 2017). The World in Pictures. Omar Khayyam. Rubáyát. Aegitas Publishing. ISBN 9781773132372.
- Robertson, J.M. (2016). A Short History of Freethough: Ancient and Modern.
- Hidāyat, S.; Khayyam, Omar (1993). Les chants d'Omar Khayam. Paris: José Corti. ISBN 9782714304896.
- Gsillik, B. (1960). "The Real 'Omar Khayyām". Acta Orientalia Academiae Scientiarum Hungaricae. X (1): 59–77. JSTOR 23682646.
- Albano, Giuseppe (2008). "The Benefits of Reading the "Rubáiyát of Omar Khayyám" as Pastoral". Victorian Poetry. XLVI (1): 55–67. doi:10.1353/vp.0.0010. JSTOR 40347527. S2CID 170388817.
- Bjerregaard, C.H.A. (1915). Omar Khayyam, FitzGerald, Edward, 1809-1883, Sufism. London: Sufi Publishing Society.
- Idries Shah, The Sufis, Octagon Press (1999)
- "Every line of the Rubaiyat has more meaning than almost anything you could read in Sufi literature" Abdullah Dougan Who is the Potter? Gnostic Press 1991 ISBN 0-473-01064-X
- Nasr, S. H. (2006). Islamic Philosophy from its Origin to the Present: Philosophy in the Land of Prophecy. New York: SUNY Press. ISBN 0-7914-6799-6.
- Beveridge, H. (1905). "Omar Khayyam". Journal of the Royal Asiatic Society. XXXVII (3): 521–526. doi:10.1017/S0035869X00033530. JSTOR 25210170.
- J. D. Yohannan, Persian Poetry in England and America, 1977.
- Seyed-Gohrab, A.A., ed. (2012). The Great 'Umar Khayyam: A Global Reception of the Rubáiyát (PDF). Leiden: Leiden University Press. ISBN 978-94-0060-079-9.
- Simidchieva, M. (2011). FitzGerald's Rubáiyát and Agnosticism. In A. Poole, C. Van Ruymbeke, & W. Martin (Eds.), FitzGerald's Rubáiyát of Omar Khayyám: Popularity and Neglect. Anthem Press.
- UNIS. "Monument to Be Inaugurated at the Vienna International Centre, 'Scholars Pavilion' donated to International Organizations in Vienna by Iran".
- "Khayyam statue finally set up at University of Oklahoma". Tehran Times. Archived from the original on 5 April 2016. Retrieved 4 April 2016.
- Martin, William H.; Mason, Sandra (15 July 2009). Ehsan Yarshater (ed.). "Khayyam, Omar xiii. Musical Works Based On The Rubaiyat". Encyclopædia Iranica. Encyclopædia Iranica Foundation. Retrieved 8 October 2023.
- Jeffrey D. Lavoie, The Private Life of General Omar N. Bradley (2015)
- Balıkçıoğlu, Efe Murat (2024). "Quatrains of Many Receptions: A Survey of Perceptions of 'Omar Khayyām in Ottoman and Turkish Translations". Iranian Studies: 1. doi:10.1017/irn.2023.72.
- ^ Balıkçıoğlu, Efe Murat (2024). "Quatrains of Many Receptions: A Survey of Perceptions of 'Omar Khayyā m in Ottoman and Turkish Translations". Iranian Studies: 1, 22. doi:10.1017/irn.2023.72.
- ^ Seyed-Gohrab, A.A. (13 April 2018). "The Moving Finger: Glimpses into the Life of a Persian Quatrain". Leiden Medievalists Blog. Universiteit Leiden. Retrieved 14 May 2022.
- FitzGerald, Stanza LXXI, 4th ed.
- "17. MLK Beyond Vietnam.pdf (hawaii.edu)" (PDF). Archived (PDF) from the original on 10 October 2022.
- "Quatrain 36". exploring khayyaam -US. 21 December 2006. Retrieved 14 May 2022.
- Omar Khayyam's Table II Retrieved 8 August 2021.
- Omar Khayyam's Table III Retrieved 8 August 2021.
- Dictionary of Minor Planet Names. 1979. p. 255. Retrieved 8 September 2012 – via Google Books.
- "How Omar Khayyam changed the way people measure time". The Independent. 17 May 2019. Archived from the original on 24 May 2022. Retrieved 18 May 2019.
Further reading
- Biegstraaten, Jos (2008). "Omar Khayyam (Impact On Literature And Society In The West)". Encyclopaedia Iranica. Vol. 15. Encyclopaedia Iranica Foundation.
- Boyle, J. A., ed. (1968). The Cambridge History of Iran. Volume V: The Saljug and Mongol Periods. New York: Cambridge University Press. ISBN 978-0-521-06936-6.
- Rypka, J. (1968). Karl Jahn (ed.). History of Iranian Literature. Dordrecht: D. Reidel. ISBN 978-94-010-3481-4.
- Turner, Howard R. (1997). Science in Medieval Islam: An Illustrated Introduction. University of Texas Press. ISBN 0-292-78149-0.
External links
- Works by or about Omar Khayyam at the Internet Archive
- Works by Omar Khayyam at LibriVox (public domain audiobooks)

- Hashemipour, Behnaz (2007). "Khayyām: Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyāmī al-Nīshāpūrī". In Thomas Hockey; et al. (eds.). The Biographical Encyclopedia of Astronomers. New York: Springer. pp. 627–8. ISBN 978-0-387-31022-0. (PDF version.)
- Umar Khayyam, in the Stanford Encyclopedia of Philosophy
- The illustrated Rubáiyát of Omar Khayyám at the Internet Archive
| Mathematics in Iran | |||||||
|---|---|---|---|---|---|---|---|
| Mathematicians |
|  | |||||
| Prize Recipients |
| ||||||
| Organizations | |||||||
| Institutions | |||||||
| People of Khorasan | |
|---|---|
| Scientists | |
| Philosophers | |
| Islamic scholars |
|
| Poets and artists | |
| Historians and political figures |
|
- Omar Khayyam
- 1048 births
- 1131 deaths
- 11th-century Iranian astronomers
- 11th-century Persian-language poets
- 11th-century Persian-language writers
- 12th-century astronomers
- 12th-century Iranian astronomers
- 12th-century Iranian mathematicians
- 12th-century Persian-language poets
- 12th-century Persian-language writers
- Algebraists
- Astronomers of the medieval Islamic world
- Iranian philosophers
- Mathematicians from Nishapur
- Medieval Iranian physicists
- Persian-language spiritual writers
- Philosophers from Nishapur
- Poets from the Seljuk Empire
- Scholars from the Seljuk Empire
 th root of natural numbers using a law he had discovered which did not depend on geometric figures. This book was most likely titled the Difficulties of Arithmetic (Mushkilāt al-Ḥisāb), and is not extant. Based on the context, some historians of mathematics such as D. J. Struik, believe that Omar must have known the formula for the expansion of the binomial
th root of natural numbers using a law he had discovered which did not depend on geometric figures. This book was most likely titled the Difficulties of Arithmetic (Mushkilāt al-Ḥisāb), and is not extant. Based on the context, some historians of mathematics such as D. J. Struik, believe that Omar must have known the formula for the expansion of the binomial  , where n is a positive integer. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyam was the
, where n is a positive integer. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyam was the