| Revision as of 21:21, 28 January 2008 edit99.248.22.88 (talk) →Third law← Previous edit | Latest revision as of 21:11, 23 December 2024 edit undoFavonian (talk | contribs)Autopatrolled, Administrators287,697 editsm Reverted edit by 2605:8D80:501:70EE:3ABA:DADE:D93E:C1D2 (talk) to last version by PlasticwonderTag: Rollback | ||
| Line 1: | Line 1: | ||
| {{short description|Observational basis of thermodynamics}} | |||
| {{Thermodynamic equations| laws=true}} | |||
| {{Thermodynamics|cTopic=Laws}} | |||
| The '''laws of thermodynamics''', in principle, describe the specifics for the transport of ] and ] in ]. Since their conception, however, these ]s have become some of the most important in all of ] and other branches of ] connected to ]. They are often associated with concepts far beyond what is directly stated in the wording. | |||
| The '''laws of thermodynamics''' are a set of ]s which define a group of ], such as ], ], and ], that characterize ]s in ]. The laws also use various parameters for ]es, such as ] and ], and establish relationships between them. They state ] that form a basis of precluding the possibility of certain phenomena, such as ]. In addition to their use in ], they are important fundamental ] of ] in general and are applicable in other natural ]. | |||
| == History== | |||
| The first established principle of thermodynamics (which eventually became the Second Law) was formulated by ] in 1824. By 1860, as found in the works of those as ] and ], there were two established "principles" of thermodynamics, the first principle and the second principle. As the years passed, these principles turned into "laws." By 1873, for example, thermodynamicist ], in his “Graphical Methods in the Thermodynamics of Fluids”, clearly stated that there were two absolute laws of thermodynamics, a first law and a second law. | |||
| Traditionally, thermodynamics has recognized three fundamental laws, simply named by an ordinal identification, the first law, the second law, and the third law.<ref name="Guggenheim 1985">Guggenheim, E.A. (1985). ''Thermodynamics. An Advanced Treatment for Chemists and Physicists'', seventh edition, North Holland, Amsterdam, {{ISBN|0-444-86951-4}}.</ref><ref name="Kittel and Kroemer 1980">Kittel, C. Kroemer, H. (1980). ''Thermal Physics'', second edition, W.H. Freeman, San Francisco, {{ISBN|0-7167-1088-9}}.</ref><ref name="Adkins 1968">Adkins, C.J. (1968). ''Equilibrium Thermodynamics'', McGraw-Hill, ], {{ISBN|0-07-084057-1}}.</ref> A more fundamental statement was later labelled as the zeroth law after the first three laws had been established. | |||
| Presently, there are a total of five laws. Over the last 80 years or so, occasionally, various writers have suggested adding Laws, but none of them have been widely accepted. | |||
| The ] defines ] and forms a basis for the definition of temperature: if two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other. | |||
| ==Overview== | |||
| The ] states that, when energy passes into or out of a system (as ], ], or ]), the system's ] changes in accordance with the law of ]. | |||
| :* ] | |||
| :*:<math>A \sim B \wedge B \sim C \Rightarrow A \sim C</math> | |||
| The ] states that in a natural ], the sum of the ] of the interacting ]s never decreases. A common corollary of the statement is that heat does not spontaneously pass from a colder body to a warmer body. | |||
| :* ] | |||
| :*:<math>\mathrm{d}U=\delta Q-\delta W\,</math> | |||
| The ] states that a system's entropy approaches a constant value as the temperature approaches ]. With the exception of non-crystalline solids (]es), the entropy of a system at absolute zero is typically close to zero.<ref name="Kittel and Kroemer 1980"/> | |||
| :* ] | |||
| :*:<math>\oint \frac{\delta Q}{T} \ge 0</math> | |||
| The first and second laws prohibit two kinds of perpetual motion machines, respectively: the ] which produces work with no energy input, and the ] which spontaneously converts thermal energy into mechanical work. | |||
| :* ] | |||
| :*: <math> T \rightarrow 0, S \rightarrow C </math> | |||
| == History == | |||
| :* ] - sometimes called the ''Fourth Law of Thermodynamics'' | |||
| {{main|History of thermodynamics}} | |||
| :*: <math> \mathbf{J}_{u} = L_{uu}\, \nabla(1/T) - L_{ur}\, \nabla(m/T) \!</math>; | |||
| {{see also|Timeline of thermodynamics}} | |||
| :*: <math> \mathbf{J}_{r} = L_{ru}\, \nabla(1/T) - L_{rr}\, \nabla(m/T) \!</math>. | |||
| The history of thermodynamics is fundamentally interwoven with the ] and the ], and ultimately dates back to theories of heat in antiquity. The laws of thermodynamics are the result of progress made in this field over the nineteenth and early twentieth centuries. The first established thermodynamic principle, which eventually became the second law of thermodynamics, was formulated by ] in 1824 in his book '']''. By 1860, as formalized in the works of scientists such as ] and ], what are now known as the first and second laws were established. Later, ] (or Nernst's postulate), which is now known as the third law, was formulated by ] over the period 1906–1912. While the numbering of the laws is universal today, various textbooks throughout the 20th century have numbered the laws differently. In some fields, the second law was considered to deal with the efficiency of heat engines only, whereas what was called the third law dealt with entropy increases. Gradually, this resolved itself and a zeroth law was later added to allow for a self-consistent definition of temperature. Additional laws have been suggested, but have not achieved the generality of the four accepted laws, and are generally not discussed in standard textbooks. | |||
| == Zeroth law == | == Zeroth law == | ||
| The ] provides for the foundation of temperature as an empirical parameter in thermodynamic systems and establishes the ] between the temperatures of multiple bodies in thermal equilibrium. The law may be stated in the following form: | |||
| {{main|Zeroth law of thermodynamics}} | |||
| {{quote|If two systems are both in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.<ref>Guggenheim (1985), p. 8.</ref>}} | |||
| Though this version of the law is one of the most commonly stated versions, it is only one of a diversity of statements that are labeled as "the zeroth law". Some statements go further, so as to supply the important physical fact that temperature is one-dimensional and that one can conceptually arrange bodies in a real number sequence from colder to hotter.<ref>Sommerfeld, A. (1951/1955). ''Thermodynamics and Statistical Mechanics'', vol. 5 of ''Lectures on Theoretical Physics'', edited by F. Bopp, J. Meixner, translated by J. Kestin, Academic Press, New York, p. 1.</ref><ref>] (1978). The concepts of thermodynamics, in ''Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977'', edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, {{ISBN|0-444-85166-6}}, pp. 411–51.</ref><ref>] (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pp. 3–32, in ''New Perspectives in Thermodynamics'', edited by J. Serrin, Springer, Berlin, {{ISBN|3-540-15931-2}}.</ref> | |||
| {{cquote|If two thermodynamic systems are each in thermal equilibrium with a third, then they are in thermal equilibrium with each other.}} | |||
| These concepts of temperature and of thermal equilibrium are fundamental to thermodynamics and were clearly stated in the nineteenth century. The name 'zeroth law' was invented by ] in the 1930s, long after the first, second, and third laws were widely recognized. The law allows the definition of temperature in a non-circular way without reference to entropy, its ]. Such a temperature definition is said to be 'empirical'.<ref>Adkins, C.J. (1968/1983). ''Equilibrium Thermodynamics'', (first edition 1968), third edition 1983, Cambridge University Press, {{ISBN|0-521-25445-0}}, pp. 18–20.</ref><ref>Bailyn, M. (1994). ''A Survey of Thermodynamics'', American Institute of Physics Press, New York, {{ISBN|0-88318-797-3}}, p. 26.</ref><ref>Buchdahl, H.A. (1966), ''The Concepts of Classical Thermodynamics'', Cambridge University Press, London, pp. 30, 34ff, 46f, 83.</ref><ref>*Münster, A. (1970), ''Classical Thermodynamics'', translated by E.S. Halberstadt, Wiley–Interscience, London, {{ISBN|0-471-62430-6}}, p. 22.</ref><ref>] (1957/1966). ''Elements of Classical Thermodynamics for Advanced Students of Physics'', original publication 1957, reprint 1966, Cambridge University Press, Cambridge, p. 10.</ref><ref>] (1966). ''Thermodynamics and Statistical Mechanics'', Cambridge University Press, London, pp. 4, 8, 68, 86, 97, 311.</ref> | |||
| When two systems are put in contact with each other, there will be a net exchange of ] between them unless or until they are in ], that is they contain the same amount of thermal energy for a given volume (say, 1 cubic centimetre, or 1 cubic inch.) While this is a fundamental concept of thermodynamics, the need to state it explicitly as a law was not perceived until the first third of the ], long after the first three laws were already widely in use, hence the zero numbering. The Zeroth Law asserts that thermal equilibrium, viewed as a ], is an ]. | |||
| == First law == | == First law == | ||
| {{see also|Thermodynamic cycle}} | |||
| {{main|First law of thermodynamics}} | |||
| The ] is a version of the law of ], adapted for thermodynamic processes. In general, the conservation law states that the total ] of an ] is constant; energy can be transformed from one form to another, but can be neither created nor destroyed. | |||
| {{quote|In a ] (i.e. there is no transfer of matter into or out of the system), the first law states that the change in ] of the system ({{math|Δ''U''<sub>system</sub>}}) is equal to the difference between the heat supplied to the system ({{math|''Q''}}) and the work ({{math|''W''}}) done ''by'' the system on its surroundings. (Note, an ], not used in this article, is to define {{math|''W''}} as the work done ''on'' the system by its surroundings): <math display="block">\Delta U_{\rm system} = Q - W.</math>}} | |||
| {{cquote|In any process, the total energy of the universe remains at large.}} | |||
| It can also be defined as: | |||
| {{cquote|for a thermodynamic cycle the sum of net heat | |||
| supplied to the system and the net work done by the system is equal to | |||
| zero.}} | |||
| For processes that include the transfer of matter, a further statement is needed. | |||
| More simply, the First Law states that energy cannot be created or destroyed; rather, the amount of energy lost in a steady state process cannot be greater than the amount of energy gained. | |||
| {{quote|When two initially isolated systems are combined into a new system, then the total internal energy of the new system, {{math|''U''<sub>system</sub>}}, will be equal to the sum of the internal energies of the two initial systems, {{math|''U''<sub>1</sub>}} and {{math|''U''<sub>2</sub>}}: <math display="block">U_{\rm system} = U_1 + U_2.</math>}} | |||
| This is the statement of ] for a ]. It refers to the two ways that a ] transfers energy to and from its surroundings - by the process of heating (or cooling) and the process of mechanical work. The rate of gain or loss in the stored energy of a system is determined by the rates of these two processes. In open systems, the flow of matter is another energy transfer mechanism, and extra terms must be included in the expression of the first law. | |||
| The First Law encompasses several principles: | |||
| The First Law clarifies the nature of energy. It is a stored quantity which is independent of any particular process path, i.e., it is independent of the system history. If a system undergoes a ], whether it becomes warmer, cooler, larger, or smaller, then it will have the same amount of energy each time it returns to a particular state. Mathematically speaking, energy is a ] and infinitesimal changes in the energy are ]s. | |||
| * ], which says that energy can be neither created nor destroyed, but can only change form. A particular consequence of this is that the total energy of an isolated system does not change. | |||
| * The concept of ] and its relationship to temperature. If a system has a definite temperature, then its total energy has three distinguishable components, termed ] (energy due to the motion of the system as a whole), ] (energy resulting from an externally imposed force field), and ]. The establishment of the concept of internal energy distinguishes the first law of thermodynamics from the more general law of conservation of energy. <math display="block">E_{\rm total} = KE_{\rm system} + PE_{\rm system} + U_{\rm system}</math> | |||
| * ] is a process of transferring energy to or from a system in ways that can be described by macroscopic mechanical forces acting between the system and its surroundings. The work done by the system can come from its overall kinetic energy, from its overall potential energy, or from its internal energy.{{pb}} For example, when a machine (not a part of the system) lifts a system upwards, some energy is transferred from the machine to the system. The system's energy increases as work is done on the system and in this particular case, the energy increase of the system is manifested as an increase in the system's ]. Work added to the system increases the potential energy of the system. | |||
| * When matter is transferred into a system, the internal energy and potential energy associated with it are transferred into the new combined system. <math display="block">\left( u \,\Delta M \right)_{\rm in} = \Delta U_{\rm system}</math> where {{math|''u''}} denotes the internal energy per unit mass of the transferred matter, as measured while in the surroundings; and {{math|Δ''M''}} denotes the amount of transferred mass. | |||
| * The flow of ] is a form of energy transfer. Heat transfer is the natural process of moving energy to or from a system, other than by work or the transfer of matter. In a ] system, the internal energy can only be changed by the transfer of energy as heat: <math display="block">\Delta U_{\rm system}=Q.</math> | |||
| Combining these principles leads to one traditional statement of the first law of thermodynamics: it is not possible to construct a machine which will perpetually output work without an equal amount of energy input to that machine. Or more briefly, a perpetual motion machine of the first kind is impossible. | |||
| All laws of thermodynamics but the First are statistical and simply describe the tendencies of macroscopic systems. For microscopic systems with few particles, the variations in the parameters become larger than the parameters themselves, and the assumptions of thermodynamics become meaningless. The First Law, i.e. the law of conservation, has become the most secure of all basic laws of science. At present, it is unquestioned. | |||
| == Second law == | == Second law == | ||
| The ] indicates the irreversibility of natural processes, and in many cases, the tendency of natural processes to lead towards spatial homogeneity of matter and energy, especially of temperature. It can be formulated in a variety of interesting and important ways. One of the simplest is the Clausius statement, that heat does not spontaneously pass from a colder to a hotter body. | |||
| {{main|Second law of thermodynamics}} | |||
| It implies the existence of a quantity called the ] of a thermodynamic system. In terms of this quantity it implies that | |||
| {{cquote|The ] of an ] not in ] will tend to increase over time, approaching a maximum value at equilibrium.}} | |||
| {{quote|When two initially isolated systems in separate but nearby regions of space, each in ] with itself but not necessarily with each other, are then allowed to interact, they will eventually reach a mutual thermodynamic equilibrium. The sum of the ] of the initially isolated systems is less than or equal to the total entropy of the final combination. Equality occurs just when the two original systems have all their respective intensive variables (temperature, pressure) equal; then the final system also has the same values.}} | |||
| The second law is applicable to a wide variety of processes, both reversible and irreversible. According to the second law, in a reversible heat transfer, an element of heat transferred, <math>\delta Q</math>, is the product of the temperature (<math>T</math>), both of the system and of the sources or destination of the heat, with the increment (<math>dS</math>) of the system's conjugate variable, its ] (<math>S</math>):<ref name="Guggenheim 1985"/> | |||
| In a simple manner, the second law states that "energy systems have a tendency to increase their entropy" rather than decrease it. | |||
| : <math>\delta Q = T\,dS\, .</math> | |||
| While reversible processes are a useful and convenient theoretical limiting case, all natural processes are irreversible. A prime example of this irreversibility is the transfer of heat by conduction or radiation. It was known long before the discovery of the notion of entropy that when two bodies, initially of different temperatures, come into direct thermal connection, then heat immediately and spontaneously flows from the hotter body to the colder one. | |||
| A way of looking at the second law for non-scientists is to look at entropy as a measure of ]. So, for example, a broken cup has less order and more chaos than an intact one. Likewise, solid ], the most organized form of matter, have very low entropy values; and ]es, which are highly disorganized, have high entropy values. | |||
| ] may also be viewed as a physical measure concerning the microscopic details of the motion and configuration of a system, when only the macroscopic states are known. Such details are often referred to as ''disorder'' on a microscopic or molecular scale, and less often as ]. For two given macroscopically specified states of a system, there is a mathematically defined quantity called the 'difference of information entropy between them'. This defines how much additional microscopic physical information is needed to specify one of the macroscopically specified states, given the macroscopic specification of the other – often a conveniently chosen reference state which may be presupposed to exist rather than explicitly stated. A final condition of a natural process always contains microscopically specifiable effects which are not fully and exactly predictable from the macroscopic specification of the initial condition of the process. This is why entropy increases in natural processes – the increase tells how much extra microscopic information is needed to distinguish the initial macroscopically specified state from the final macroscopically specified state.<ref>Ben-Naim, A. (2008). ''A Farewell to Entropy: Statistical Thermodynamics Based on Information'', World Scientific, New Jersey, {{ISBN|978-981-270-706-2}}.</ref> Equivalently, in a thermodynamic process, energy spreads. | |||
| The ] of a thermally isolated macroscopic system never decreases (see ]). However, a microscopic system may exhibit fluctuations of entropy opposite to that dictated by the Second Law (see ]). In fact, the mathematical proof of the Fluctuation Theorem from time-reversible dynamics and the ] constitutes a proof of the Second Law. In a logical sense the Second Law thus ceases to be a "Law" of physics and instead becomes a theorem which is valid for large systems or long times. | |||
| == Third law == | == Third law == | ||
| The ] can be stated as:<ref name="Kittel and Kroemer 1980"/> | |||
| {{quote|A system's entropy approaches a constant value as its temperature approaches ].}} | |||
| ] | |||
| {{cquote|As temperature approaches ], the ] of a system approaches a constant.}} | |||
| At absolute zero temperature, the system is in the state with the minimum thermal energy, the ]. The constant value (not necessarily zero) of entropy at this point is called the ] of the system. With the exception of non-crystalline solids (e.g. ]) the residual entropy of a system is typically close to zero.<ref name="Kittel and Kroemer 1980"/> However, it reaches zero only when the system has a unique ground state (i.e., the state with the minimum thermal energy has only one configuration, or ]). Microstates are used here to describe the probability of a system being in a specific state, as each microstate is ] to have the same probability of occurring, so ] with fewer microstates are less probable. In general, entropy is related to the number of possible microstates according to the ] | |||
| In brief, this postulates that entropy is temperature dependent and leads to the formulation of the idea of ]. | |||
| : <math>S = k_{\mathrm B}\, \mathrm{ln}\, \Omega</math> | |||
| a small penis is formed | |||
| where ''S'' is the entropy of the system, ''k''<sub>B</sub> is the ], and ''Ω'' the number of microstates. At absolute zero there is only 1 microstate possible (''Ω'' = 1 as all the atoms are identical for a pure substance, and as a result all orders are identical as there is only one combination) and <math>\ln(1)=0</math>. | |||
| == |
== Onsager relations == | ||
| The ] have been considered the fourth law of thermodynamics.<ref>{{cite journal|last=Wendt|first=Richard P.|year=1974|title=Simplified transport theory for electrolyte solutions|journal=Journal of Chemical Education|publisher=American Chemical Society (ACS)|volume=51|issue=10|page=646|doi=10.1021/ed051p646|bibcode=1974JChEd..51..646W |issn=0021-9584}}</ref><ref name=":0">{{Cite book|last=Deffner|first=Sebastian|url=https://www.worldcat.org/oclc/1112388794|title=Quantum thermodynamics : an introduction to the thermodynamics of quantum information|date=2019|others=Steve Campbell, Institute of Physics|isbn=978-1-64327-658-8 |location=San Rafael, CA |oclc=1112388794 |publisher=Morgan & Claypool Publishers}}</ref><ref>{{cite encyclopedia |title=Lars Onsager – American chemist |type=biography |encyclopedia=] |lang=en |url=https://www.britannica.com/biography/Lars-Onsager |access-date=2021-03-10}}</ref> They describe the relation between thermodynamic flows and forces in ], under the assumption that thermodynamic variables can be defined locally in a condition of ]. These relations are derived from ] under the principle of ] (in the absence of external ]s). Given a set of extensive parameters {{math| ''X{{sub|i}}'' }} (energy, mass, entropy, number of particles and so on) and ] {{math| ''F{{sub|i}}'' }} (related to their related intrinsic parameters, such as temperature and pressure), the Onsager theorem states that<ref name=":0"/> | |||
| {{main|Combined law of thermodynamics}} | |||
| : <math> \frac{\mathrm dJ_k }{ \mathrm{d} F_i } \bigg|_{F_i=0} ~=~ \frac{ \mathrm{d} J_i }{ \mathrm{d} F_k } \bigg|_{F_k=0} </math> | |||
| Aside from the established four basic laws of thermodynamics described above, there is also the '''combined law of thermodynamics'''. The combined law of thermodynamics is essentially the first and second laws subsumed into the following single concise mathematical statement:<ref> - Wolfram's World of Science</ref><ref>{{cite book | author=Lehninger, Albert, L. | title=Bioenergetics, 2nd Ed. | year=1973 | id=ISBN 0-8053-6103-0}}</ref> | |||
| where {{math|''i'', ''k'' {{=}} 1,2,3,...}} index every parameter and its related force, and | |||
| :<math> |
: <math>J_i = \frac{\mathrm dX_i }{ \mathrm dt }</math> | ||
| are called the thermodynamic flows. | |||
| Here, E is ], T is ], S is ], p is ], and V is ]. | |||
| == Tentative fourth laws or principles == | |||
| In the late 19th century, thermodynamicist ] argued that the fundamental object of contention in the life-struggle in the evolution of the organic world is 'available energy'. Since then, over the years, various thermodynamic researchers have come forward to ascribe to or to postulate potential '''fourth laws of thermodynamics'''; in some cases, even fifth or sixth laws of thermodynamics are proposed. The majority of these tentative fourth law statements are attempts to apply ] to ]. Most fourth law statements, however, are speculative and far from agreed upon. | |||
| The most commonly proposed Fourth Law is the ]. Another example is the ] as put forward initially by biologist ] in his 1922 article ''Contributions to the Energetics of Evolution''.<ref>A.J.Lotka (1922a) '' . Proc Natl Acad Sci, 8: pp. 147–51.</ref> Most variations of hypothetical fourth laws (or principles) have to do with the environmental sciences, biological evolution, or galactic phenomena.<ref>Morel, R.E. ,Fleck, George. (2006). "" ''Chemistry, Vol. 15'', Iss. 4</ref> | |||
| == Extended interpretations == | |||
| The laws of thermodynamics are sometimes interpreted to have a wider significance and implication than simply encoding the experimental results upon which the science of thermodynamics is based. See, for example: | |||
| * ] | |||
| * ] | |||
| == See also == | == See also == | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] (Parody of the laws of thermodynamics) | |||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | |||
| == References == | == References == | ||
| {{reflist}} | {{reflist|30em}} | ||
| ==Further reading== | == Further reading == | ||
| * |
* ] (2007). ''Four Laws That Drive the Universe''. OUP Oxford. {{ISBN|978-0199232369}} | ||
| * Goldstein, Martin & Inge F. (1993). ''The Refrigerator and the Universe''. Harvard Univ. Press. {{ISBN|978-0674753259}} | |||
| * Guggenheim, E.A. (1985). ''Thermodynamics. An Advanced Treatment for Chemists and Physicists'', seventh edition. {{ISBN|0-444-86951-4}} | |||
| * Adkins, C. J., (1968) ''Equilibrium Thermodynamics''. McGraw-Hill {{ISBN|0-07-084057-1}} | |||
| == External links == | == External links == | ||
| * {{Commonscatinline}} | |||
| * | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 21:11, 23 December 2024
Observational basis of thermodynamics| Thermodynamics | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 The classical Carnot heat engine The classical Carnot heat engine | |||||||||||||||||||||
| Branches | |||||||||||||||||||||
| Laws | |||||||||||||||||||||
Systems
|
|||||||||||||||||||||
System propertiesNote: Conjugate variables in italics
|
|||||||||||||||||||||
Material properties
|
|||||||||||||||||||||
| Equations | |||||||||||||||||||||
| Potentials | |||||||||||||||||||||
|
|||||||||||||||||||||
| Scientists | |||||||||||||||||||||
| Other | |||||||||||||||||||||
The laws of thermodynamics are a set of scientific laws which define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general and are applicable in other natural sciences.
Traditionally, thermodynamics has recognized three fundamental laws, simply named by an ordinal identification, the first law, the second law, and the third law. A more fundamental statement was later labelled as the zeroth law after the first three laws had been established.
The zeroth law of thermodynamics defines thermal equilibrium and forms a basis for the definition of temperature: if two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.
The first law of thermodynamics states that, when energy passes into or out of a system (as work, heat, or matter), the system's internal energy changes in accordance with the law of conservation of energy.
The second law of thermodynamics states that in a natural thermodynamic process, the sum of the entropies of the interacting thermodynamic systems never decreases. A common corollary of the statement is that heat does not spontaneously pass from a colder body to a warmer body.
The third law of thermodynamics states that a system's entropy approaches a constant value as the temperature approaches absolute zero. With the exception of non-crystalline solids (glasses), the entropy of a system at absolute zero is typically close to zero.
The first and second laws prohibit two kinds of perpetual motion machines, respectively: the perpetual motion machine of the first kind which produces work with no energy input, and the perpetual motion machine of the second kind which spontaneously converts thermal energy into mechanical work.
History
Main article: History of thermodynamics See also: Timeline of thermodynamicsThe history of thermodynamics is fundamentally interwoven with the history of physics and the history of chemistry, and ultimately dates back to theories of heat in antiquity. The laws of thermodynamics are the result of progress made in this field over the nineteenth and early twentieth centuries. The first established thermodynamic principle, which eventually became the second law of thermodynamics, was formulated by Sadi Carnot in 1824 in his book Reflections on the Motive Power of Fire. By 1860, as formalized in the works of scientists such as Rudolf Clausius and William Thomson, what are now known as the first and second laws were established. Later, Nernst's theorem (or Nernst's postulate), which is now known as the third law, was formulated by Walther Nernst over the period 1906–1912. While the numbering of the laws is universal today, various textbooks throughout the 20th century have numbered the laws differently. In some fields, the second law was considered to deal with the efficiency of heat engines only, whereas what was called the third law dealt with entropy increases. Gradually, this resolved itself and a zeroth law was later added to allow for a self-consistent definition of temperature. Additional laws have been suggested, but have not achieved the generality of the four accepted laws, and are generally not discussed in standard textbooks.
Zeroth law
The zeroth law of thermodynamics provides for the foundation of temperature as an empirical parameter in thermodynamic systems and establishes the transitive relation between the temperatures of multiple bodies in thermal equilibrium. The law may be stated in the following form:
If two systems are both in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.
Though this version of the law is one of the most commonly stated versions, it is only one of a diversity of statements that are labeled as "the zeroth law". Some statements go further, so as to supply the important physical fact that temperature is one-dimensional and that one can conceptually arrange bodies in a real number sequence from colder to hotter.
These concepts of temperature and of thermal equilibrium are fundamental to thermodynamics and were clearly stated in the nineteenth century. The name 'zeroth law' was invented by Ralph H. Fowler in the 1930s, long after the first, second, and third laws were widely recognized. The law allows the definition of temperature in a non-circular way without reference to entropy, its conjugate variable. Such a temperature definition is said to be 'empirical'.
First law
See also: Thermodynamic cycleThe first law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic processes. In general, the conservation law states that the total energy of an isolated system is constant; energy can be transformed from one form to another, but can be neither created nor destroyed.
In a closed system (i.e. there is no transfer of matter into or out of the system), the first law states that the change in internal energy of the system (ΔUsystem) is equal to the difference between the heat supplied to the system (Q) and the work (W) done by the system on its surroundings. (Note, an alternate sign convention, not used in this article, is to define W as the work done on the system by its surroundings):
For processes that include the transfer of matter, a further statement is needed.
When two initially isolated systems are combined into a new system, then the total internal energy of the new system, Usystem, will be equal to the sum of the internal energies of the two initial systems, U1 and U2:
The First Law encompasses several principles:
- Conservation of energy, which says that energy can be neither created nor destroyed, but can only change form. A particular consequence of this is that the total energy of an isolated system does not change.
- The concept of internal energy and its relationship to temperature. If a system has a definite temperature, then its total energy has three distinguishable components, termed kinetic energy (energy due to the motion of the system as a whole), potential energy (energy resulting from an externally imposed force field), and internal energy. The establishment of the concept of internal energy distinguishes the first law of thermodynamics from the more general law of conservation of energy.
- Work is a process of transferring energy to or from a system in ways that can be described by macroscopic mechanical forces acting between the system and its surroundings. The work done by the system can come from its overall kinetic energy, from its overall potential energy, or from its internal energy. For example, when a machine (not a part of the system) lifts a system upwards, some energy is transferred from the machine to the system. The system's energy increases as work is done on the system and in this particular case, the energy increase of the system is manifested as an increase in the system's gravitational potential energy. Work added to the system increases the potential energy of the system.
- When matter is transferred into a system, the internal energy and potential energy associated with it are transferred into the new combined system. where u denotes the internal energy per unit mass of the transferred matter, as measured while in the surroundings; and ΔM denotes the amount of transferred mass.
- The flow of heat is a form of energy transfer. Heat transfer is the natural process of moving energy to or from a system, other than by work or the transfer of matter. In a diathermal system, the internal energy can only be changed by the transfer of energy as heat:
Combining these principles leads to one traditional statement of the first law of thermodynamics: it is not possible to construct a machine which will perpetually output work without an equal amount of energy input to that machine. Or more briefly, a perpetual motion machine of the first kind is impossible.
Second law
The second law of thermodynamics indicates the irreversibility of natural processes, and in many cases, the tendency of natural processes to lead towards spatial homogeneity of matter and energy, especially of temperature. It can be formulated in a variety of interesting and important ways. One of the simplest is the Clausius statement, that heat does not spontaneously pass from a colder to a hotter body.
It implies the existence of a quantity called the entropy of a thermodynamic system. In terms of this quantity it implies that
When two initially isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium with itself but not necessarily with each other, are then allowed to interact, they will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initially isolated systems is less than or equal to the total entropy of the final combination. Equality occurs just when the two original systems have all their respective intensive variables (temperature, pressure) equal; then the final system also has the same values.
The second law is applicable to a wide variety of processes, both reversible and irreversible. According to the second law, in a reversible heat transfer, an element of heat transferred, , is the product of the temperature (), both of the system and of the sources or destination of the heat, with the increment () of the system's conjugate variable, its entropy ():
While reversible processes are a useful and convenient theoretical limiting case, all natural processes are irreversible. A prime example of this irreversibility is the transfer of heat by conduction or radiation. It was known long before the discovery of the notion of entropy that when two bodies, initially of different temperatures, come into direct thermal connection, then heat immediately and spontaneously flows from the hotter body to the colder one.
Entropy may also be viewed as a physical measure concerning the microscopic details of the motion and configuration of a system, when only the macroscopic states are known. Such details are often referred to as disorder on a microscopic or molecular scale, and less often as dispersal of energy. For two given macroscopically specified states of a system, there is a mathematically defined quantity called the 'difference of information entropy between them'. This defines how much additional microscopic physical information is needed to specify one of the macroscopically specified states, given the macroscopic specification of the other – often a conveniently chosen reference state which may be presupposed to exist rather than explicitly stated. A final condition of a natural process always contains microscopically specifiable effects which are not fully and exactly predictable from the macroscopic specification of the initial condition of the process. This is why entropy increases in natural processes – the increase tells how much extra microscopic information is needed to distinguish the initial macroscopically specified state from the final macroscopically specified state. Equivalently, in a thermodynamic process, energy spreads.
Third law
The third law of thermodynamics can be stated as:
A system's entropy approaches a constant value as its temperature approaches absolute zero.
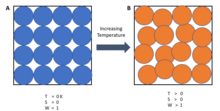
At absolute zero temperature, the system is in the state with the minimum thermal energy, the ground state. The constant value (not necessarily zero) of entropy at this point is called the residual entropy of the system. With the exception of non-crystalline solids (e.g. glass) the residual entropy of a system is typically close to zero. However, it reaches zero only when the system has a unique ground state (i.e., the state with the minimum thermal energy has only one configuration, or microstate). Microstates are used here to describe the probability of a system being in a specific state, as each microstate is assumed to have the same probability of occurring, so macroscopic states with fewer microstates are less probable. In general, entropy is related to the number of possible microstates according to the Boltzmann principle
where S is the entropy of the system, kB is the Boltzmann constant, and Ω the number of microstates. At absolute zero there is only 1 microstate possible (Ω = 1 as all the atoms are identical for a pure substance, and as a result all orders are identical as there is only one combination) and .
Onsager relations
The Onsager reciprocal relations have been considered the fourth law of thermodynamics. They describe the relation between thermodynamic flows and forces in non-equilibrium thermodynamics, under the assumption that thermodynamic variables can be defined locally in a condition of local equilibrium. These relations are derived from statistical mechanics under the principle of microscopic reversibility (in the absence of external magnetic fields). Given a set of extensive parameters Xi (energy, mass, entropy, number of particles and so on) and thermodynamic forces Fi (related to their related intrinsic parameters, such as temperature and pressure), the Onsager theorem states that
where i, k = 1,2,3,... index every parameter and its related force, and
are called the thermodynamic flows.
See also
- Chemical thermodynamics
- Enthalpy
- Entropy production
- Ginsberg's theorem (Parody of the laws of thermodynamics)
- H-theorem
- Statistical mechanics
- Table of thermodynamic equations
References
- ^ Guggenheim, E.A. (1985). Thermodynamics. An Advanced Treatment for Chemists and Physicists, seventh edition, North Holland, Amsterdam, ISBN 0-444-86951-4.
- ^ Kittel, C. Kroemer, H. (1980). Thermal Physics, second edition, W.H. Freeman, San Francisco, ISBN 0-7167-1088-9.
- Adkins, C.J. (1968). Equilibrium Thermodynamics, McGraw-Hill, London, ISBN 0-07-084057-1.
- Guggenheim (1985), p. 8.
- Sommerfeld, A. (1951/1955). Thermodynamics and Statistical Mechanics, vol. 5 of Lectures on Theoretical Physics, edited by F. Bopp, J. Meixner, translated by J. Kestin, Academic Press, New York, p. 1.
- Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pp. 411–51.
- Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pp. 3–32, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
- Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (first edition 1968), third edition 1983, Cambridge University Press, ISBN 0-521-25445-0, pp. 18–20.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 26.
- Buchdahl, H.A. (1966), The Concepts of Classical Thermodynamics, Cambridge University Press, London, pp. 30, 34ff, 46f, 83.
- *Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, p. 22.
- Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge, p. 10.
- Wilson, H.A. (1966). Thermodynamics and Statistical Mechanics, Cambridge University Press, London, pp. 4, 8, 68, 86, 97, 311.
- Ben-Naim, A. (2008). A Farewell to Entropy: Statistical Thermodynamics Based on Information, World Scientific, New Jersey, ISBN 978-981-270-706-2.
- Wendt, Richard P. (1974). "Simplified transport theory for electrolyte solutions". Journal of Chemical Education. 51 (10). American Chemical Society (ACS): 646. Bibcode:1974JChEd..51..646W. doi:10.1021/ed051p646. ISSN 0021-9584.
- ^ Deffner, Sebastian (2019). Quantum thermodynamics : an introduction to the thermodynamics of quantum information. Steve Campbell, Institute of Physics. San Rafael, CA: Morgan & Claypool Publishers. ISBN 978-1-64327-658-8. OCLC 1112388794.
- "Lars Onsager – American chemist". Encyclopaedia Britannica (biography). Retrieved 2021-03-10.
Further reading
- Atkins, Peter (2007). Four Laws That Drive the Universe. OUP Oxford. ISBN 978-0199232369
- Goldstein, Martin & Inge F. (1993). The Refrigerator and the Universe. Harvard Univ. Press. ISBN 978-0674753259
- Guggenheim, E.A. (1985). Thermodynamics. An Advanced Treatment for Chemists and Physicists, seventh edition. ISBN 0-444-86951-4
- Adkins, C. J., (1968) Equilibrium Thermodynamics. McGraw-Hill ISBN 0-07-084057-1
External links
 Media related to Laws of thermodynamics at Wikimedia Commons
Media related to Laws of thermodynamics at Wikimedia Commons


















 where u denotes the internal energy per unit mass of the transferred matter, as measured while in the surroundings; and ΔM denotes the amount of transferred mass.
where u denotes the internal energy per unit mass of the transferred matter, as measured while in the surroundings; and ΔM denotes the amount of transferred mass.
 , is the product of the temperature (
, is the product of the temperature ( ) of the system's conjugate variable, its
) of the system's conjugate variable, its  ):
):


 .
.

