| Revision as of 11:02, 31 January 2015 editDouble sharp (talk | contribs)Autopatrolled, Extended confirmed users, Page movers, File movers, Pending changes reviewers102,065 editsmNo edit summary← Previous edit | Latest revision as of 05:35, 16 December 2024 edit undoCitation bot (talk | contribs)Bots5,439,202 edits Altered pages. Added website. Removed URL that duplicated identifier. Formatted dashes. | Use this bot. Report bugs. | Suggested by Dominic3203 | Linked from User:Mathbot/Most_linked_math_articles | #UCB_webform_linked 944/1913 | ||
| (333 intermediate revisions by 95 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Regular non-convex polygon}} | |||
| {{Distinguish|Star-shaped polygon}} | |||
| {| class="wikitable" align=right | |||
| {| class=wikitable align=right width=320 style="margin: 0px 0px 10px 10px" | |||
| |+ '''Set of regular star polygons''' | |||
| |+ Two types of star pentagons | |||
| |- align=center | |||
| |]<BR>{5/2} | |||
| |]<BR>{{pipe}}5/2{{pipe}} | |||
| |- | |- | ||
| |colspan=2|A regular star ], {5/2}, has five vertices (its corner tips) and five intersecting edges, while a concave ], {{pipe}}5/2{{pipe}}, has ten edges and two sets of five vertices. The first is used in definitions of ] and star ]s, while the second is sometimes used in planar tilings. | |||
| | colspan=2| | |||
| {| class="wikitable" | |||
| |- align=center | |- align=center | ||
| |]< |
|]<BR>] | ||
| |]< |
|]<BR>] | ||
| |]<br>] | |||
| |]<br>] | |||
| |- align=center | |||
| |]<br>] | |||
| |]<br>] | |||
| |]<br>] | |||
| |... | |||
| |} | |||
| |- | |||
| ! ]<br>2<2q<p<br>](p,q)=1 | |||
| |{p/q} | |||
| |- | |||
| ! ] and ] | |||
| |p | |||
| |- | |||
| ! ] | |||
| |q | |||
| |- | |||
| ! ] | |||
| |{{CDD|node_1|p|rat|dq|node}} | |||
| |- | |||
| ! ] | |||
| |] (D<sub>p</sub>) | |||
| |- | |||
| ! ] | |||
| |Self-dual | |||
| |- | |||
| ! ]<br>(]s) | |||
| |<math>\frac{180(p-2q)}{p}</math><ref>{{cite book |last=Kappraff |first=Jay |title=Beyond measure: a guided tour through nature, myth, and number |publisher=World Scientific |year=2002 |page=258 |isbn= 978-981-02-4702-7 |url=http://books.google.com/books?id=vAfBrK678_kC&pg=PA256&dq=star+polygon}}</ref> | |||
| |} | |} | ||
| A regular '''star polygon''' (not to be confused with a ] or a ]) is a ] ] ]. Only the regular star polygons have been studied in any depth; star polygons in general appear not to have been formally defined. | |||
| In ], a '''star polygon''' is a type of non-]. '''Regular star polygons''' have been studied in depth; while star polygons in general appear not to have been formally defined, ] can arise through truncation operations on regular simple or star polygons. | |||
| ==Etymology== | |||
| Modern star-polygon names combine a ], such as '']'', with the ] suffix '']'' (in this case generating the word '']''). The prefix is normally a Greek ], but synonyms using other prefixes exist. For example, a nine-pointed polygon or '']'' is also known as a ''nonagram'', using the ] ''nona'' from ]. | |||
| ] identified two primary usages of this terminology by ], one corresponding to the ]s with ] that do not generate new vertices, and the other one to the ] ] ]s.<ref name=tilingsandpatterns>Grünbaum & Shephard (1987). Tilings and Patterns. Section 2.5</ref> | |||
| Although this prefix+suffix formula can generate or find star-polygon names, it does not necessarily reflect each word's history. For example, ''pentagram'' derives from ''pentagrammos'' / ''pentegrammos'' ("five lines") whose ''-grammos'' derives from ''grammē'' meaning "line". The ''-gram'' suffix, however, derives from ''gramma'' meaning "to write". ''Gramma'' and ''grammē'' do however resemble each other closely in sound, writing (γράμμα, γραμμή) and meaning ("written character, letter, that which is drawn", "stroke or line of a pen,<ref>, Henry George Liddell, Robert Scott, ''A Greek-English Lexicon'', on Perseus</ref>") and are possibly ]s. | |||
| ] include polygons like the ], but also compound figures like the ]. | |||
| ==Regular star polygons== | |||
| In ], a "regular star polygon" is a self-intersecting, equilateral equiangular ], created by connecting one ] of a simple, regular, ''p''-sided polygon to another, non-adjacent vertex and continuing the process until the original vertex is reached again.<ref>{{cite book |last=Coxeter |first=Harold Scott Macdonald |title=Regular polytopes |publisher=Courier Dover Publications |year=1973 |isbn=978-0-486-61480-9}}</ref> Alternatively for integers ''p'' and ''q'', it can be considered as being constructed by connecting every ''q''th point out of ''p'' points regularly spaced in a circular placement.<ref>{{MathWorld |urlname=StarPolygon |title=Star Polygon}}</ref> For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the first to the third vertex, from the third vertex to the fifth vertex, from the fifth vertex to the second vertex, from the second vertex to the fourth vertex, and from the fourth vertex to the first vertex. The notation for such a polygon is {''p''/''q''} (''see ]''), which is equal to {''p''/''p-q''}. Regular star polygons will be produced when ''p'' and ''q'' are ] (they share no factors). A regular star polygon can also be represented as a sequence of ]s of a convex regular ''core'' polygon. Regular star polygons were first studied systematically by ]. | |||
| One definition of a ''star polygon'', used in ], is a polygon having ''q'' ≥ 2 ] (''q'' is called the ] or ]), like in ]s.<ref name="turtle">Abelson, Harold, diSessa, Andera, 1980, ''Turtle Geometry'', MIT Press, p. 24</ref> | |||
| ===Examples=== | |||
| ] | |||
| ==Names== | |||
| ===Star figures===<!--This section is linked from ]--> | |||
| Star polygon names combine a ], such as '']'', with the ] suffix '']'' (in this case generating the word '']''). The prefix is normally a Greek ], but synonyms using other prefixes exist. For example, a nine-pointed polygon or '']'' is also known as a ''nonagram'', using the ] ''nona'' from ].{{citation needed|date=February 2015|reason=Do authoritative sources use both prefixes?}} The ''-gram'' suffix derives from '']'' (''grammḗ''), meaning a line.<ref>, Henry George Liddell, Robert Scott, ''A Greek-English Lexicon'', on Perseus</ref> The name ''star polygon'' reflects the resemblance of these shapes to the ]s of real stars. | |||
| {| class=wikitable align=right | |||
| |+ Small regular polygon compounds | |||
| ==Regular star polygon== | |||
| |- align=center | |||
| {{Further|Regular polygon#Regular star polygons}} | |||
| |]<BR>{6/2}=] | |||
| {| class="wikitable" align=right style="margin: 0px 0px 10px 10px" | |||
| |]<BR>{9/3}=] | |||
| |]<BR> |
|]<BR>] | ||
| |]<BR> |
|]<BR>] | ||
| |]<BR>] | |||
| |- align=center | |||
| |... | |||
| |]<BR>{8/2}=] | |||
| |]<BR>{12/3}=] | |||
| |]<BR>{10/2}=] | |||
| |]<BR>{15/3}=] | |||
| |- align=center | |||
| |]<BR>{12/2}=] | |||
| |]<BR>{14/2}=] | |||
| |]<BR>{16/2}=] | |||
| |]<BR>{18/2}=] | |||
| |} | |} | ||
| ] | |||
| A ''regular star polygon'' is a self-intersecting, equilateral, and equiangular ]. | |||
| A regular star polygon is denoted by its ] {''p''/''q''}, where ''p'' (the number of vertices) and ''q'' (the ]) are ] (they share no factors) and where ''q'' ≥ 2. The density of a polygon can also be called its ]: the sum of the ]s of all the vertices, divided by 360°. | |||
| If the number of sides ''n'' is divisible by ''m'', the star polygon, {''n''/''m''}, obtained will be a regular polygon with ''n''/''m'' sides. A new figure is obtained by rotating these regular ''n''/''m''-gons one vertex to the left on the original polygon until the number of vertices rotated equals ''n''/''m'' minus one, and combining these figures. An extreme case of this is where ''n''/''m'' is 2, producing a figure consisting of ''n''/2 straight line segments; this is called a "] star polygon". | |||
| The ] of {''p''/''q''} is the ] D<sub>''p''</sub>, of order 2''p'', independent of ''q''. | |||
| In other cases where ''n'' and ''m'' have a common factor, a star polygon for a lower ''n'' is obtained, and rotated versions can be combined. These figures are called '''star figures''' or '''improper star polygons''' or '''compound polygons'''. The same notation {''n''/''m''} is often used for them, although authorities such as Grünbaum (1994) regard (with some justification) the form ''k''{''n''} as being more correct, where usually ''k'' = ''m''. | |||
| Regular star polygons were first studied systematically by ], and later ].<ref>Coxeter, Introduction to Geometry, second edition, 2.8 ''Star polygons'', pp. 36–38</ref> | |||
| A further complication comes when we compound two or more star polygons, as for example two pentagrams, differing by a rotation of 36°, inscribed in a decagon. This is correctly written in the form ''k''{''n''/''m''}, as 2{5/2}, rather than the commonly used {10/4}. | |||
| {| class=wikitable | |||
| |+ Small example star polygon compounds | |||
| |- align=center | |||
| |]<BR>{10/4}=] | |||
| |]<BR>{15/6}=] | |||
| |]<BR>{14/4}=] | |||
| |]<BR>{14/6}=] | |||
| |]<BR>{16/6}=] | |||
| |]<BR>{18/4}=] | |||
| |} | |||
| ===Construction via vertex connection=== | |||
| A six-pointed star, like a hexagon, can be created using a compass and a straight edge: | |||
| Regular star polygons can be created by connecting one ] of a regular ''p''-sided simple polygon to another vertex, non-adjacent to the first one, and continuing the process until the original vertex is reached again.<ref>{{cite book |last=Coxeter |first=Harold Scott Macdonald |title=] |publisher=Courier Dover Publications |page= |date=1973 |isbn=978-0-486-61480-9 }}</ref> Alternatively, for integers ''p'' and ''q'', it can be considered as being constructed by connecting every ''q''th point out of ''p'' points regularly spaced in a circular placement.<ref>{{MathWorld |urlname=StarPolygon |title=Star Polygon}}</ref> For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the 1st to the 3rd vertex, from the 3rd to the 5th vertex, from the 5th to the 2nd vertex, from the 2nd to the 4th vertex, and from the 4th to the 1st vertex. | |||
| *Make a circle of any size with the compass. | |||
| *Without changing the radius of the compass, set its pivot on the circle's circumference, and find one of the two points where a new circle would intersect the first circle. | |||
| *With the pivot on the last point found, similarly find a third point on the circumference, and repeat until six such points have been marked. | |||
| *With a straight edge, join alternate points on the circumference to form two overlapping equilateral triangles. | |||
| If ''q'' ≥ ''p''/2, then the construction of {''p''/''q''} will result in the same polygon as {''p''/(''p'' − ''q'')}; connecting every third vertex of the pentagon will yield an identical result to that of connecting every second vertex. However, the vertices will be reached in the opposite direction, which makes a difference when retrograde polygons are incorporated in higher-dimensional polytopes. For example, an ] formed from a prograde pentagram {5/2} results in a ]; the analogous construction from a retrograde "crossed pentagram" {5/3} results in a ]. Another example is the ], which can be seen as a "crossed triangle" {3/2} ]. | |||
| ===Symmetry=== | |||
| Regular star polygons and star figures can be thought of as diagramming ]s of the ]s <math>x\mathbb{Z}_n</math> of the ] <math>\mathbb{Z}_n</math>. | |||
| ====Degenerate regular star polygons==== | |||
| The ] of {''n''/''k''} is ] ''D''<sub>n</sub> of order 2''n'', independent of ''k''. | |||
| If ''p'' and ''q'' are not coprime, a degenerate polygon will result with coinciding vertices and edges. For example, {6/2} will appear as a triangle, but can be labeled with two sets of vertices: 1-3 and 4-6. This should be seen not as two overlapping triangles, but as a double-winding single unicursal hexagon.<ref> {{Webarchive|url=https://web.archive.org/web/20160803160413/http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf |date=2016-08-03 }}, Branko Grünbaum</ref><ref>Coxeter, The Densities of the Regular Polytopes I, p. 43:<BR>If ''q'' is odd, the truncation of {''p''/''q''} is naturally {2''p''/''q''}. But if ''q'' is even, the truncation of {''p''/''q''} consists of two coincident {{nowrap|{''p''/(''q''/2)}'s;}} two, because each side arises once from an original side and once from an original vertex. Since {{nowrap|2(''q''/2) {{=}} ''q'',}} the density of a polygon is never altered by truncation.</ref> | |||
| {{-}} | |||
| :] | |||
| ===Construction via stellation=== | |||
| ==Irregular star polygons== | |||
| Alternatively, a regular star polygon can also be obtained as a sequence of ]s of a convex regular ''core'' polygon. Constructions based on stellation also allow regular polygonal compounds to be obtained in cases where the density ''q'' and amount ''p'' of vertices are not coprime. When constructing star polygons from stellation, however, if ''q'' > ''p''/2, the lines will instead diverge infinitely, and if ''q'' = ''p''/2, the lines will be parallel, with both resulting in no further intersection in Euclidean space. However, it may be possible to construct some such polygons in spherical space, similarly to the ] and ]; such polygons do not yet appear to have been studied in detail. | |||
| ] for the ]. The edge lengths are defined by the distance between alternate vertices in the faces of the ].]] | |||
| A star polygon need not be regular. Irregular ] star polygons occur as ] figures for the ], defined by the sequence of regular polygon faces around each vertex, allowing for both multiple turns, and retrograde directions. (See vertex figures at ])<ref>], ], ], ''Uniform polyhedra'', Phil. Trans. 1954 (Tables 6-8)</ref> | |||
| ==Isotoxal star simple polygons== | |||
| The ] can be seen as a polyhedron with irregular {9/4} star polygon faces with Dih<sub>3</sub> ]. | |||
| When the intersecting line segments are removed from a regular star ''n''-gon, the resulting figure is no longer regular, but can be seen as an ] ] ] '''2'''''n''-gon, alternating vertices at two different radii. ], in '']'', represents such a star that matches the outline of a regular ] {''n''/''d''} as |''n''/''d''|, or more generally with {''n''<sub>𝛼</sub>}, which denotes an ] simple '''2'''''n''-gon with outer ] 𝛼. | |||
| :] | |||
| * For |''n''/''d''|, the outer internal angle {{nowrap|𝛼 {{=}} 180(1 − 2''d''/''n'')}} degrees, necessarily, and the inner (new) vertices have an ] {{nowrap|''β''{{sub|ext}} {{=}} 180}} degrees, necessarily. | |||
| * For {''n''<sub>𝛼</sub>}, the outer internal and inner external angles, also denoted by 𝛼 and ''β''{{sub|ext}}, do not have to match those of any regular polygram {''n''/''d''}; however, {{nowrap|𝛼 < 180(1 − 2/''n'')}} degrees and {{nowrap|''β''{{sub|ext}} < 180°,}} necessarily (here, {''n''<sub>𝛼</sub>} is concave).<ref name=tilingsandpatterns/> | |||
| {| class=wikitable | |||
| |+ Examples of isotoxal star simple polygons | |||
| |- valign=top align=center | |||
| !{{pipe}}''n''/''d''{{pipe}}<BR>{''n''<sub>𝛼</sub>} | |||
| !{{pipe}}9/4{{pipe}}<BR>{9<sub>20°</sub>} | |||
| ! <BR>{3<sub>30°</sub>} | |||
| ! <BR>{6<sub>30°</sub>} | |||
| !{{pipe}}5/2{{pipe}}<BR>{5<sub>36°</sub>} | |||
| ! <BR>{4<sub>45°</sub>} | |||
| !{{pipe}}8/3{{pipe}}<BR>{8<sub>45°</sub>} | |||
| !{{pipe}}6/2{{pipe}}<BR>{6<sub>60°</sub>} | |||
| ! <BR>{5<sub>72°</sub>} | |||
| |- | |||
| !𝛼 | |||
| !20° | |||
| !colspan=2|30° | |||
| !36° | |||
| !colspan=2|45° | |||
| !60° | |||
| !72° | |||
| |- | |||
| !''β''{{sub|ext}} | |||
| !60° | |||
| !150° | |||
| !90° | |||
| !108° | |||
| !135° | |||
| !90° | |||
| !120° | |||
| !144° | |||
| |- valign=top align=center | |||
| !valign=center|Isotoxal<BR>simple<BR>''n''-pointed<BR>star | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |- valign=top align=center | |||
| !valign=center|Related<BR>regular<BR>polygram<BR>{''n''/''d''} | |||
| |]<BR>{9/4} | |||
| |colspan=2|]<BR>{12/5} | |||
| |]<BR>{5/2} | |||
| |colspan=2|]<BR>{8/3} | |||
| |]<BR>2{3}<BR>] | |||
| |]<BR>{10/3} | |||
| |} | |||
| ===Examples in tilings=== | |||
| The ] is another example of a cyclic irregular star polygon, containing Dih<sub>2</sub> ]. | |||
| {{See|Uniform tiling#Uniform tilings using star polygons as concave alternating faces}} | |||
| : ] | |||
| These polygons are often seen in tiling patterns. The parametric angle 𝛼 (in degrees or radians) can be chosen to match ]s of neighboring polygons in a tessellation pattern. In his 1619 work '']'', among periodic tilings, ] includes nonperiodic tilings, like that with three regular pentagons and one regular star pentagon fitting around certain vertices, 5.5.5.5/2, and related to modern ]s.<ref name="maa.org"></ref> | |||
| {| class="wikitable nowrap" | |||
| |+ Examples of isogonal tilings with isotoxal simple stars<ref>, Joseph Myers</ref> | |||
| !valign=center|Isotoxal simple<BR>''n''-pointed stars | |||
| !"Triangular" stars<BR>(''n'' = 3) | |||
| !"Square" stars<BR>(''n'' = 4) | |||
| !colspan=3|"Hexagonal" stars<BR>(''n'' = 6) | |||
| !"Octagonal" stars<BR>(''n'' = 8) | |||
| |- align=center valign=center | |||
| !Image of tiling | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |] | |||
| |- align=center valign=center | |||
| !Vertex config. | |||
| |3.3{{supsub|*|𝛼}}.3.3{{supsub|**|𝛼}} | |||
| |8.4{{supsub|*|π/4}}.8.4{{supsub|*|π/4}} | |||
| |6.6{{supsub|*|π/3}}.6.6{{supsub|*|π/3}} | |||
| |3.6{{supsub|*|π/3}}.6{{supsub|**|π/3}} | |||
| |3.6.6{{supsub|*|π/3}}.6 | |||
| |not edge-to-edge | |||
| |} | |||
| ==Interiors |
==Interiors== | ||
| The interior of a star polygon may be treated in different ways. Three such treatments are illustrated for a pentagram. ] and Geoffrey Shephard consider two of them, as regular star ''n''-gons and as isotoxal concave simple '''2'''''n''-gons.<ref name="maa.org"/> | |||
| Star polygons leave an ambiguity of interpretation for interiors. This diagram demonstrates three ''interpretations'' of a pentagram. | |||
| ] | ] | ||
| *The left-hand interpretation has the 5 vertices of a regular pentagon connected alternately on a cyclic path, skipping alternate vertices. The interior is everything immediately left (or right) from each edge (until the next intersection). This makes the core convex pentagonal region actually "outside", and in general you can determine inside by a binary ] of counting how many edges are intersected from a point along a ray to infinity. | |||
| *The middle interpretation also has the 5 vertices of a regular pentagon connected alternately on a cyclic path. The interior may be treated either: | |||
| **as the inside of a simple 10-sided polygon perimeter boundary, as below. | |||
| **with the central convex pentagonal region surrounded twice, because the starry perimeter winds around it twice. | |||
| *The right-hand interpretation creates new vertices at the intersections of the edges (5 in this case) and defines a new concave decagon (10-pointed polygon) formed by perimeter path of the middle interpretation; it is in fact no longer a pentagram. | |||
| These three treatments are: | |||
| What is the area inside the pentagram? Each interpretation leads to a ]. | |||
| * Where a line segment occurs, one side is treated as outside and the other as inside. This is shown in the left hand illustration and commonly occurs in computer ] rendering. | |||
| * The number of times that the polygonal curve winds around a given region determines its '']''. The exterior is given a density of 0, and any region of density > 0 is treated as internal. This is shown in the central illustration and commonly occurs in the mathematical treatment of ]. (However, for non-orientable polyhedra, density can only be considered modulo 2 and hence, in those cases, for consistency, the first treatment is sometimes used instead.) | |||
| * Wherever a line segment may be drawn between two sides, the region in which the line segment lies is treated as inside the figure.<!--This definition of the interior is false for a concave figure, isn't it? Perhaps mentioning the outline of a polygram would help?--> This is shown in the right hand illustration and commonly occurs when making a physical model. | |||
| When the area of the polygon is calculated, each of these approaches yields a different result. | |||
| ===Example interpretations of a star prism=== | |||
| ''']:''' | |||
| {| class="wikitable" | |||
| |]<br>Heptagrams with<br>''2-sided'' interior | |||
| |]<br>Heptagrams with<br>a simple perimeter interior | |||
| |} | |||
| The heptagrammic prism above shows different interpretations can create very different appearances. | |||
| Builders of ]s, like ], usually represent ''star polygon'' faces in the concave form, without ''internal edges'' shown. | |||
| == |
==In art and culture== | ||
| {{Main|Star polygons in art and culture}} | {{Main|Star polygons in art and culture}} | ||
| {{refimprove section|date=March 2024}} | |||
| Star polygons feature prominently in art and culture. Such polygons may or may not be ] but they are always highly ]. Examples include: | Star polygons feature prominently in art and culture. Such polygons may or may not be ], but they are always highly ]. Examples include: | ||
| *The {5/2} star pentagon is also known as a |
* The {5/2} star pentagon (]) is also known as a pentalpha or pentangle, and historically has been considered by many ]al and ] cults to have ] significance. | ||
| * The {7/2} and {7/3} star polygons (]s) also have occult significance, particularly in the ] and in ]. | |||
| *The simplest compound star polygon is two opposed triangles, sometimes written as {6/2} or 2{3} and known variously as the ], (] or ]). | |||
| * The {8/3} star polygon (]) is a frequent geometrical motif in ] ] and ]; the first is on the ]. | |||
| *The {7/3} and {7/2} star polygons which are known as ]s and also have occult significance, particularly in the ] and in ]. | |||
| * An eleven pointed star called the ] was used on the ].<ref>{{Cite book |last=Broug |first=Eric |title=Islamic Geometric Patterns |date=2008-05-27 |publisher=Thames and Hudson |pages=183–185, 193 |isbn=978-0-500-28721-7 |location=London |language=English}}</ref> | |||
| *The compound of two squares, sometimes written as {8/2} or 2{4}, is known in ] as the ] and in ] as the ]. | |||
| *The {8/3} star polygon (]), and the compound {16/6} (or 2{8/3}) are frequent geometrical motifs in ] ] and ]; the first is on the ]. | |||
| *An eleven pointed star called the ] was used on the tomb of Shah Nemat Ollah Vali. | |||
| {| class=wikitable width= |
{| class=wikitable width=300 | ||
| |- valign=top | |- valign=top | ||
| |]<BR>An {8/3} |
|]<BR>An {8/3} ] constructed in a regular ] | ||
| |]<BR>Seal of Solomon |
|]<BR>] with circle and dots (star figure) | ||
| |]<BR>2{4} star figure | |||
| |]<BR>2{8/3} star figure | |||
| |} | |} | ||
| ==See also== | ==See also== | ||
| * ] | |||
| *] | |||
| * ] | |||
| *] | |||
| *] | * ] | ||
| *] | * ] | ||
| * ] | |||
| *] (4-polytopes) | |||
| * ] | |||
| *] | |||
| * ] | |||
| *] | |||
| * ] | |||
| * ], ], and ] | |||
| * ] | |||
| ==References== | ==References== | ||
| {{reflist}} | {{reflist}} | ||
| *Cromwell, P.; ''Polyhedra'', CUP, Hbk. 1997, |
* Cromwell, P.; ''Polyhedra'', CUP, Hbk. 1997, {{isbn|0-521-66432-2}}. Pbk. 1999, {{isbn|0-521-66405-5}}. p. 175 | ||
| *] and G.C. Shephard; ''Tilings and Patterns'', New York: W. H. Freeman & Co. |
* ] and G. C. Shephard; ''Tilings and Patterns'', New York: W. H. Freeman & Co. (1987), {{isbn|0-7167-1193-1}}. | ||
| *Grünbaum, B.; Polyhedra with Hollow Faces, ''Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993)'', ed T. Bisztriczky et al., Kluwer Academic (1994) pp. |
* ]; Polyhedra with Hollow Faces, ''Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto, 1993)'', ed. T. Bisztriczky ''et al.'', Kluwer Academic (1994), pp. 43–70. | ||
| *], Heidi Burgiel, Chaim Goodman- |
* ], Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'', 2008, {{isbn|978-1-56881-220-5}} (Chapter 26, p. 404: Regular star-polytopes Dimension 2) | ||
| * ], ''Metamorphoses of polygons'', published in ''The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History'' (1994) | |||
| ==External |
==External Links== | ||
| {{Cite web|last=Hart|first=Vi|url=http://www.youtube.com/watch?v=CfJzrmS9UfY|title=Doodling in Math Class: Stars|website=] |year=2010}} | |||
| *{{Mathworld |urlname=Polygram |title=Polygram}} | |||
| * | |||
| {{Polygons}} | {{Polygons}} | ||
| {{DEFAULTSORT:Star |
{{DEFAULTSORT:Star polygon}} | ||
| ] | |||
| ] | ] | ||
| ] | |||
Latest revision as of 05:35, 16 December 2024
Regular non-convex polygon Not to be confused with Star-shaped polygon. {5/2} |
 |5/2| |
| A regular star pentagon, {5/2}, has five vertices (its corner tips) and five intersecting edges, while a concave decagon, |5/2|, has ten edges and two sets of five vertices. The first is used in definitions of star polyhedra and star uniform tilings, while the second is sometimes used in planar tilings. | |
 Small stellated dodecahedron |
 Tessellation |
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.
Branko Grünbaum identified two primary usages of this terminology by Johannes Kepler, one corresponding to the regular star polygons with intersecting edges that do not generate new vertices, and the other one to the isotoxal concave simple polygons.
Polygrams include polygons like the pentagram, but also compound figures like the hexagram.
One definition of a star polygon, used in turtle graphics, is a polygon having q ≥ 2 turns (q is called the turning number or density), like in spirolaterals.
Names
Star polygon names combine a numeral prefix, such as penta-, with the Greek suffix -gram (in this case generating the word pentagram). The prefix is normally a Greek cardinal, but synonyms using other prefixes exist. For example, a nine-pointed polygon or enneagram is also known as a nonagram, using the ordinal nona from Latin. The -gram suffix derives from γραμμή (grammḗ), meaning a line. The name star polygon reflects the resemblance of these shapes to the diffraction spikes of real stars.
Regular star polygon
Further information: Regular polygon § Regular star polygons {5/2} |
 {7/2} |
 {7/3} |
... |

A regular star polygon is a self-intersecting, equilateral, and equiangular polygon.
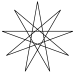
A regular star polygon is denoted by its Schläfli symbol {p/q}, where p (the number of vertices) and q (the density) are relatively prime (they share no factors) and where q ≥ 2. The density of a polygon can also be called its turning number: the sum of the turn angles of all the vertices, divided by 360°.
The symmetry group of {p/q} is the dihedral group Dp, of order 2p, independent of q.
Regular star polygons were first studied systematically by Thomas Bradwardine, and later Johannes Kepler.
Construction via vertex connection
Regular star polygons can be created by connecting one vertex of a regular p-sided simple polygon to another vertex, non-adjacent to the first one, and continuing the process until the original vertex is reached again. Alternatively, for integers p and q, it can be considered as being constructed by connecting every qth point out of p points regularly spaced in a circular placement. For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the 1st to the 3rd vertex, from the 3rd to the 5th vertex, from the 5th to the 2nd vertex, from the 2nd to the 4th vertex, and from the 4th to the 1st vertex.
If q ≥ p/2, then the construction of {p/q} will result in the same polygon as {p/(p − q)}; connecting every third vertex of the pentagon will yield an identical result to that of connecting every second vertex. However, the vertices will be reached in the opposite direction, which makes a difference when retrograde polygons are incorporated in higher-dimensional polytopes. For example, an antiprism formed from a prograde pentagram {5/2} results in a pentagrammic antiprism; the analogous construction from a retrograde "crossed pentagram" {5/3} results in a pentagrammic crossed-antiprism. Another example is the tetrahemihexahedron, which can be seen as a "crossed triangle" {3/2} cuploid.
Degenerate regular star polygons
If p and q are not coprime, a degenerate polygon will result with coinciding vertices and edges. For example, {6/2} will appear as a triangle, but can be labeled with two sets of vertices: 1-3 and 4-6. This should be seen not as two overlapping triangles, but as a double-winding single unicursal hexagon.
Construction via stellation
Alternatively, a regular star polygon can also be obtained as a sequence of stellations of a convex regular core polygon. Constructions based on stellation also allow regular polygonal compounds to be obtained in cases where the density q and amount p of vertices are not coprime. When constructing star polygons from stellation, however, if q > p/2, the lines will instead diverge infinitely, and if q = p/2, the lines will be parallel, with both resulting in no further intersection in Euclidean space. However, it may be possible to construct some such polygons in spherical space, similarly to the monogon and digon; such polygons do not yet appear to have been studied in detail.
Isotoxal star simple polygons
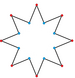
When the intersecting line segments are removed from a regular star n-gon, the resulting figure is no longer regular, but can be seen as an isotoxal concave simple 2n-gon, alternating vertices at two different radii. Branko Grünbaum, in Tilings and patterns, represents such a star that matches the outline of a regular polygram {n/d} as |n/d|, or more generally with {n𝛼}, which denotes an isotoxal concave or convex simple 2n-gon with outer internal angle 𝛼.
- For |n/d|, the outer internal angle 𝛼 = 180(1 − 2d/n) degrees, necessarily, and the inner (new) vertices have an external angle βext = 180 degrees, necessarily.
- For {n𝛼}, the outer internal and inner external angles, also denoted by 𝛼 and βext, do not have to match those of any regular polygram {n/d}; however, 𝛼 < 180(1 − 2/n) degrees and βext < 180°, necessarily (here, {n𝛼} is concave).
| |n/d| {n𝛼} |
|9/4| {920°} |
{330°} |
{630°} |
|5/2| {536°} |
{445°} |
|8/3| {845°} |
|6/2| {660°} |
{572°} |
|---|---|---|---|---|---|---|---|---|
| 𝛼 | 20° | 30° | 36° | 45° | 60° | 72° | ||
| βext | 60° | 150° | 90° | 108° | 135° | 90° | 120° | 144° |
| Isotoxal simple n-pointed star |

|

|

|

|

|
|

|

|
| Related regular polygram {n/d} |
 {9/4} |
 {12/5} |
 {5/2} |
 {8/3} |
 2{3} Star figure |
 {10/3} | ||
Examples in tilings
Further information: Uniform tiling § Uniform tilings using star polygons as concave alternating facesThese polygons are often seen in tiling patterns. The parametric angle 𝛼 (in degrees or radians) can be chosen to match internal angles of neighboring polygons in a tessellation pattern. In his 1619 work Harmonices Mundi, among periodic tilings, Johannes Kepler includes nonperiodic tilings, like that with three regular pentagons and one regular star pentagon fitting around certain vertices, 5.5.5.5/2, and related to modern Penrose tilings.
Interiors
The interior of a star polygon may be treated in different ways. Three such treatments are illustrated for a pentagram. Branko Grünbaum and Geoffrey Shephard consider two of them, as regular star n-gons and as isotoxal concave simple 2n-gons.
These three treatments are:
- Where a line segment occurs, one side is treated as outside and the other as inside. This is shown in the left hand illustration and commonly occurs in computer vector graphics rendering.
- The number of times that the polygonal curve winds around a given region determines its density. The exterior is given a density of 0, and any region of density > 0 is treated as internal. This is shown in the central illustration and commonly occurs in the mathematical treatment of polyhedra. (However, for non-orientable polyhedra, density can only be considered modulo 2 and hence, in those cases, for consistency, the first treatment is sometimes used instead.)
- Wherever a line segment may be drawn between two sides, the region in which the line segment lies is treated as inside the figure. This is shown in the right hand illustration and commonly occurs when making a physical model.
When the area of the polygon is calculated, each of these approaches yields a different result.
In art and culture
Main article: Star polygons in art and culture| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2024) (Learn how and when to remove this message) |
Star polygons feature prominently in art and culture. Such polygons may or may not be regular, but they are always highly symmetrical. Examples include:
- The {5/2} star pentagon (pentagram) is also known as a pentalpha or pentangle, and historically has been considered by many magical and religious cults to have occult significance.
- The {7/2} and {7/3} star polygons (heptagrams) also have occult significance, particularly in the Kabbalah and in Wicca.
- The {8/3} star polygon (octagram) is a frequent geometrical motif in Mughal Islamic art and architecture; the first is on the emblem of Azerbaijan.
- An eleven pointed star called the hendecagram was used on the tomb of Shah Nematollah Vali.
 An {8/3} octagram constructed in a regular octagon |
 Seal of Solomon with circle and dots (star figure) |
See also
- List of regular polytopes and compounds#Stars
- Five-pointed star
- Magic star
- Moravian star
- Pentagramma mirificum
- Regular star 4-polytope
- Rub el Hizb
- Star (glyph)
- Star polyhedron, Kepler–Poinsot polyhedron, and uniform star polyhedron
- Starfish
References
- ^ Grünbaum & Shephard (1987). Tilings and Patterns. Section 2.5
- Abelson, Harold, diSessa, Andera, 1980, Turtle Geometry, MIT Press, p. 24
- γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons, pp. 36–38
- Coxeter, Harold Scott Macdonald (1973). Regular polytopes. Courier Dover Publications. p. 93. ISBN 978-0-486-61480-9.
- Weisstein, Eric W. "Star Polygon". MathWorld.
- Are Your Polyhedra the Same as My Polyhedra? Archived 2016-08-03 at the Wayback Machine, Branko Grünbaum
- Coxeter, The Densities of the Regular Polytopes I, p. 43:
If q is odd, the truncation of {p/q} is naturally {2p/q}. But if q is even, the truncation of {p/q} consists of two coincident {p/(q/2)}'s; two, because each side arises once from an original side and once from an original vertex. Since 2(q/2) = q, the density of a polygon is never altered by truncation. - ^ Branko Grunbaum and Geoffrey C. Shephard, Tilings by Regular Polygons, Mathematics Magazine #50 (1977), pp. 227–247, and #51 (1978), pp. 205–206
- Tiling with Regular Star Polygons, Joseph Myers
- Broug, Eric (2008-05-27). Islamic Geometric Patterns. London: Thames and Hudson. pp. 183–185, 193. ISBN 978-0-500-28721-7.
- Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. 1999, ISBN 0-521-66405-5. p. 175
- Grünbaum, B. and G. C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co. (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto, 1993), ed. T. Bisztriczky et al., Kluwer Academic (1994), pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things, 2008, ISBN 978-1-56881-220-5 (Chapter 26, p. 404: Regular star-polytopes Dimension 2)
- Branko Grünbaum, Metamorphoses of polygons, published in The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History (1994)
External Links
Hart, Vi (2010). "Doodling in Math Class: Stars". YouTube.
| Polygons (List) | |||||||
|---|---|---|---|---|---|---|---|
| Triangles | |||||||
| Quadrilaterals | |||||||
| By number of sides |
| ||||||
| Star polygons | |||||||
| Classes | |||||||







