Misplaced Pages

Latest revision as of 20:21, 24 August 2024

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2019) (Learn how and when to remove this message)

An oblique shock wave is a shock wave that, unlike a normal shock, is inclined with respect to the direction of incoming air. It occurs when a supersonic flow encounters a corner that effectively turns the flow into itself and compresses. The upstream streamlines are uniformly deflected after the shock wave. The most common way to produce an oblique shock wave is to place a wedge into supersonic, compressible flow. Similar to a normal shock wave, the oblique shock wave consists of a very thin region across which nearly discontinuous changes in the thermodynamic properties of a gas occur. While the upstream and downstream flow directions are unchanged across a normal shock, they are different for flow across an oblique shock wave.

It is always possible to convert an oblique shock into a normal shock by a Galilean transformation.

Wave theory

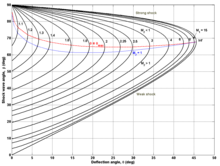
For a given Mach number, M₁, and corner angle, θ, the oblique shock angle, β, and the downstream Mach number, M₂, can be calculated. Unlike after a normal shock where M₂ must always be less than 1, in oblique shock M₂ can be supersonic (weak shock wave) or subsonic (strong shock wave). Weak solutions are often observed in flow geometries open to atmosphere (such as on the outside of a flight vehicle). Strong solutions may be observed in confined geometries (such as inside a nozzle intake). Strong solutions are required when the flow needs to match the downstream high pressure condition. Discontinuous changes also occur in the pressure, density and temperature, which all rise downstream of the oblique shock wave.

The θ-β-M equation

Using the continuity equation and the fact that the tangential velocity component does not change across the shock, trigonometric relations eventually lead to the θ-β-M equation which shows θ as a function of M₁, β and ɣ, where ɣ is the Heat capacity ratio.

${\displaystyle \tan \theta =2\cot \beta \ {\frac {M_{1}^{2}\sin ^{2}\!\beta -1}{M_{1}^{2}(\gamma +\cos 2\beta )+2}}}$

It is more intuitive to want to solve for β as a function of M₁ and θ, but this approach is more complicated, the results of which are often contained in tables or calculated through a numerical method.

Maximum deflection angle

Within the θ-β-M equation, a maximum corner angle, θ_MAX, exists for any upstream Mach number. When θ > θ_MAX, the oblique shock wave is no longer attached to the corner and is replaced by a detached bow shock. A θ-β-M diagram, common in most compressible flow textbooks, shows a series of curves that will indicate θ_MAX for each Mach number. The θ-β-M relationship will produce two β angles for a given θ and M₁, with the larger angle called a strong shock and the smaller called a weak shock. The weak shock is almost always seen experimentally.

The rise in pressure, density, and temperature after an oblique shock can be calculated as follows:

${\displaystyle {\frac {p_{2}}{p_{1}}}=1+{\frac {2\gamma }{\gamma +1}}(M_{1}^{2}\sin ^{2}\!\beta -1)}$

${\displaystyle {\frac {\rho _{2}}{\rho _{1}}}={\frac {(\gamma +1)\ M_{1}^{2}\sin ^{2}\!\beta }{(\gamma -1)M_{1}^{2}\sin ^{2}\!\beta +2}}}$

${\displaystyle {\frac {T_{2}}{T_{1}}}={\frac {p_{2}}{p_{1}}}{\frac {\rho _{1}}{\rho _{2}}}.}$

M₂ is solved for as follows, where ${\displaystyle \theta }$ is the post-shock flow deflection angle:

${\displaystyle M_{2}={\frac {1}{\sin(\beta -\theta )}}{\sqrt {\frac {1+{\frac {\gamma -1}{2}}M_{1}^{2}\sin ^{2}\!\beta }{\gamma M_{1}^{2}\sin ^{2}\!\beta -{\frac {\gamma -1}{2}}}}}.}$

Wave applications

Oblique shocks are often preferable in engineering applications when compared to normal shocks. This can be attributed to the fact that using one or a combination of oblique shock waves results in more favourable post-shock conditions (smaller increase in entropy, less stagnation pressure loss, etc.) when compared to utilizing a single normal shock. An example of this technique can be seen in the design of supersonic aircraft engine intakes or supersonic inlets. A type of these inlets is wedge-shaped to compress air flow into the combustion chamber while minimizing thermodynamic losses. Early supersonic aircraft jet engine intakes were designed using compression from a single normal shock, but this approach caps the maximum achievable Mach number to roughly 1.6. Concorde (which first flew in 1969) used variable geometry wedge-shaped intakes to achieve a maximum speed of Mach 2.2. A similar design was used on the F-14 Tomcat (the F-14D was first delivered in 1994) and achieved a maximum speed of Mach 2.34.

Many supersonic aircraft wings are designed around a thin diamond shape. Placing a diamond-shaped object at an angle of attack relative to the supersonic flow streamlines will result in two oblique shocks propagating from the front tip over the top and bottom of the wing, with Prandtl-Meyer expansion fans created at the two corners of the diamond closest to the front tip. When correctly designed, this generates lift.

Waves and the hypersonic limit

As the Mach number of the upstream flow becomes increasingly hypersonic, the equations for the pressure, density, and temperature after the oblique shock wave reach a mathematical limit. The pressure and density ratios can then be expressed as:

${\displaystyle {\frac {p_{2}}{p_{1}}}\approx {\frac {2\gamma }{\gamma +1}}\ M_{1}^{2}\sin ^{2}\!\beta }$

${\displaystyle {\frac {\rho _{2}}{\rho _{1}}}\approx {\frac {\gamma +1}{\gamma -1}}.}$

For a perfect atmospheric gas approximation using γ = 1.4, the hypersonic limit for the density ratio is 6. However, hypersonic post-shock dissociation of O₂ and N₂ into O and N lowers γ, allowing for higher density ratios in nature. The hypersonic temperature ratio is:

${\displaystyle {\frac {T_{2}}{T_{1}}}\approx {\frac {2\gamma \ (\gamma -1)}{(\gamma +1)^{2}}}\ M_{1}^{2}\sin ^{2}\!\beta .}$

See also

• Bow shock (aerodynamics)
• Gas dynamics
• Mach reflection
• Moving shock
• Shock polar
• Shock wave

References

1. Hall, Nancy (13 May 2021). "Oblique Shock Waves". NASA. Retrieved 9 June 2024.
2. "Archived copy" (PDF). Archived from the original (PDF) on 2012-10-21. Retrieved 2013-01-01.{{cite web}}: CS1 maint: archived copy as title (link)

• Anderson, John D. Jr. (January 2001) . Fundamentals of Aerodynamics (3rd ed.). McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-237335-6.
• Liepmann, Hans W.; Roshko, A. (2001) . Elements of Gasdynamics. Dover Publications. ISBN 978-0-486-41963-3.
• Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0.

External links

• NASA oblique shock wave calculator Archived 2011-07-18 at the Wayback Machine (Java applet)
• Supersonic wind tunnel test demonstration (Mach 2.5) with flat plate and wedge creating an oblique shock(Video)

• Aerodynamics
• Fluid dynamics
• Shock waves