| Revision as of 13:25, 6 February 2022 editHairy Dude (talk | contribs)Extended confirmed users86,662 edits →Van der Grinten IV Projection: capitalisationTags: Mobile edit Mobile web edit Advanced mobile edit← Previous edit | Revision as of 05:42, 26 February 2022 edit undoInternetArchiveBot (talk | contribs)Bots, Pending changes reviewers5,386,731 edits Rescuing 1 sources and tagging 0 as dead.) #IABot (v2.0.8.6) (Whoop whoop pull up - 9541Next edit → | ||
| Line 8: | Line 8: | ||
| == Geometric construction== | == Geometric construction== | ||
| The geometric construction given by van der Grinten can be written algebraically:<ref>, ] Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.</ref> | The geometric construction given by van der Grinten can be written algebraically:<ref> {{Webarchive|url=https://web.archive.org/web/20100701103721/http://pubs.er.usgs.gov/usgspubs/pp/pp1395 |date=2010-07-01 }}, ] Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.</ref> | ||
| <math display="block">\begin{align} | <math display="block">\begin{align} | ||
Revision as of 05:42, 26 February 2022
Compromise map projection
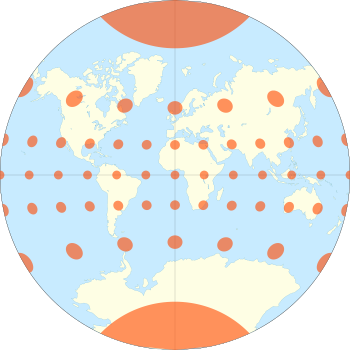
The van der Grinten projection is a compromise map projection, which means that it is neither equal-area nor conformal. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der Grinten projects the entire Earth into a circle. It largely preserves the familiar shapes of the Mercator projection while modestly reducing Mercator's distortion. Polar regions are subject to extreme distortion. Lines of longitude converge to points at the poles.
History
Alphons J. van der Grinten invented the projection in 1898 and received US patent #751,226 for it and three others in 1904. The National Geographic Society adopted the projection for their reference maps of the world in 1922, raising its visibility and stimulating its adoption elsewhere. In 1988, National Geographic replaced the van der Grinten projection with the Robinson projection.
Geometric construction
The geometric construction given by van der Grinten can be written algebraically:
where x takes the sign of λ − λ0, y takes the sign of φ, and
If φ = 0, then
Similarly, if λ = λ0 or φ = ±π/2, then
In all cases, φ is the latitude, λ is the longitude, and λ0 is the central meridian of the projection.
Van der Grinten IV Projection
The van der Grinten IV projection is a later polyconic map projection developed by Alphons J. van der Grinten. The central meridian and equator are straight lines. All other meridians and parallels are arcs of circles.
See also
- List of map projections
- Robinson projection (successor)
References
- ^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 258–262, ISBN 0-226-76747-7.
- A Bibliography of Map Projections, John P. Snyder and Harry Steward, 1989, p. 94, US Geological Survey Bulletin 1856.
- Map Projections – A Working Manual Archived 2010-07-01 at the Wayback Machine, USGS Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.
- "Van der Grinten IV Projection".
- "An Album of Map Projections". p. 205.
- "van der Grinten IV".
Bibliography
External links
This cartography or mapping term article is a stub. You can help Misplaced Pages by expanding it. |



