| Revision as of 23:57, 28 December 2024 editAnomieBOT (talk | contribs)Bots6,574,403 editsm Dating maintenance tags: {{Cn}}← Previous edit | Revision as of 03:32, 29 December 2024 edit undoJohnjbarton (talk | contribs)Extended confirmed users12,318 edits →Hoek experiment: Move the secondary ref which contains a detailed analysis of Hoek's work to the end of the paragraph. Add Whittaker. Move the Hammar expr to See also.Next edit → | ||
| Line 57: | Line 57: | ||
| In 1870 Wilhelm Veltmann demonstrated that Fresnel's formula worked for different frequencies (colors) of light. According the Fresnel's model this would imply different amounts of eather drag for different colors of light. The velocity with white light, a mixture of colors, would be unexplained.<ref name=Stachel2005 group=S/> | In 1870 Wilhelm Veltmann demonstrated that Fresnel's formula worked for different frequencies (colors) of light. According the Fresnel's model this would imply different amounts of eather drag for different colors of light. The velocity with white light, a mixture of colors, would be unexplained.<ref name=Stachel2005 group=S/> | ||
| === Hoek experiment === | === Hoek experiment === | ||
| {{See also|Hammar experiment}} | |||
| An indirect confirmation of Fresnel's dragging coefficient was provided by ] (1868).<ref group=P name=hoek |
An indirect confirmation of Fresnel's dragging coefficient was provided by ] (1868).<ref group=P name=hoek /> | ||
| His apparatus was similar to Fizeau's, though in his version only one arm contained an area filled with resting water, while the other arm was in the air. |
His apparatus was similar to Fizeau's, though in his version only one arm contained an area filled with resting water, while the other arm was in the air. As seen by an observer resting in the aether, Earth and hence the water is in motion. So the following travel times of two light rays traveling in opposite directions were calculated by Hoek (neglecting the transverse direction, see image): | ||
| {|align=center | {|align=center | ||
| Line 69: | Line 70: | ||
| |} | |} | ||
| The travel times are not the same, which should be indicated by an interference shift. However, if Fresnel's dragging coefficient is applied to the water in the aether frame, the travel time difference (to first order in ''v/c'') vanishes. |
The travel times are not the same, which should be indicated by an interference shift. However, if Fresnel's dragging coefficient is applied to the water in the aether frame, the travel time difference (to first order in ''v/c'') vanishes. Upon turning the apparatus table 180 degrees, altering the direction of a hypothetical aether wind, Hoek obtained a null result, confirming Fresnel's dragging coefficient.<ref group=S name=ferr /><ref group=S name=Whittaker/>{{rp|111}} | ||
| In the particular version of the experiment shown here, Hoek used a prism ''P'' to disperse light from a slit into a spectrum which passed through a collimator ''C'' before entering the apparatus. With the apparatus oriented parallel to the hypothetical aether wind, Hoek expected the light in one circuit to be retarded 7/600 mm with respect to the other. Where this retardation represented an integral number of wavelengths, he expected to see constructive interference; where this retardation represented a half-integral number of wavelengths, he expected to see destructive interference. In the absence of dragging, his expectation was for the observed spectrum to be continuous with the apparatus oriented transversely to the aether wind, and to be banded with the apparatus oriented parallel to the aether wind. His actual experimental results were completely negative.<ref group=P name=hoek /><ref group=S name=ferr /> | In the particular version of the experiment shown here, Hoek used a prism ''P'' to disperse light from a slit into a spectrum which passed through a collimator ''C'' before entering the apparatus. With the apparatus oriented parallel to the hypothetical aether wind, Hoek expected the light in one circuit to be retarded 7/600 mm with respect to the other. Where this retardation represented an integral number of wavelengths, he expected to see constructive interference; where this retardation represented a half-integral number of wavelengths, he expected to see destructive interference. In the absence of dragging, his expectation was for the observed spectrum to be continuous with the apparatus oriented transversely to the aether wind, and to be banded with the apparatus oriented parallel to the aether wind. His actual experimental results were completely negative.<ref group=P name=hoek /><ref group=S name=ferr /> | ||
Revision as of 03:32, 29 December 2024
Experiment measuring the speed of light in moving water This article is about the experiment to measure the relative speed of light in a moving medium. For Fizeau's experiment to measure the absolute speed of light in air, see Fizeau's measurement of the speed of light in air.

The Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Fizeau used a special interferometer arrangement to measure the effect of movement of a medium upon the speed of light.
According to the theories prevailing at the time, light traveling through a moving medium would be dragged along by the medium, so that the measured speed of the light would be a simple sum of its speed through the medium plus the speed of the medium. Fizeau indeed detected a dragging effect, but the magnitude of the effect that he observed was far lower than expected. When he repeated the experiment with air in place of water he observed no effect. His results seemingly supported the partial aether-drag hypothesis of Augustin-Jean Fresnel, a situation that was disconcerting to most physicists. Over half a century passed before a satisfactory explanation of Fizeau's unexpected measurement was developed with the advent of Albert Einstein's theory of special relativity. Einstein later pointed out the importance of the experiment for special relativity, in which it corresponds to the relativistic velocity-addition formula when restricted to small velocities.
Although it is referred to as the Fizeau experiment, Fizeau was an active experimenter who carried out a wide variety of different experiments involving measuring the speed of light in various situations.
Background
Main article: History of electromagnetismAs scientists in the 1700's worked on a theory of light and of electromagnetism, luminiferous aether, a medium that would support waves, was the focus of many experiments. Two critical issues were the relation of aether to motion and its relation to matter. For example, astronomical aberration, the apparent motion of stars observed at different times of year, was proposed to be related to starlight propagated through an aether. In 1846 Fresnel proposed that the portion aether that will move with an object relates to the object's index of refraction of light, which was take to be the ratio of the speed of light in the material to the speed of light in interstellar space. Having recently measured the speed of light in air and water, Fizeau set out to measure the speed of light in moving water.
Experimental setup


A highly simplified representation of Fizeau's 1851 experiment is presented in Fig. 2. Incoming light is split into two beams by a beam splitter (BS) and passed through two columns of water flowing in opposite directions. The two beams are then recombined to form an interference pattern that can be interpreted by an observer.
The simplified arrangement illustrated in Fig. 2 would have required the use of monochromatic light, which would have enabled only dim fringes. Because of white light's short coherence length, use of white light would have required matching up the optical paths to an impractical degree of precision, and the apparatus would have been extremely sensitive to vibration, motion shifts, and temperature effects.
On the other hand, Fizeau's actual apparatus, illustrated in Fig. 3 and Fig. 4, was set up as a common-path interferometer. This guaranteed that the opposite beams would pass through equivalent paths, so that fringes readily formed even when using the sun as a light source.
The double transit of the light was for the purpose of augmenting the distance traversed in the medium in motion, and further to compensate entirely any accidental difference of temperature or pressure between the two tubes, from which might result a displacement of the fringes, which would be mingled with the displacement which the motion alone would have produced; and thus have rendered the observation of it uncertain.
— Fizeau

A light ray emanating from the source S′ is reflected by a beam splitter G and is collimated into a parallel beam by lens L. After passing the slits O1 and O2, two rays of light travel through the tubes A1 and A2, through which water is streaming back and forth as shown by the arrows. The rays reflect off a mirror m at the focus of lens L′, so that one ray always propagates in the same direction as the water stream, and the other ray opposite to the direction of the water stream. After passing back and forth through the tubes, both rays unite at S, where they produce interference fringes that can be visualized through the illustrated eyepiece. The interference pattern can be analyzed to determine the speed of light traveling along each leg of the tube.
Impact
Main article: Aether drag hypothesisAt the time of Fizeau's experiment, two different models of how aether related to moving bodies were discussed, Fresnel's partial drag hypothesis and George Stokes' complete aether drag hypothesis. Fresnel had Augustin-Jean Fresnel (1818) proposed his model to explain an 1810 experiment by Arago. In 1845 Stokes showed that complete aether drag could also explain it. Since Fresnel had no model to explain partial drag, scientists favored Stokes explanation.
According to the Stokes' hypothesis, the speed of light should be increased or decreased when "dragged" along by the water through the aether frame, dependent upon the direction. The overall speed of a beam of light should be a simple additive sum of its speed through the water plus the speed of the water.
That is, if n is the index of refraction of water, so that c/n is the speed of light in stationary water, then the predicted speed of light w in one arm would be
and the predicted speed in the other arm would be
for water with velocity . Hence light traveling against the flow of water should be slower than light traveling with the flow of water. The interference pattern between the two beams when the light is recombined at the observer depends upon the transit times over the two paths.
However Fizeau found that
In other words, light appeared to be dragged by the water, but the magnitude of the dragging was much lower than expected.
The Fizeau experiment forced physicists to accept the empirical validity of an Fresnel's model, that a medium moving through the stationary aether drags light propagating through it with only a fraction of the medium's speed, with a dragging coefficient f related to the index of refraction:
Although Fresnel's hypothesis was empirically successful in explaining Fizeau's results, many experts in the field, including Fizeau himself, found Fresnel's hypothesis partial aether-dragging unsatisfactory. Fresnel had found an empirical formula that worked but no mechanical model of the aether was used to derive it.
Confirmation
Wilhelm Veltmann's colors of light
In 1870 Wilhelm Veltmann demonstrated that Fresnel's formula worked for different frequencies (colors) of light. According the Fresnel's model this would imply different amounts of eather drag for different colors of light. The velocity with white light, a mixture of colors, would be unexplained.
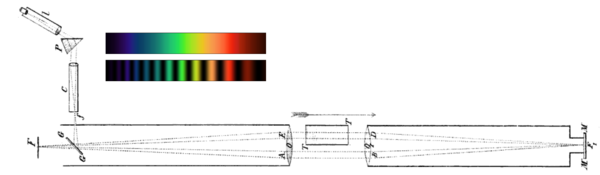
Hoek experiment
See also: Hammar experimentAn indirect confirmation of Fresnel's dragging coefficient was provided by Martin Hoek (1868). His apparatus was similar to Fizeau's, though in his version only one arm contained an area filled with resting water, while the other arm was in the air. As seen by an observer resting in the aether, Earth and hence the water is in motion. So the following travel times of two light rays traveling in opposite directions were calculated by Hoek (neglecting the transverse direction, see image):
The travel times are not the same, which should be indicated by an interference shift. However, if Fresnel's dragging coefficient is applied to the water in the aether frame, the travel time difference (to first order in v/c) vanishes. Upon turning the apparatus table 180 degrees, altering the direction of a hypothetical aether wind, Hoek obtained a null result, confirming Fresnel's dragging coefficient.
In the particular version of the experiment shown here, Hoek used a prism P to disperse light from a slit into a spectrum which passed through a collimator C before entering the apparatus. With the apparatus oriented parallel to the hypothetical aether wind, Hoek expected the light in one circuit to be retarded 7/600 mm with respect to the other. Where this retardation represented an integral number of wavelengths, he expected to see constructive interference; where this retardation represented a half-integral number of wavelengths, he expected to see destructive interference. In the absence of dragging, his expectation was for the observed spectrum to be continuous with the apparatus oriented transversely to the aether wind, and to be banded with the apparatus oriented parallel to the aether wind. His actual experimental results were completely negative.
Mascart's birefringence experiment
Éleuthère Mascart (1872) demonstrated a result for polarized light traveling through a birefringent medium gives different velocities in accordance with Fresnel's empirical formula. However, the result in terms of Fresnel's physical model requires different aether drag in different direction in the medium.
Michelson and Morley confirmation

Albert A. Michelson and Edward W. Morley (1886) repeated Fizeau's experiment with improved accuracy, addressing several concerns with Fizeau's original experiment: (1) Deformation of the optical components in Fizeau's apparatus could cause artifactual fringe displacement; (2) observations were rushed, since the pressurized flow of water lasted only a short time; (3) the laminar flow profile of water flowing through Fizeau's small diameter tubes meant that only their central portions were available, resulting in faint fringes; (4) there were uncertainties in Fizeau's determination of flow rate across the diameter of the tubes. Michelson redesigned Fizeau's apparatus with larger diameter tubes and a large reservoir providing three minutes of steady water flow. His common-path interferometer design provided automatic compensation of path length, so that white light fringes were visible at once as soon as the optical elements were aligned. Topologically, the light path was that of a Sagnac interferometer with an even number of reflections in each light path. This offered extremely stable fringes that were, to first order, completely insensitive to any movement of its optical components. The stability was such that it was possible for him to insert a glass plate at h or even to hold a lighted match in the light path without displacing the center of the fringe system. Using this apparatus, Michelson and Morley were able to completely confirm Fizeau's results not just in water, but also in air.
Zeeman and Lorentz's improved formula
In 1895, Hendrik Lorentz predicted the existence of an extra term due to dispersion:
Since the medium is flowing towards or away from the observer, the light traveling through the medium is Doppler-shifted, and the refractive index used in the formula has to be that appropriate to the Doppler-shifted wavelength. Zeeman verified the existence of Lorentz' dispersion term in 1915. Using a scaled-up version of Michelson's apparatus connected directly to Amsterdam's main water conduit, Zeeman was able to perform extended measurements using monochromatic light ranging from violet (4358 Å) through red (6870 Å) to confirm Lorentz's modified coefficient.
Later confirmations
In 1910, Franz Harress used a rotating device and overall confirmed Fresnel's dragging coefficient. However, he additionally found a "systematic bias" in the data, which later turned out to be the Sagnac effect.
Since then, many experiments have been conducted measuring such dragging coefficients in a diversity of materials of differing refractive index, often in combination with the Sagnac effect. For instance, in experiments using ring lasers together with rotating disks, or in neutron interferometric experiments. Also a transverse dragging effect was observed, i.e. when the medium is moving at right angles to the direction of the incident light.
Lorentz's interpretation
Main articles: Lorentz ether theory and History of Lorentz transformationsIn 1892, Hendrik Lorentz proposed a modification of Fresnel's model, in which the aether is completely stationary. He succeeded in deriving Fresnel's dragging coefficient as the result of an interaction between the moving water with an undragged aether. He also discovered that the transition from one to another reference frame could be simplified by using an auxiliary time variable which he called local time:
In 1895, Lorentz more generally explained Fresnel's coefficient based on the concept of local time. However, Lorentz's theory had the same fundamental problem as Fresnel's: a stationary aether contradicted the Michelson–Morley experiment. So in 1892 Lorentz proposed that moving bodies contract in the direction of motion (FitzGerald-Lorentz contraction hypothesis, since George FitzGerald had already arrived in 1889 at this conclusion). The equations that he used to describe these effects were further developed by him until 1904. These are now called the Lorentz transformations in his honor, and are identical in form to the equations that Einstein was later to derive from first principles. Unlike Einstein's equations, however, Lorentz's transformations were strictly ad hoc, their only justification being that they seemed to work.
Einstein's use of Fizeau's experiment
Main article: Special relativityEinstein showed how Lorentz's equations could be derived as the logical outcome of a set of two simple starting postulates. In addition Einstein recognized that the stationary aether concept has no place in special relativity, and that the Lorentz transformation concerns the nature of space and time. Together with the moving magnet and conductor problem, the negative aether drift experiments, and the aberration of light, the Fizeau experiment was one of the key experimental results that shaped Einstein's thinking about relativity. Robert S. Shankland reported some conversations with Einstein, in which Einstein emphasized the importance of the Fizeau experiment:
He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau's measurements on the speed of light in moving water. "They were enough," he said.
Modern interpretation
Max von Laue (1907) demonstrated that the Fresnel drag coefficient can be explained as a natural consequence of the relativistic formula for addition of velocities. The speed of light in immobile water is c/n. From the velocity composition law it follows that the speed of light observed in the laboratory, where water is flowing with speed v (in the same direction as light) is Thus the difference in speed is (assuming v is small comparing to c, dropping higher order terms) This is accurate when v/c ≪ 1, and agrees with the formula based upon Fizeau's measurements, which satisfied the condition v/c ≪ 1.
See also
References
- Becker, Richard; Sauter, Fritz (1 January 1982). Electromagnetic Fields and Interactions. Courier Corporation. p. 308. ISBN 978-0-486-64290-1. Retrieved 9 March 2023.
- Rohrlich, Fritz (25 August 1989). From Paradox to Reality: Our Basic Concepts of the Physical World. Cambridge University Press. p. 54. ISBN 978-0-521-37605-1. Retrieved 9 March 2023.
- Rosser, W. G. V. (6 January 1992). Introductory Special Relativity. CRC Press. p. 113. ISBN 978-0-85066-838-4. Retrieved 9 March 2023.
- ^ Whittaker, E. T. (1989). A history of the theories of aether & electricity. New York: Dover Publications. ISBN 978-0-486-26126-3.
- Secondary sources
- ^ N David Mermin (2005). It's about time: understanding Einstein's relativity. Princeton University Press. pp. 39ff. ISBN 0-691-12201-6.
- Mascart, Éleuthère Élie Nicolas (1889). Traité d'optique. Paris: Gauthier-Villars. p. 101. Retrieved 9 August 2015.
- ^ Stachel, J. (2005). "Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies". In Kox, A.J.; Eisenstaedt, J (eds.). The universe of general relativity. Boston: Birkhäuser. pp. 1–13. ISBN 0-8176-4380-X. Retrieved 17 April 2012.
- Robert Williams Wood (1905). Physical Optics. The Macmillan Company. p. 514.
- ^ Rafael Ferraro (2007). "Hoek's experiment". Einstein's Space-Time: An Introduction to Special and General Relativity. Springer. pp. 33–35. ISBN 978-0-387-69946-2.
- Cite error: The named reference
Whittakerwas invoked but never defined (see the help page). - Hariharan, P. (2007). Basics of Interferometry, 2nd edition. Elsevier. p. 19. ISBN 978-0-12-373589-8.
- Pauli, Wolfgang (1981) . Theory of Relativity. New York: Dover. ISBN 0-486-64152-X.
- Anderson, R.; Bilger, H.R.; Stedman, G.E. (1994). "Sagnac effect: A century of Earth-rotated interferometers". Am. J. Phys. 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656.
- Stedman, G. E. (1997). "Ring-laser tests of fundamental physics and geophysics". Reports on Progress in Physics. 60 (6): 615–688. Bibcode:1997RPPh...60..615S. doi:10.1088/0034-4885/60/6/001. S2CID 1968825.; see pp. 631–634, and references therein.
- ^ Janssen, Michel; Stachel, John (2010), "The Optics and Electrodynamics of Moving Bodies" (PDF), in John Stachel (ed.), Going Critical, Springer, ISBN 978-1-4020-1308-9
- ^ Miller, A.I. (1981). Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Reading: Addison–Wesley. ISBN 0-201-04679-2.
- Lahaye, Thierry; Labastie, Pierre; Mathevet, Renaud (2012). "Fizeau's "aether-drag" experiment in the undergraduate laboratory". American Journal of Physics. 80 (6): 497. arXiv:1201.0501. Bibcode:2012AmJPh..80..497L. doi:10.1119/1.3690117. S2CID 118401543.
- Norton, John D., John D. (2004), "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905", Archive for History of Exact Sciences, 59 (1): 45–105, Bibcode:2004AHES...59...45N, doi:10.1007/s00407-004-0085-6, S2CID 17459755
- Shankland, R. S. (1963). "Conversations with Albert Einstein". American Journal of Physics. 31 (1): 47–57. Bibcode:1963AmJPh..31...47S. doi:10.1119/1.1969236.
- Primary sources
- ^
Fizeau, H. (1851). "Sur les hypothèses relatives à l'éther lumineux". Comptes Rendus. 33: 349–355.
- English: Fizeau, H. (1851). "The Hypotheses Relating to the Luminous Aether, and an Experiment which Appears to Demonstrate that the Motion of Bodies Alters the Velocity with which Light Propagates itself in their Interior" . Philosophical Magazine. 2: 568–573.
-
Fizeau, H. (1859). "Sur les hypothèses relatives à l'éther lumineux". Ann. Chim. Phys. 57: 385–404.
- English: Fizeau, H. (1860). "On the Effect of the Motion of a Body upon the Velocity with which it is traversed by Light" . Philosophical Magazine. 19: 245–260.
- ^ Hoek, M. (1868). "Determination de la vitesse avec laquelle est entrainée une onde lumineuse traversant un milieu en mouvement" . Verslagen en Mededeelingen. 2: 189–194.
- ^ Michelson, A. A.; Morley, E.W. (1886). "Influence of Motion of the Medium on the Velocity of Light". Am. J. Sci. 31 (185): 377–386. Bibcode:1886AmJS...31..377M. doi:10.2475/ajs.s3-31.185.377. S2CID 131116577.
- ^ Jones, R. V. (1972). "'Fresnel Aether Drag' in a Transversely Moving Medium". Proceedings of the Royal Society A. 328 (1574): 337–352. Bibcode:1972RSPSA.328..337J. doi:10.1098/rspa.1972.0081. S2CID 122749907.
- ^ Zeeman, Pieter (1915). "Fresnel's coefficient for light of different colours. (Second part)". Proc. Kon. Acad. Van Weten. 18: 398–408. Bibcode:1915KNAB...18..398Z.
- Zeeman, Pieter (1914). "Fresnel's coefficient for light of different colours. (First part)". Proc. Kon. Acad. Van Weten. 17: 445–451. Bibcode:1914KNAB...17..445Z.
- Macek, W. M. (1964). "Measurement of Fresnel Drag with the Ring Laser". Journal of Applied Physics. 35 (8): 2556–2557. Bibcode:1964JAP....35.2556M. doi:10.1063/1.1702908.
- Bilger, H. R.; Zavodny, A. T. (1972). "Fresnel Drag in a Ring Laser: Measurement of the Dispersive Term". Physical Review A. 5 (2): 591–599. Bibcode:1972PhRvA...5..591B. doi:10.1103/PhysRevA.5.591.
- Bilger, H. R.; Stowell, W. K. (1977). "Light drag in a ring laser – An improved determination of the drag coefficient". Physical Review A. 16 (1): 313–319. Bibcode:1977PhRvA..16..313B. doi:10.1103/PhysRevA.16.313.
- Sanders, G. A.; Ezekiel, Shaoul (1988). "Measurement of Fresnel drag in moving media using a ring-resonator technique". Journal of the Optical Society of America B. 5 (3): 674–678. Bibcode:1988JOSAB...5..674S. doi:10.1364/JOSAB.5.000674. S2CID 14298827.
- Klein, A. G.; Opat, G. I.; Cimmino, A.; Zeilinger, A.; Treimer, W.; Gähler, R. (1981). "Neutron Propagation in Moving Matter: The Fizeau Experiment with Massive Particles". Physical Review Letters. 46 (24): 1551–1554. Bibcode:1981PhRvL..46.1551K. doi:10.1103/PhysRevLett.46.1551.
- Bonse, U.; Rumpf, A. (1986). "Interferometric measurement of neutron Fizeau effect". Physical Review Letters. 56 (23): 2441–2444. Bibcode:1986PhRvL..56.2441B. doi:10.1103/PhysRevLett.56.2441. PMID 10032993.
- Arif, M.; Kaiser, H.; Clothier, R.; Werner, S. A.; Hamilton, W. A.; Cimmino, A.; Klein, A. G. (1989). "Observation of a motion-induced phase shift of neutron de Broglie waves passing through matter near a nuclear resonance". Physical Review A. 39 (3): 931–937. Bibcode:1989PhRvA..39..931A. doi:10.1103/PhysRevA.39.931. PMID 9901325.
- Jones, R. V. (1975). ""Aether Drag" in a Transversely Moving Medium". Proceedings of the Royal Society A. 345 (1642): 351–364. Bibcode:1975RSPSA.345..351J. doi:10.1098/rspa.1975.0141. S2CID 122055338.
- Laue, Max von (1907), "Die Mitführung des Lichtes durch bewegte Körper nach dem Relativitätsprinzip" [The Entrainment of Light by Moving Bodies in Accordance with the Principle of Relativity], Annalen der Physik, 328 (10): 989–990, Bibcode:1907AnP...328..989L, doi:10.1002/andp.19073281015
| Tests of special relativity | |
|---|---|
| Speed/isotropy | |
| Lorentz invariance | |
| Time dilation Length contraction | |
| Relativistic energy | |
| Fizeau/Sagnac | |
| Alternatives | |
| General | |


 .
Hence light traveling against the flow of water should be slower than light traveling with the flow of water.
The
.
Hence light traveling against the flow of water should be slower than light traveling with the flow of water.
The 





 Thus the difference in speed is (assuming v is small comparing to c, dropping higher order terms)
Thus the difference in speed is (assuming v is small comparing to c, dropping higher order terms)

 This is accurate when v/c ≪ 1, and agrees with the formula based upon Fizeau's measurements, which satisfied the condition v/c ≪ 1.
This is accurate when v/c ≪ 1, and agrees with the formula based upon Fizeau's measurements, which satisfied the condition v/c ≪ 1.