| Revision as of 16:04, 7 December 2004 editKusma (talk | contribs)Autopatrolled, Administrators59,838 edits remove "helical edges" (not true)← Previous edit | Revision as of 16:14, 7 December 2004 edit undoKusma (talk | contribs)Autopatrolled, Administrators59,838 edits removed link to misleading soap film pageNext edit → | ||
| Line 5: | Line 5: | ||
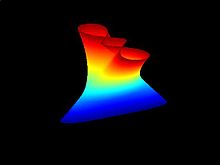
| In ], a '''minimal surface''' is a surface with mean ] of zero. | In ], a '''minimal surface''' is a surface with mean ] of zero. | ||
| This includes, but is not limited to, surfaces of minimum area subject to constraints on the location of their boundary. | This includes, but is not limited to, surfaces of minimum area subject to constraints on the location of their boundary. | ||
| The area-minimizing surfaces can be physically realized as |
The area-minimizing surfaces can be physically realized as soap films. Examples of minimal surfaces include ]s and ]s. | ||
| Minimal surfaces have become an area of intense mathematical and scientific study over the past 15 years, specifically in the areas of ] and ], due to their anticipated ] applications. | Minimal surfaces have become an area of intense mathematical and scientific study over the past 15 years, specifically in the areas of ] and ], due to their anticipated ] applications. | ||
Revision as of 16:14, 7 December 2004
In mathematics, a minimal surface is a surface with mean curvature of zero. This includes, but is not limited to, surfaces of minimum area subject to constraints on the location of their boundary. The area-minimizing surfaces can be physically realized as soap films. Examples of minimal surfaces include catenoids and helicoids.
Minimal surfaces have become an area of intense mathematical and scientific study over the past 15 years, specifically in the areas of molecular engineering and materials science, due to their anticipated nanotechnology applications.
See also
soap bubble, Plateau's problem
External links
Touching Soap Films graphical introduction to minimal surfaces and soap films.
Categories: