Misplaced Pages

Revision as of 09:53, 10 March 2013

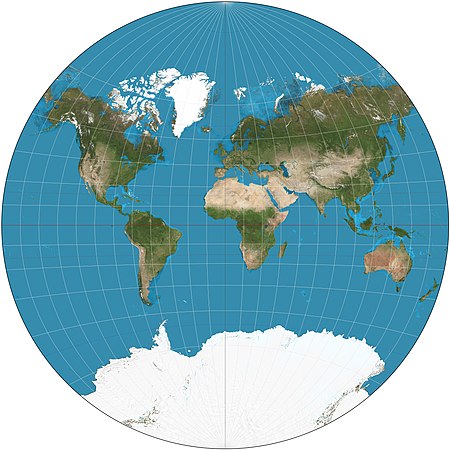
The van der Grinten projection is a compromise map projection that is neither equal-area nor conformal. It projects the entire Earth into a circle, though the polar regions are subject to extreme distortion. The projection was the first of four proposed by Alphons J. van der Grinten in 1904, and, unlike most projections, is an arbitrary geometric construction on the plane. It was made famous when the National Geographic Society adopted it as their reference map of the world from 1922 until 1988.

The geometric construction given by van der Grinten can be written algebraically:

${\displaystyle x={\frac {\pm \pi \left(A\left(G-P^{2}\right)+{\sqrt {A^{2}\left(G-P^{2}\right)^{2}-\left(P^{2}+A^{2}\right)\left(G^{2}-P^{2}\right)}}\right)}{P^{2}+A^{2}}}\,}$

${\displaystyle y={\frac {\pm \pi \left(PQ-A{\sqrt {\left(A^{2}+1\right)\left(P^{2}+A^{2}\right)-Q^{2}}}\right)}{P^{2}+A^{2}}}}$

where ${\displaystyle x\,}$ takes the sign of ${\displaystyle \lambda -\lambda _{0}\,}$, ${\displaystyle y\,}$ takes the sign of ${\displaystyle \phi \,}$ and

${\displaystyle A={\frac {1}{2}}|{\frac {\pi }{\lambda -\lambda _{0}}}-{\frac {\lambda -\lambda _{0}}{\pi }}|}$

${\displaystyle G={\frac {\cos \theta }{\sin \theta +\cos \theta -1}}}$

${\displaystyle P=G\left({\frac {2}{\sin \theta }}-1\right)}$

${\displaystyle \theta =\arcsin |{\frac {2\phi }{\pi }}|}$

${\displaystyle Q=A^{2}+G\,}$

Should it occur that ${\displaystyle \phi =0\,}$, then

${\displaystyle x=\left(\lambda -\lambda _{0}\right)\,}$

${\displaystyle y=0\,}$

Similarly, if ${\displaystyle \lambda =\lambda _{0}\,}$ or ${\displaystyle \phi =\pm \pi /2\,}$, then

${\displaystyle x=0\,}$

${\displaystyle y=\pm \pi \tan {\theta /2}}$

In all cases, ${\displaystyle \phi \,}$ is the latitude, ${\displaystyle \lambda \,}$ is the longitude, and ${\displaystyle \lambda _{0}\,}$ is the central meridian of the projection.

Notes

1. Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp.258-262, ISBN 0-226-76747-7.
2. Map Projections - A Working Manual, USGS Professional Paper 1395, John P. Snyder, 1987, pp.239-242

References

• "Projections by Van der Grinten, and variations".

This cartography or mapping term article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Cartographic projections
• Cartography stubs