Misplaced Pages

This is an old revision of this page, as edited by Tosha (talk | contribs) at 04:49, 21 March 2004. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation between the three sides of a right triangle. The theorem is named after and commonly attributed to the 6th century BC Greek philosopher and mathematician Pythagoras, although the facts of the theorem were known before he lived.

The theorem

The Pythagorean theorem states:

The sum of the the squares on the legs of a right triangle is equal to the square on the hypotenuse.

A right triangle is a triangle with one right angle; the legs are the two sides that make up the right angle, and the hypotenuse is the third side opposite the right angle. In the picture below, a and b are the legs of a right triangle, and c is the hypotenuse:

File:Pythagorean.png

Pythagoras perceived the theorem in this geometric fashion, as a statement about areas of squares:

The area of the purple square is equal to the sum of the areas of the blue and red squares.

Using algebra, one can reformulate the theorem into its modern expression by noting that the area of a square (an equal-sided rectangle) is the square (second power) of the length of its side:

Given a right triangle with legs of lengths a and b and hypotenuse of length c, then

${\displaystyle a^{2}+b^{2}=c^{2}}$

A visual proof

Perhaps this theorem has a greater variety of different known proofs than any other. (The law of quadratic reciprocity may also be a contender for that distinction).

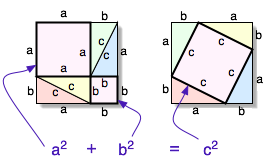
This illustration depicts one of them. In the right half of the picture, four copies of this triangle surround a large square. The pink diagonal square in the center is the square on the hypotenuse. Move the four triangles within the large square so that they are arranged as in the left half of the picture. Then the pink area not included within the four triangles makes up the squares on the legs. Consequently the sum of the areas of the squares on the legs equals the area of the square on the hypotenuse. Q.E.D.

NB: This proof is often considered very simple, but it has a hidden gap. The properties of area used here are not as elementary as one might think; in fact, proving the necessary properies is harder than the Pythagorean theorem itself. That is the reason why this proof is not used in good introductions to Euclidean geometry.

There are many different proofs of the Pythagorean theorem; United States President James Garfield developed one himself. One of the proofs is based on Euler's formula in complex analysis. (See also the external links below for a sampling of the many different proofs of the Pythagorean theorem.)

The converse

The converse of the Pythagorean theorem is also true:

For any three positive numbers a, b, and c such that a + b = c, there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.

This can be proven using the law of cosines which is a generalization of the Pythagorean theorem applying to all (Euclidean) triangles, not just right-angled ones.

Variations/generalisations

• The Pythagorean theorem was generalised by Euclid in his Elements:

If one erects similar figures (see Euclidean geometry) on the sides of a right triangle, then the sum of the areas of the two smaller ones equals the area of the larger one.

• The Pythagorean theorem stated in Cartesian coordinates is the formula for the distance between points in the plane -- if (x₀, y₀) and (x₁, y₁) are points in the plane, then the distance between them is given by

${\displaystyle {\sqrt {(x_{1}-x_{0})^{2}+(y_{1}-y_{0})^{2}}}.}$

This distance formula generalises to inner product spaces, and the version of the Pythagorean theorem in inner product spaces is known as Parseval's identity.

• Given two vectors v and w in a normed vector space, the Pythagorean theorem takes the following form:

||v + w|| = ||v|| + ||w|| if and only if v and w are orthogonal.

• The Pythagorean theorem also generalizes to higher-dimensional simplexes. If a tetrahedron has a right angle corner (a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This is called de Gua's theorem.

• For the right triangle on unit sphere the Pythagorean theorem takes form

${\displaystyle \cos c=\cos a\cos b}$

For the hyperbolic plane (with Gauss curvature −1).

${\displaystyle \cosh c=\cosh a\cosh b}$

where cosh is the hyperbolic cosine.

See also

• Pythagorean triple
• Orthogonality
• Linear algebra
• Synthetic geometry
• Fermat's last theorem
• Parallelogram law

External links

• Several proofs of the Pythagorean theorem
• Using the Pythagorean theorem and a Microsoft Windows calculator to calculate the sides of an octagon