Misplaced Pages

This is an old revision of this page, as edited by 190.188.9.30 (talk) at 21:27, 24 December 2009 (→Software support). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

HSL and HSV are two related representations of points in an RGB color model that attempt to describe perceptual color relationships more accurately than RGB, while remaining computationally simple. HSL stands for hue, saturation and lightness, while HSV stands for hue, saturation and value.

HSI and HSB are alternative names for these concepts, often substituting intensity and brightness for lightness and/or value; their definitions are less standardized, but they are typically interpreted to be synonymous with HSL and HSV.

Both HSL and HSV can be thought of as describing colors as points in a cylinder (called a color solid) whose central axis ranges from black at the bottom to white at the top, with neutral colors between them. The angle around the axis corresponds to “hue”, the distance from the axis corresponds to “saturation”, and the distance along the axis corresponds to “lightness”, “value” or “brightness”.

The two representations are similar in purpose, but differ somewhat in approach. Both are mathematically cylindrical, but while HSV (hue, saturation, value) can be thought of conceptually as an inverted cone of colors (with a black point at the bottom, and fully-saturated colors around a circle at the top), HSL conceptually represents a double-cone or sphere (with white at the top, black at the bottom, and the fully-saturated colors around the edge of a horizontal cross-section with middle gray at its center). Note that while “hue” in HSL and HSV refers to the same attribute, their definitions of “saturation” differ dramatically.

Because HSL and HSV are simple transformations of device-dependent RGB models, the physical colors defined by (h, s, l) or (h, s, v) triplets depend on the colors of the red, green, and blue primaries of the device or of the particular RGB space, and on the gamma compression used to represent the amounts of those primaries. Each unique RGB device therefore has unique HSL and HSV spaces to accompany it, and an (h, s, l) or (h, s, v) triplet can therefore become definite when it is tied to a particular RGB color space (such as sRGB).

Both models were first formally described in 1978 by Alvy Ray Smith, though the concept of describing colors in three dimensions dates to the 18th century (see section below).

Usage

This section called "Usage" does not cite any sources. Please help improve this section called "Usage" by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "HSL and HSV" – news · newspapers · books · scholar · JSTOR (August 2009) (Learn how and when to remove this message)

It is sometimes preferable in working with art materials, digitized images, or other media, to use the HSV or HSL color model over alternative models such as RGB or CMYK, because of differences in the ways the models emulate how humans perceive color. RGB and CMYK are additive and subtractive models, respectively, modelling the way that primary color lights or pigments (respectively) combine to form new colors when mixed.

The HSV model is commonly used in computer graphics applications. In various application contexts, a user must choose a color to be applied to a particular graphical element. When used in this way, the HSV color wheel is often used. In it, the hue is represented by a circular region; a separate triangular region may be used to represent saturation and value. Typically, the vertical axis of the triangle indicates saturation, while the horizontal axis corresponds to value. In this way, a color can be chosen by first picking the hue from the circular region, then selecting the desired saturation and value from the triangular region.

Another visualization method of the HSV model is the cone. In this representation, the hue is depicted as a three-dimensional conical formation of the color wheel. The saturation is represented by the distance from the center of a circular cross-section of the cone, and the value is the distance from the pointed end of the cone. Some representations use a hexagonal cone, or hexcone, instead of a circular cone. This method is well-suited to visualizing the entire HSV color space in a single object; however, due to its three-dimensional nature, it is not well-suited to color selection in two-dimensional computer interfaces.

The HSV color space could also be visualized as a cylindrical object; similar to the cone above, the hue varies along the outer circumference of a cylinder, with saturation again varying with distance from the center of a circular cross-section. Value again varies from top to bottom. Such a representation might be considered the most mathematically accurate model of the HSV color space; however, in practice the number of visually distinct saturation levels and hues decreases as the value approaches black. Additionally, computers typically store RGB values with a limited range of precision; the constraints of precision, coupled with the limitations of human color perception, make the cone visualization more practical in most cases.

Comparison of HSL and HSV

HSL is similar to HSV. For some people, HSL better reflects the intuitive notion of "saturation" and "lightness" as two independent parameters, but for others its definition of saturation is wrong, as for example a very pastel, almost white color can be defined as fully saturated in HSL.

The CSS3 specification from the W3C states, "Advantages of HSL are that it is symmetrical to lightness and darkness (which is not the case with HSV for example)…" This means that:

• In HSL, the Saturation component always goes from fully saturated color to the equivalent gray (in HSV, with V at maximum, it goes from saturated color to white, which may be considered counterintuitive).
• The Lightness in HSL always spans the entire range from black through the chosen hue to white (in HSV, the V component only goes half that way, from black to the chosen hue).

Comparison with other color models

This section needs expansion. You can help by adding to it. (May 2008)

The HSV tristimulus space does not technically support a one-to-one mapping to physical power spectra as measured in radiometry. Thus it is not generally advisable to try to make direct comparisons between HSV coordinates and physical light properties such as wavelength or amplitude.

Comparison with color science

The terms attributed to the "L" and "V" components of the HSL and HSV color models may be misleading since they have little to do with color science definitions of the terms. In photometry, concepts such as lightness and luminance relate to a weighted spectrum, in which green is much more luminous than blue, and red is between; but in HSL and HSV, the "L" and "V" dimensions treat the three color channels equally.

• Lightness or value refers to the perceived reflectance of a surface, or to relative luminous reflectance of a colored surface patch.

• Luminance typically refers to relative luminance, which is based on the photometric definition of luminance but normalized with respect to a reference white.

• Luminosity typically (and incorrectly) refers to relative luminance. This usage was popularized by Adobe Photoshop; in the documentation of the CS3 version, the luminosity blending mode is still present, but is described in terms of luminance: "Luminosity: Creates a result color with the hue and saturation of the base color and the luminance of the blend color."

Spherical and other 3D mappings

HSL and HSV are related to older, three-dimensional color-order systems such as Philipp Otto Runge's color sphere (Farbenkugel) and the Munsell color system, both of which are structured around a neutral black-to-white axis, with lightness extending along the polar axis, hue represented by longitude, and saturation a fraction of the radius of the disk at a constant lightness or latitude. Munsell refers to the colorfulness dimension as chroma rather than saturation, but uses hue and lightness in the same way as HSL. Modern works also sometimes use this spherical model.

Since the entire top and bottom surfaces of the HSL cylinder are white and black, respectively, no information is lost when collapsing them to points at the sphere's poles. The same is true for the HSL bi-cone, another popular way to shrink the white and black surfaces to points. The bi-cone fits the same description as the sphere given above, but with a different profile of radius versus lightness. For HSV, on the other hand, the top surface of the cylinder is not white, so only the bottom surface can be collapsed to a point, resulting in the popular mapping to a cone.

Formal specifications

Template:Fixbunching Template:Fixbunching

HSL and HSV are defined mathematically by transformations between the r, g, and b color coordinates in the RGB model and the h, s, l, and v coordinates in the HSL and HSV models.

Conversion from RGB to HSL overview

The logic of the conversion is as follows:

Lightness: In RGB, the closer we are to the MAX RGB value for each r, g , b the closer we are getting to white, and thus the closer we are getting to full brightness. So lightness is dependent on how close our average RGB values are to white.

Saturation: There are two factors that determine the "strength" of the saturation. The first is the distances between the different RGB values. The closer they are together, the more the RGB values neutralize each other, and the less the hue is emphasized, thus lowering the saturation. (R = G = B means no saturation at all.) The second factor is the distance the RGB values are from the midpoint. This is because the closer they are to 0, the darker they are until they are totally black (and thus no saturation); and, the closer they get to MAX value, the brighter they are until totally white (and once again no saturation).

Hue: The logic here is to map the RGB values to different hues on a circle circumference.

Conversion from RGB to HSL or HSV

Let r, g, b ∈ be the red, green, and blue coordinates, respectively, of a color in RGB space.

Let max be the greatest of r, g, and b, and min the least.

To find the hue angle h ∈ for either HSL or HSV space, compute:

${\displaystyle h={\begin{cases}0,&{\mbox{if }}\max =\min \\(60^{\circ }\times {\frac {g-b}{\max -\min }}+360^{\circ })\;{\bmod {\;}}360^{\circ },&{\mbox{if }}\max =r\\60^{\circ }\times {\frac {b-r}{\max -\min }}+120^{\circ },&{\mbox{if }}\max =g\\60^{\circ }\times {\frac {r-g}{\max -\min }}+240^{\circ },&{\mbox{if }}\max =b\end{cases}}}$

To find saturation and lightness s, l ∈ for HSL space, compute:

${\displaystyle l={\tfrac {1}{2}}(\max +\min )}$

${\displaystyle s={\begin{cases}0,&{\mbox{if }}\max =\min \\{\frac {\max -\min }{\max +\min }}={\frac {\max -\min }{2l}},&{\mbox{if }}l\leq {\frac {1}{2}}\\{\frac {\max -\min }{2-(\max +\min )}}={\frac {\max -\min }{2-2l}},&{\mbox{if }}l>{\frac {1}{2}}\end{cases}}}$

The value of h is generally normalized to lie between 0 and 360°, and h = 0 is used when max = min (that is, for grays) though the hue has no geometric meaning there, where the saturation s = 0. Similarly, the choice of 0 as the value for s when l is equal to 0 or 1 is arbitrary.

HSL and HSV have the same definition of hue, but the other components differ. The values for s and v of an HSV color are defined as follows:

${\displaystyle s={\begin{cases}0,&{\mbox{if }}\max =0\\{\frac {\max -\min }{\max }}=1-{\frac {\min }{\max }},&{\mbox{otherwise}}\end{cases}}}$

${\displaystyle v=\max \,}$

The range of HSV and HSL vectors is a cube in the cartesian coordinate system; but since hue is really a cyclic property, it is not so necessary or appropriate to unwrap it, with a cut at 0 (red), into a linear coordinate. Therefore, visualizations of these spaces usually involve hue circles; cylindrical and conical (bi-conical for HSL) depictions are most popular; spherical depictions and other color solids are also possible.

Conversion from HSL to RGB

Given a color defined by (h, s, l) values in HSL space, with h in the semi-open interval , representing the saturation and lightness, respectively, a corresponding (r, g, b) triplet in RGB space, with r, g, and b also in range , and corresponding to red, green, and blue, respectively, can be computed as follows:

First, if s = 0, then the resulting color is achromatic, or gray. In this special case, r, g, and b all equal l. Note that the value of h is ignored, and may be undefined in this situation.

The following procedure can be used, even when s is zero:

${\displaystyle q={\begin{cases}l\times (1+s),&{\mbox{if }}l<{\frac {1}{2}}\\l+s-(l\times s),&{\mbox{if }}l\geq {\frac {1}{2}}\end{cases}}}$

${\displaystyle p=2\times l-q\,}$

${\displaystyle h_{k}={h \over 360}\,}$ (h normalized to be in the range )

${\displaystyle t_{R}=h_{k}+{\frac {1}{3}}\,}$

${\displaystyle t_{G}=h_{k}\,}$

${\displaystyle t_{B}=h_{k}-{\frac {1}{3}}\,}$

${\displaystyle {\mbox{if }}t_{C}<0\rightarrow t_{C}=t_{C}+1.0\quad {\mbox{for each}}\,C\in \{R,G,B\}}$

${\displaystyle {\mbox{if }}t_{C}>1\rightarrow t_{C}=t_{C}-1.0\quad {\mbox{for each}}\,C\in \{R,G,B\}}$

The above operation is a modulo, so it can be simply expressed as :

${\displaystyle t_{c}=t_{c}\mod 1}$

Compute each color component Color_C of the vector (Color_R, Color_G, Color_B) = (r, g, b),

${\displaystyle {Color}_{C}={\begin{cases}p+\left((q-p)\times 6\times t_{C}\right),&{\mbox{if }}t_{C}<{\frac {1}{6}}\\q,&{\mbox{if }}{\frac {1}{6}}\leq t_{C}<{\frac {1}{2}}\\p+\left((q-p)\times 6\times ({\frac {2}{3}}-t_{C})\right),&{\mbox{if }}{\frac {1}{2}}\leq t_{C}<{\frac {2}{3}}\\p,&{\mbox{otherwise }}\end{cases}}}$

${\displaystyle {\mbox{for each}}\,C\in \{R,G,B\}}$

Conversion from HSV to RGB

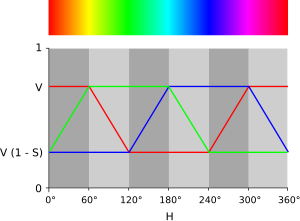
Similarly, given a color defined by (h, s, v) values in HSV space, with h as above, and with s and v varying between 0 and 1, representing the saturation and value, respectively, a corresponding (r, g, b) triplet in RGB space can be computed:

${\displaystyle h_{i}=\left\lfloor {\frac {h}{60}}\right\rfloor \mod 6}$

${\displaystyle f={\frac {h}{60}}-\left\lfloor {\frac {h}{60}}\right\rfloor }$

${\displaystyle p=v\times (1-s)\,}$

${\displaystyle q=v\times (1-f\times s)\,}$

${\displaystyle t=v\times (1-(1-f)\times s)\,}$

Compute color vector (r, g, b),

${\displaystyle (r,g,b)={\begin{cases}(v,t,p),&{\mbox{if }}h_{i}=0\\(q,v,p),&{\mbox{if }}h_{i}=1\\(p,v,t),&{\mbox{if }}h_{i}=2\\(p,q,v),&{\mbox{if }}h_{i}=3\\(t,p,v),&{\mbox{if }}h_{i}=4\\(v,p,q),&{\mbox{if }}h_{i}=5\\\end{cases}}}$

Examples

The R, G, B, S and L values shown below are in the range of 0.0 to 1.0. The H values are in the range of 0° to 360°.

Software support

In software, a hue-based color model (HSV or HSL) is usually presented to the user in the form of a linear or circular hue chooser and a two-dimensional area (usually a square or a triangle) where the user can choose saturation and value/lightness for the selected hue. With this representation, the difference between HSV and HSL is irrelevant. However, many programs also let the user select a color via linear sliders or numeric entry fields, and for those controls, usually either HSL or HSV (not both) are used. HSV is traditionally more common. Here are some examples:

Applications that support HSV for color selection:

• Apple Mac OS and Mac OS X system color picker (one view uses a color wheel for H/S and a slider for V, another view uses three sliders)
• Xara Xtreme
• Blender
• Microsoft Windows Aero color picker (uses three sliders: Hue, Saturation, and Brightness.)
• PB MapInfo Pro

Applications that support HSL for color selection:

• The W3C CSS3 specification
• Macromedia Studio
• Microsoft Windows system color picker (including Microsoft Paint)
• Paint Shop Pro

Applications that support both HSV and HSL for color selection:

• Bryce
• ImageMagick (refers to HSV as 'HSB')
• Inkscape (HSV color selection is on the 'Wheel' tab)
• Pixel image editor (starting from Beta5)
• Pixia
• Chasys Draw IES
• Paint tool SAI

Applications that support HSV for color selection and HSL for image color adjustment:

• The GIMP
• Paint.NET
• Adobe graphic applications (Illustrator, Photoshop, and others)

See also

• Color theory
• Color wheel
• TSL color space

References

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "HSL and HSV" – news · newspapers · books · scholar · JSTOR (June 2007) (Learn how and when to remove this message)

1. Gonzalez, Rafael C. (2007). Digital Image Processing. Prentice Hall. pp. 407–413. ISBN 013168728X, 9780131687288. {{cite book}}: Check |isbn= value: invalid character (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
2. "The HSB/HLS Color Model - Color Models - Technical Guides". Adobe. Retrieved 2009-06-29.
3. Jewett, Tom (1997–2009). "Colors: HSB". Retrieved 2009-06-29.{{cite web}}: CS1 maint: date format (link)
4. Willmore, Ben (2005). Adobe Photoshop CS2: studio techniques. Adobe Press. p. 280. ISBN 0321321898, 9780321321893. {{cite book}}: Check |isbn= value: invalid character (help)
5. Alvy Ray Smith (August 1978). "Color Gamut Transform Pairs". Computer Graphics. 12 (3): 12. doi:10.1145/965139.807361. {{cite journal}}: Unknown parameter |curly= ignored (help)
6. Kuehni, Rolf G. (February 2002). "The early development of the Munsell system". Color Research and Application. 27 (1): 20–27. doi:10.1002/col.10002. {{cite journal}}: Unknown parameter |curly= ignored (help)CS1 maint: date and year (link).
7. Edward H. Adelson (2000). "Lightness Perception and Lightness Illusions – Some terminology". Massachusetts Institute of Technology. Retrieved 2007-07-17. {{cite web}}: Unknown parameter |curly= ignored (help)
8. "List of Blending Modes". Adobe Help Resource Center. Retrieved 2007-11-10. {{cite web}}: Unknown parameter |curly= ignored (help)
9. Phil Nelson (2007). The Photographer's Guide to Color Management: Professional Techniques for Consistent Results. Amherst Media, Inc. ISBN 1584282045.
10. Abhay Sharma (2003). Understanding Color Management. Thomson Delmar Learning. ISBN 1401814476.
11. John C. Russ (2005). Image Analysis Of Food Microstructure. CRC Press. ISBN 0849322413.
12. Richard Prikryl (2004). Dimension Stone 2004 - New Perspectives for a Traditional Building Material. Taylor & Francis. ISBN 9058096750.
13. Max K. Agoston (2005). Computer Graphics and Geometric Modeling: Implementation and Algorithms. Springer. ISBN 1852338180.
14. John C. Russ (2005). Image Analysis Of Food Microstructure. CRC Press. ISBN 0849322413.

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (June 2009) (Learn how and when to remove this message)

• Raphael Gonzalez, Richard E. Woods (2002) Digital Image Processing, 2nd ed. Prentice Hall Press, ISBN 0-201-18075-8, p. 295.
• Charles Poynton. “What are HSB and HLS?” Color FAQ. 28 November 2006.
• Donald Hearn, M. Pauline Baker (1986) Computer Graphics. Prentice Hall International, ISBN 0-13-165598-1, pp. 302–205.

External links

• An explanation of HSL and how it differs from RGB can be found in the W3C's CSS3 Color Module.
• Formulas for converting to and from RGB can be found on EasyRGB.com.
• Demonstrative color conversion applet
• HSV Colors by Hector Zenil, The Wolfram Demonstrations Project.
• HSL at CSS3 . Info very good and simple explanation of HSL
• An algorithm and code for performing HSV transformations directly on RGB colors
• jQuery Color Picker - jQCP

v t e Color space
List of color spaces Color models
CAM	CIECAM02 iCAM CAM16 CIECAM16
CIE	XYZ (1931) RGB (1931) YUV (1960) UVW (1964) CIELAB (1976) CIELUV (1976) CIECAM02 CIECAM16
RGB	RGB color spaces sRGB rg chromaticity Adobe Wide-gamut ProPhoto scRGB DCI-P3 Rec. 601 SMPTE 240M/"C" Rec. 709 Rec. 2020 Rec. 2100
Y′UV	YUV PAL YDbDr SECAM YIQ NTSC YCbCr Rec. 601 Rec. 709 Rec. 2020 Rec. 2100 ICtCp Rec. 2100 YPbPr MAC xvYCC YCoCg
Other	CcMmYK CMYK ColorADD Coloroid LMS Hexachrome HSL, HSV HCL Imaginary color Oklab OSA-UCS PCCS RG RYB HWB YJK TSL
Color systems and standards	ACES ANPA Colour Index International CI list of dyes DIC Federal Standard 595 HKS ICC profile ISCC–NBS Munsell NCS Ostwald Pantone RAL list JIS Z8102 [ja]
For the vision capacities of organisms or machines, see  Color vision.

• Color space