 The series 1 + 1 + 1 + 1 + ⋯
The series 1 + 1 + 1 + 1 + ⋯ After smoothing
After smoothing
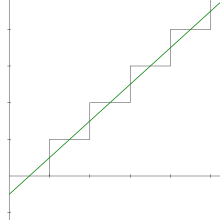
In mathematics, 1 + 1 + 1 + 1 + ⋯, also written , , or simply , is a divergent series. Nevertheless, it is sometimes imputed to have a value of , especially in physics. This value can be justified by certain mathematical methods for obtaining values from divergent series, including zeta function regularization.
As a divergent series
1 + 1 + 1 + 1 + ⋯ is a divergent series, meaning that its sequence of partial sums does not converge to a limit in the real numbers.
The sequence 1 can be thought of as a geometric series with the common ratio 1. For some other divergent geometric series, including Grandi's series with ratio −1, and the series 1 + 2 + 4 + 8 + ⋯ with ratio 2, one can use the general solution for the sum of a geometric series with base 1 and ratio , obtaining , but this summation method fails for 1 + 1 + 1 + 1 + ⋯, producing a division by zero.
Together with Grandi's series, this is one of two geometric series with rational ratio that diverges both for the real numbers and for all systems of p-adic numbers.
In the context of the extended real number line
since its sequence of partial sums increases monotonically without bound.
Zeta function regularization
Where the sum of n occurs in physical applications, it may sometimes be interpreted by zeta function regularization, as the value at s = 0 of the Riemann zeta function:
The two formulas given above are not valid at zero however, but the analytic continuation is
Using this one gets (given that Γ(1) = 1),
where the power series expansion for ζ(s) about s = 1 follows because ζ(s) has a simple pole of residue one there. In this sense 1 + 1 + 1 + 1 + ⋯ = ζ(0) = −1/2.
Emilio Elizalde presents a comment from others about the series, suggesting the centrality of the zeta function regularization of this series in physics:
In a short period of less than a year, two distinguished physicists, A. Slavnov and F. Yndurain, gave seminars in Barcelona, about different subjects. It was remarkable that, in both presentations, at some point the speaker addressed the audience with these words: 'As everybody knows, 1 + 1 + 1 + ⋯ = −1/2.' Implying maybe: If you do not know this, it is no use to continue listening.
See also
- Grandi's series
- 1 − 2 + 3 − 4 + · · ·
- 1 + 2 + 3 + 4 + · · ·
- 1 + 2 + 4 + 8 + · · ·
- 1 − 2 + 4 − 8 + ⋯
- 1 − 1 + 2 − 6 + 24 − 120 + · · ·
- Harmonic series
Notes
- Tao, Terence (April 10, 2010), The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation, retrieved January 30, 2014
- Emphasis in original. Elizalde, Emilio (2004). "Cosmology: Techniques and Applications". Proceedings of the II International Conference on Fundamental Interactions. arXiv:gr-qc/0409076. Bibcode:2004gr.qc.....9076E.
External links
| Sequences and series | ||||||
|---|---|---|---|---|---|---|
| Integer sequences |
|  | ||||
| Properties of sequences | ||||||
| Properties of series |
| |||||
| Explicit series | ||||||
| Kinds of series | ||||||
| Hypergeometric series | ||||||
 ,
,  , or simply
, or simply  , is a
, is a  , especially in physics. This value can be justified by certain mathematical methods for obtaining values from divergent series, including
, especially in physics. This value can be justified by certain mathematical methods for obtaining values from divergent series, including  , obtaining
, obtaining  , but this summation method fails for 1 + 1 + 1 + 1 + ⋯, producing a
, but this summation method fails for 1 + 1 + 1 + 1 + ⋯, producing a 


