 24-cell |
 Truncated 24-cell |
 Bitruncated 24-cell | |
| Schlegel diagrams centered on one (cells at opposite at ) | |||
In geometry, a truncated 24-cell is a uniform 4-polytope (4-dimensional uniform polytope) formed as the truncation of the regular 24-cell.
There are two degrees of truncations, including a bitruncation.
Truncated 24-cell
 Schlegel diagram | ||
|---|---|---|
| Truncated 24-cell | ||
| Type | Uniform 4-polytope | |
| Schläfli symbols | t{3,4,3} tr{3,3,4}= t{3} = | |
| Coxeter diagram | ||
| Cells | 48 | 24 4.6.6 24 4.4.4 |
| Faces | 240 | 144 {4} 96 {6} |
| Edges | 384 | |
| Vertices | 192 | |
| Vertex figure | equilateral triangular pyramid | |
| Symmetry group | F4 , order 1152 | |
| Rotation subgroup | , order 576 | |
| Commutator subgroup | , order 288 | |
| Properties | convex | |
| Uniform index | 23 24 25 | |
The truncated 24-cell or truncated icositetrachoron is a uniform 4-dimensional polytope (or uniform 4-polytope), which is bounded by 48 cells: 24 cubes, and 24 truncated octahedra. Each vertex joins three truncated octahedra and one cube, in an equilateral triangular pyramid vertex figure.
Construction
The truncated 24-cell can be constructed from polytopes with three symmetry groups:
- F4 : A truncation of the 24-cell.
- B4 : A cantitruncation of the 16-cell, with two families of truncated octahedral cells.
- D4 : An omnitruncation of the demitesseract, with three families of truncated octahedral cells.
| Coxeter group | = | = | = |
|---|---|---|---|
| Schläfli symbol | t{3,4,3} | tr{3,3,4} | t{3} |
| Order | 1152 | 384 | 192 |
| Full symmetry group |
<> = ] = | ||
| Coxeter diagram | |||
| Facets | 3: 1: |
2: 1: 1: |
1,1,1: 1: |
| Vertex figure | 
|
|

|
Zonotope
It is also a zonotope: it can be formed as the Minkowski sum of the six line segments connecting opposite pairs among the twelve permutations of the vector (+1,−1,0,0).
Cartesian coordinates
The Cartesian coordinates of the vertices of a truncated 24-cell having edge length sqrt(2) are all coordinate permutations and sign combinations of:
- (0,1,2,3)
The dual configuration has coordinates at all coordinate permutation and signs of
- (1,1,1,5)
- (1,3,3,3)
- (2,2,2,4)
Structure
The 24 cubical cells are joined via their square faces to the truncated octahedra; and the 24 truncated octahedra are joined to each other via their hexagonal faces.
Projections
The parallel projection of the truncated 24-cell into 3-dimensional space, truncated octahedron first, has the following layout:
- The projection envelope is a truncated cuboctahedron.
- Two of the truncated octahedra project onto a truncated octahedron lying in the center of the envelope.
- Six cuboidal volumes join the square faces of this central truncated octahedron to the center of the octagonal faces of the great rhombicuboctahedron. These are the images of 12 of the cubical cells, a pair of cells to each image.
- The 12 square faces of the great rhombicuboctahedron are the images of the remaining 12 cubes.
- The 6 octagonal faces of the great rhombicuboctahedron are the images of 6 of the truncated octahedra.
- The 8 (non-uniform) truncated octahedral volumes lying between the hexagonal faces of the projection envelope and the central truncated octahedron are the images of the remaining 16 truncated octahedra, a pair of cells to each image.
Images
| Coxeter plane | F4 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 
|
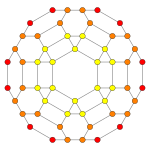
|
| Dihedral symmetry | ||
| Coxeter plane | B4 | B2 / A3 |
| Graph | 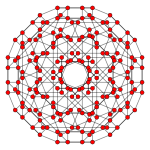
|

|
| Dihedral symmetry | ||
 Schlegel diagram (cubic cells visible) |
 Schlegel diagram 8 of 24 truncated octahedral cells visible |
 Stereographic projection Centered on truncated tetrahedron | |
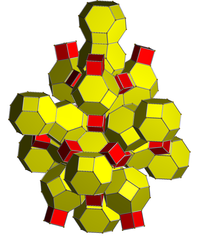 Truncated 24-cell |
 Dual to truncated 24-cell |
Related polytopes
The convex hull of the truncated 24-cell and its dual (assuming that they are congruent) is a nonuniform polychoron composed of 480 cells: 48 cubes, 144 square antiprisms, 288 tetrahedra (as tetragonal disphenoids), and 384 vertices. Its vertex figure is a hexakis triangular cupola.
Bitruncated 24-cell
| Bitruncated 24-cell | ||
|---|---|---|
 Schlegel diagram, centered on truncated cube, with alternate cells hidden | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | 2t{3,4,3} | |
| Coxeter diagram | ||
| Cells | 48 (3.8.8) | |
| Faces | 336 | 192 {3} 144 {8} |
| Edges | 576 | |
| Vertices | 288 | |
| Edge figure | 3.8.8 | |
| Vertex figure |  tetragonal disphenoid | |
| dual polytope | Disphenoidal 288-cell | |
| Symmetry group | Aut(F4), ], order 2304 | |
| Properties | convex, isogonal, isotoxal, isochoric | |
| Uniform index | 26 27 28 | |
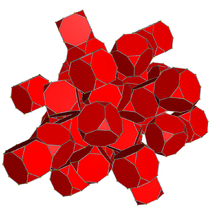
The bitruncated 24-cell. 48-cell, or tetracontoctachoron is a 4-dimensional uniform polytope (or uniform 4-polytope) derived from the 24-cell.
E. L. Elte identified it in 1912 as a semiregular polytope.
It is constructed by bitruncating the 24-cell (truncating at halfway to the depth which would yield the dual 24-cell).
Being a uniform 4-polytope, it is vertex-transitive. In addition, it is cell-transitive, consisting of 48 truncated cubes, and also edge-transitive, with 3 truncated cubes cells per edge and with one triangle and two octagons around each edge.
The 48 cells of the bitruncated 24-cell correspond with the 24 cells and 24 vertices of the 24-cell. As such, the centers of the 48 cells form the root system of type F4.
Its vertex figure is a tetragonal disphenoid, a tetrahedron with 2 opposite edges length 1 and all 4 lateral edges length √(2+√2).
Alternative names
- Bitruncated 24-cell (Norman W. Johnson)
- 48-cell as a cell-transitive 4-polytope
- Bitruncated icositetrachoron
- Bitruncated polyoctahedron
- Tetracontaoctachoron (Cont) (Jonathan Bowers)
Structure
The truncated cubes are joined to each other via their octagonal faces in anti orientation; i. e., two adjoining truncated cubes are rotated 45 degrees relative to each other so that no two triangular faces share an edge.
The sequence of truncated cubes joined to each other via opposite octagonal faces form a cycle of 8. Each truncated cube belongs to 3 such cycles. On the other hand, the sequence of truncated cubes joined to each other via opposite triangular faces form a cycle of 6. Each truncated cube belongs to 4 such cycles.
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time. Edges exist at 4 symmetry positions. Squares exist at 3 positions, hexagons 2 positions, and octagons one. Finally the 4 types of cells exist centered on the 4 corners of the fundamental simplex.
| F4 | k-face | fk | f0 | f1 | f2 | f3 | k-figure | Notes | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1A1 | ( ) | f0 | 288 | 2 | 2 | 1 | 4 | 1 | 2 | 2 | s{2,4} | F4/A1A1 = 288 | |
| { } | f1 | 2 | 288 | * | 1 | 2 | 0 | 2 | 1 | { }v( ) | |||
| 2 | * | 288 | 0 | 2 | 1 | 1 | 2 | ||||||
| A2A1 | {3} | f2 | 3 | 3 | 0 | 96 | * | * | 2 | 0 | { } | F4/A2A1 = 1152/6/2 = 96 | |
| B2 | t{4} | 8 | 4 | 4 | * | 144 | * | 1 | 1 | F4/B2 = 1152/8 = 144 | |||
| A2A1 | {3} | 3 | 0 | 3 | * | * | 96 | 0 | 2 | F4/A2A1 = 1152/6/2 = 96 | |||
| B3 | t{4,3} | f3 | 24 | 24 | 12 | 8 | 6 | 0 | 24 | * | ( ) | F4/B3 = 1152/48 = 24 | |
| 24 | 12 | 24 | 0 | 6 | 8 | * | 24 | ||||||
Coordinates
The Cartesian coordinates of a bitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:
- (0, 2+√2, 2+√2, 2+2√2)
- (1, 1+√2, 1+√2, 3+2√2)
Projections
Projection to 2 dimensions
| Coxeter plane | F4 | B4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ] = | |
| Coxeter plane | B3 / A2 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | ] = |
Projection to 3 dimensions
| Orthographic | Perspective |
|---|---|
The following animation shows the orthographic projection of the bitruncated 24-cell into 3 dimensions. The animation itself is a perspective projection from the static 3D image into 2D, with rotation added to make its structure more apparent. The images of the 48 truncated cubes are laid out as follows:
|
The following animation shows the cell-first perspective projection of the bitruncated 24-cell into 3 dimensions. Its structure is the same as the previous animation, except that there is some foreshortening due to the perspective projection. |

|
Related regular skew polyhedron
The regular skew polyhedron, {8,4|3}, exists in 4-space with 4 octagonal around each vertex, in a zig-zagging nonplanar vertex figure. These octagonal faces can be seen on the bitruncated 24-cell, using all 576 edges and 288 vertices. The 192 triangular faces of the bitruncated 24-cell can be seen as removed. The dual regular skew polyhedron, {4,8|3}, is similarly related to the square faces of the runcinated 24-cell.
Disphenoidal 288-cell
| Disphenoidal 288-cell | ||
|---|---|---|
| Type | perfect polychoron | |
| Symbol | f1,2F4 (1,0,0,0)F4 ⊕ (0,0,0,1)F4 | |
| Coxeter | ||
| Cells |  288 congruent tetragonal disphenoids | |
| Faces | 576 congruent isosceles (2 short edges) | |
| Edges | 336 | 192 of length 144 of length |
| Vertices | 48 | |
| Vertex figure |  (Triakis octahedron) | |
| Dual | Bitruncated 24-cell | |
| Coxeter group | Aut(F4), ], order 2304 | |
| Orbit vector | (1, 2, 1, 1) | |
| Properties | convex, isochoric | |
The disphenoidal 288-cell is the dual of the bitruncated 24-cell. It is a 4-dimensional polytope (or polychoron) derived from the 24-cell. It is constructed by doubling and rotating the 24-cell, then constructing the convex hull.
Being the dual of a uniform polychoron, it is cell-transitive, consisting of 288 congruent tetragonal disphenoids. In addition, it is vertex-transitive under the group Aut(F4).
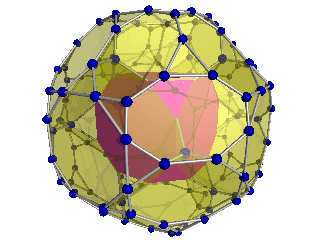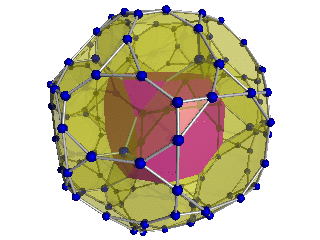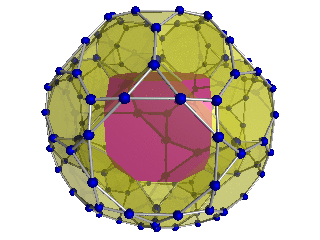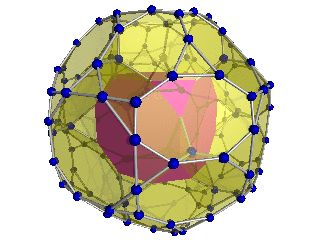
Images
| Coxeter planes | B2 | B3 | F4 |
|---|---|---|---|
| Disphenoidal 288-cell |

|

| |
| Bitruncated 24-cell |

|
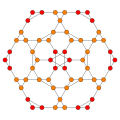
|

|
Geometry
The vertices of the 288-cell are precisely the 24 Hurwitz unit quaternions with norm squared 1, united with the 24 vertices of the dual 24-cell with norm squared 2, projected to the unit 3-sphere. These 48 vertices correspond to the binary octahedral group 2O or <2,3,4>, order 48.
Thus, the 288-cell is the only non-regular 4-polytope which is the convex hull of a quaternionic group, disregarding the infinitely many dicyclic (same as binary dihedral) groups; the regular ones are the 24-cell (≘ 2T or <2,3,3>, order 24) and the 600-cell (≘ 2I or <2,3,5>, order 120). (The 16-cell corresponds to the binary dihedral group 2D2 or <2,2,2>, order 16.)
The inscribed 3-sphere has radius 1/2+√2/4 ≈ 0.853553 and touches the 288-cell at the centers of the 288 tetrahedra which are the vertices of the dual bitruncated 24-cell.
The vertices can be coloured in 2 colours, say red and yellow, with the 24 Hurwitz units in red and the 24 duals in yellow, the yellow 24-cell being congruent to the red one. Thus the product of 2 equally coloured quaternions is red and the product of 2 in mixed colours is yellow.
| Region | Layer | Latitude | red | yellow | ||
|---|---|---|---|---|---|---|
| Northern hemisphere | 3 | 1 | 1 | 0 | ||
| 2 | √2/2 | 0 | 6 | |||
| 1 | 1/2 | 8 | 0 | |||
| Equator | 0 | 0 | 6 | 12 | ||
| Southern hemisphere | –1 | –1/2 | 8 | 0 | ||
| –2 | –√2/2 | 0 | 6 | |||
| –3 | –1 | 1 | 0 | |||
| Total | 24 | 24 | ||||
Placing a fixed red vertex at the north pole (1,0,0,0), there are 6 yellow vertices in the next deeper “latitude” at (√2/2,x,y,z), followed by 8 red vertices in the latitude at (1/2,x,y,z). The complete coordinates are given as linear combinations of the quaternionic units , which at the same time can be taken as the elements of the group 2O. The next deeper latitude is the equator hyperplane intersecting the 3-sphere in a 2-sphere which is populated by 6 red and 12 yellow vertices.
Layer 2 is a 2-sphere circumscribing a regular octahedron whose edges have length 1. A tetrahedron with vertex north pole has 1 of these edges as long edge whose 2 vertices are connected by short edges to the north pole. Another long edge runs from the north pole into layer 1 and 2 short edges from there into layer 2.
There are 192 long edges with length 1 connecting equal colours and 144 short edges with length √2–√2 ≈ 0.765367 connecting mixed colours. 192*2/48 = 8 long and 144*2/48 = 6 short, that is together 14 edges meet at any vertex.
The 576 faces are isosceles with 1 long and 2 short edges, all congruent. The angles at the base are arccos(√4+√8/4) ≈ 49.210°. 576*3/48 = 36 faces meet at a vertex, 576*1/192 = 3 at a long edge, and 576*2/144 = 8 at a short one.
The 288 cells are tetrahedra with 4 short edges and 2 antipodal and perpendicular long edges, one of which connects 2 red and the other 2 yellow vertices. All the cells are congruent. 288*4/48 = 24 cells meet at a vertex. 288*2/192 = 3 cells meet at a long edge, 288*4/144 = 8 at a short one. 288*4/576 = 2 cells meet at a triangle.
Related polytopes
| D4 uniform polychora | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|

|
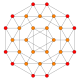
|

|

|

|
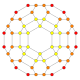
|
| ||||
| {3,3} h{4,3,3} |
2r{3,3} h3{4,3,3} |
t{3,3} h2{4,3,3} |
2t{3,3} h2,3{4,3,3} |
r{3,3} {3}={3,4,3} |
rr{3,3} r{3}=r{3,4,3} |
tr{3,3} t{3}=t{3,4,3} |
sr{3,3} s{3}=s{3,4,3} | ||||
B4 family of uniform polytopes:
| B4 symmetry polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | tesseract | rectified tesseract |
truncated tesseract |
cantellated tesseract |
runcinated tesseract |
bitruncated tesseract |
cantitruncated tesseract |
runcitruncated tesseract |
omnitruncated tesseract | ||
| Coxeter diagram |
= |
= |
|||||||||
| Schläfli symbol |
{4,3,3} | t1{4,3,3} r{4,3,3} |
t0,1{4,3,3} t{4,3,3} |
t0,2{4,3,3} rr{4,3,3} |
t0,3{4,3,3} | t1,2{4,3,3} 2t{4,3,3} |
t0,1,2{4,3,3} tr{4,3,3} |
t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegel diagram |

|

|
|

|

|

|
|
|

| ||
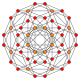
| B4 | 
|

|

|

|
|

|

|
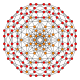
|

| ||
| Name | 16-cell | rectified 16-cell |
truncated 16-cell |
cantellated 16-cell |
runcinated 16-cell |
bitruncated 16-cell |
cantitruncated 16-cell |
runcitruncated 16-cell |
omnitruncated 16-cell | ||
| Coxeter diagram |
= |
= |
= |
= |
= |
= |
|||||
| Schläfli symbol |
{3,3,4} | t1{3,3,4} r{3,3,4} |
t0,1{3,3,4} t{3,3,4} |
t0,2{3,3,4} rr{3,3,4} |
t0,3{3,3,4} | t1,2{3,3,4} 2t{3,3,4} |
t0,1,2{3,3,4} tr{3,3,4} |
t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegel diagram |
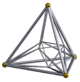
|

|

|

|

|
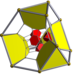
|

|
|

| ||
| B4 | 
|

|

|

|

|

|

|

|

| ||
F4 family of uniform polytopes:
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
| Schlegel diagram |

|

|

|

|

|

|

|

|

|

| |
| F4 | 
|

|

|

|

|

|

|

|

|

| |
| B4 | 
|

|

|

|
|

|

|

|

|

| |
| B3(a) | 
|

|

|

|

|

|

|

|
|

| |
| B3(b) | 
|

|

|
|

|
| |||||
| B2 | 
|

|

|

|

|

|

|
|
|

| |
References
- Klitzing, Richard. "o3x4x3o - cont".
- ^ On Perfect 4-Polytopes Gabor Gévay Contributions to Algebra and Geometry Volume 43 (2002), No. 1, 243-259 ] Table 2, page 252
- ^ Quaternionic Construction of the W(F4) Polytopes with Their Dual Polytopes and Branching under the Subgroups W(B4) and W(B3) × W(A1) Mehmet Koca 1, Mudhahir Al-Ajmi 2 and Nazife Ozdes Koca 3 Department of Physics, College of Science, Sultan Qaboos University P. O. Box 36, Al-Khoud 123, Muscat, Sultanate of Oman, p.18. 5.7 Dual polytope of the polytope (0, 1, 1, 0)F4 = W(F4)(ω2+ω3)
- H.S.M. Coxeter:
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Klitzing, Richard. "4D uniform polytopes (polychora)". x3x4o3o=x3x3x4o - tico, o3x4x3o - cont
- 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 24, 27, George Olshevsky.


 =
=
 =
=
 =
=










 , which at the same time can be taken as the elements of the group 2O. The next deeper latitude is the equator hyperplane intersecting the 3-sphere in a 2-sphere which is populated by 6 red and 12 yellow vertices.
, which at the same time can be taken as the elements of the group 2O. The next deeper latitude is the equator hyperplane intersecting the 3-sphere in a 2-sphere which is populated by 6 red and 12 yellow vertices.