| Parts of this article (those related to computer science) need to be updated. The reason given is: Some information are outdated and referred to the past years. Please help update this article to reflect recent events or newly available information. (March 2024) |
Asynchronous circuit (clockless or self-timed circuit) is a sequential digital logic circuit that does not use a global clock circuit or signal generator to synchronize its components. Instead, the components are driven by a handshaking circuit which indicates a completion of a set of instructions. Handshaking works by simple data transfer protocols. Many synchronous circuits were developed in early 1950s as part of bigger asynchronous systems (e.g. ORDVAC). Asynchronous circuits and theory surrounding is a part of several steps in integrated circuit design, a field of digital electronics engineering.
Asynchronous circuits are contrasted with synchronous circuits, in which changes to the signal values in the circuit are triggered by repetitive pulses called a clock signal. Most digital devices today use synchronous circuits. However asynchronous circuits have a potential to be much faster, have a lower level of power consumption, electromagnetic interference, and better modularity in large systems. Asynchronous circuits are an active area of research in digital logic design.
It was not until the 1990s when viability of the asynchronous circuits was shown by real-life commercial products.
Overview
All digital logic circuits can be divided into combinational logic, in which the output signals depend only on the current input signals, and sequential logic, in which the output depends both on current input and on past inputs. In other words, sequential logic is combinational logic with memory. Virtually all practical digital devices require sequential logic. Sequential logic can be divided into two types, synchronous logic and asynchronous logic.
Synchronous circuits
In synchronous logic circuits, an electronic oscillator generates a repetitive series of equally spaced pulses called the clock signal. The clock signal is supplied to all the components of the IC. Flip-flops only flip when triggered by the edge of the clock pulse, so changes to the logic signals throughout the circuit begin at the same time and at regular intervals. The output of all memory elements in a circuit is called the state of the circuit. The state of a synchronous circuit changes only on the clock pulse. The changes in signal require a certain amount of time to propagate through the combinational logic gates of the circuit. This time is called a propagation delay.
As of 2021, timing of modern synchronous ICs takes significant engineering efforts and sophisticated design automation tools. Designers have to ensure that clock arrival is not faulty. With the ever-growing size and complexity of ICs (e.g. ASICs) it's a challenging task. In huge circuits, signals sent over clock distribution network often end up at different times at different parts. This problem is widely known as "clock skew".
The maximum possible clock rate is capped by the logic path with the longest propagation delay, called the critical path. Because of that, the paths that may operate quickly are idle most of the time. A widely distributed clock network dissipates a lot of useful power and must run whether the circuit is receiving inputs or not. Because of this level of complexity, testing and debugging takes over half of development time in all dimensions for synchronous circuits.
Asynchronous circuits
The asynchronous circuits do not need a global clock, and the state of the circuit changes as soon as the inputs change. The local functional blocks may be still employed but the clock skew problem still can be tolerated.
Since asynchronous circuits do not have to wait for a clock pulse to begin processing inputs, they can operate faster. Their speed is theoretically limited only by the propagation delays of the logic gates and other elements.
However, asynchronous circuits are more difficult to design and subject to problems not found in synchronous circuits. This is because the resulting state of an asynchronous circuit can be sensitive to the relative arrival times of inputs at gates. If transitions on two inputs arrive at almost the same time, the circuit can go into the wrong state depending on slight differences in the propagation delays of the gates.
This is called a race condition. In synchronous circuits this problem is less severe because race conditions can only occur due to inputs from outside the synchronous system, called asynchronous inputs.
Although some fully asynchronous digital systems have been built (see below), today asynchronous circuits are typically used in a few critical parts of otherwise synchronous systems where speed is at a premium, such as signal processing circuits.
Theoretical foundation
The original theory of asynchronous circuits was created by David E. Muller in mid-1950s. This theory was presented later in the well-known book "Switching Theory" by Raymond Miller.
The term "asynchronous logic" is used to describe a variety of design styles, which use different assumptions about circuit properties. These vary from the bundled delay model – which uses "conventional" data processing elements with completion indicated by a locally generated delay model – to delay-insensitive design – where arbitrary delays through circuit elements can be accommodated. The latter style tends to yield circuits which are larger than bundled data implementations, but which are insensitive to layout and parametric variations and are thus "correct by design".
Asynchronous logic
Asynchronous logic is the logic required for the design of asynchronous digital systems. These function without a clock signal and so individual logic elements cannot be relied upon to have a discrete true/false state at any given time. Boolean (two valued) logic is inadequate for this and so extensions are required.
Since 1984, Vadim O. Vasyukevich developed an approach based upon new logical operations which he called venjunction (with asynchronous operator "x∠y" standing for "switching x on the background y" or "if x when y then") and sequention (with priority signs "xi≻xj" and "xi≺xj"). This takes into account not only the current value of an element, but also its history.
Karl M. Fant developed a different theoretical treatment of asynchronous logic in his work Logically determined design in 2005 which used four-valued logic with null and intermediate being the additional values. This architecture is important because it is quasi-delay-insensitive. Scott C. Smith and Jia Di developed an ultra-low-power variation of Fant's Null Convention Logic that incorporates multi-threshold CMOS. This variation is termed Multi-threshold Null Convention Logic (MTNCL), or alternatively Sleep Convention Logic (SCL).
Petri nets
Petri nets are an attractive and powerful model for reasoning about asynchronous circuits (see Subsequent models of concurrency). A particularly useful type of interpreted Petri nets, called Signal Transition Graphs (STGs), was proposed independently in 1985 by Leonid Rosenblum and Alex Yakovlev and Tam-Anh Chu. Since then, STGs have been studied extensively in theory and practice, which has led to the development of popular software tools for analysis and synthesis of asynchronous control circuits, such as Petrify and Workcraft.
Subsequent to Petri nets other models of concurrency have been developed that can model asynchronous circuits including the Actor model and process calculi.
Benefits
A variety of advantages have been demonstrated by asynchronous circuits. Both quasi-delay-insensitive (QDI) circuits (generally agreed to be the most "pure" form of asynchronous logic that retains computational universality) and less pure forms of asynchronous circuitry which use timing constraints for higher performance and lower area and power present several advantages.
- Robust and cheap handling of metastability of arbiters.
- Average-case performance: an average-case time (delay) of operation is not limited to the worst-case completion time of component (gate, wire, block etc.) as it is in synchronous circuits. This results in better latency and throughput performance. Examples include speculative completion which has been applied to design parallel prefix adders faster than synchronous ones, and a high-performance double-precision floating point adder which outperforms leading synchronous designs.
- Early completion: the output may be generated ahead of time, when result of input processing is predictable or irrelevant.
- Inherent elasticity: variable number of data items may appear in pipeline inputs at any time (pipeline means a cascade of linked functional blocks). This contributes to high performance while gracefully handling variable input and output rates due to unclocked pipeline stages (functional blocks) delays (congestions may still be possible however and input-output gates delay should be also taken into account).
- No need for timing-matching between functional blocks either. Though given different delay models (predictions of gate/wire delay times) this depends on actual approach of asynchronous circuit implementation.
- Freedom from the ever-worsening difficulties of distributing a high-fan-out, timing-sensitive clock signal.
- Circuit speed adapts to changing temperature and voltage conditions rather than being locked at the speed mandated by worst-case assumptions.
- Lower, on-demand power consumption; zero standby power consumption. In 2005 Epson has reported 70% lower power consumption compared to synchronous design. Also, clock drivers can be removed which can significantly reduce power consumption. However, when using certain encodings, asynchronous circuits may require more area, adding similar power overhead if the underlying process has poor leakage properties (for example, deep submicrometer processes used prior to the introduction of high-κ dielectrics).
- No need for power-matching between local asynchronous functional domains of circuitry. Synchronous circuits tend to draw a large amount of current right at the clock edge and shortly thereafter. The number of nodes switching (and hence, the amount of current drawn) drops off rapidly after the clock edge, reaching zero just before the next clock edge. In an asynchronous circuit, the switching times of the nodes does not correlated in this manner, so the current draw tends to be more uniform and less bursty.
- Robustness toward transistor-to-transistor variability in the manufacturing transfer process (which is one of the most serious problems facing the semiconductor industry as dies shrink), variations of voltage supply, temperature, and fabrication process parameters.
- Less severe electromagnetic interference (EMI). Synchronous circuits create a great deal of EMI in the frequency band at (or very near) their clock frequency and its harmonics; asynchronous circuits generate EMI patterns which are much more evenly spread across the spectrum.
- Design modularity (reuse), improved noise immunity and electromagnetic compatibility. Asynchronous circuits are more tolerant to process variations and external voltage fluctuations.
Disadvantages
- Area overhead caused by additional logic implementing handshaking. In some cases an asynchronous design may require up to double the resources (area, circuit speed, power consumption) of a synchronous design, due to addition of completion detection and design-for-test circuits.
- Compared to a synchronous design, as of the 1990s and early 2000s not many people are trained or experienced in the design of asynchronous circuits.
- Synchronous designs are inherently easier to test and debug than asynchronous designs. However, this position is disputed by Fant, who claims that the apparent simplicity of synchronous logic is an artifact of the mathematical models used by the common design approaches.
- Clock gating in more conventional synchronous designs is an approximation of the asynchronous ideal, and in some cases, its simplicity may outweigh the advantages of a fully asynchronous design.
- Performance (speed) of asynchronous circuits may be reduced in architectures that require input-completeness (more complex data path).
- Lack of dedicated, asynchronous design-focused commercial EDA tools. As of 2006 the situation was slowly improving, however.
Communication
There are several ways to create asynchronous communication channels that can be classified by their protocol and data encoding.
Protocols
There are two widely used protocol families which differ in the way communications are encoded:
- two-phase handshake (also known as two-phase protocol, Non-Return-to-Zero (NRZ) encoding, or transition signaling): Communications are represented by any wire transition; transitions from 0 to 1 and from 1 to 0 both count as communications.
- four-phase handshake (also known as four-phase protocol, or Return-to-Zero (RZ) encoding): Communications are represented by a wire transition followed by a reset; a transition sequence from 0 to 1 and back to 0 counts as single communication.

Despite involving more transitions per communication, circuits implementing four-phase protocols are usually faster and simpler than two-phase protocols because the signal lines return to their original state by the end of each communication. In two-phase protocols, the circuit implementations would have to store the state of the signal line internally.
Note that these basic distinctions do not account for the wide variety of protocols. These protocols may encode only requests and acknowledgements or also encode the data, which leads to the popular multi-wire data encoding. Many other, less common protocols have been proposed including using a single wire for request and acknowledgment, using several significant voltages, using only pulses or balancing timings in order to remove the latches.
Data encoding
There are two widely used data encodings in asynchronous circuits: bundled-data encoding and multi-rail encoding
Another common way to encode the data is to use multiple wires to encode a single digit: the value is determined by the wire on which the event occurs. This avoids some of the delay assumptions necessary with bundled-data encoding, since the request and the data are not separated anymore.
Bundled-data encoding
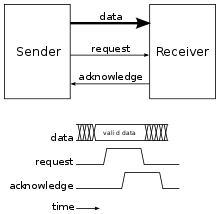
Bundled-data encoding uses one wire per bit of data with a request and an acknowledge signal; this is the same encoding used in synchronous circuits without the restriction that transitions occur on a clock edge. The request and the acknowledge are sent on separate wires with one of the above protocols. These circuits usually assume a bounded delay model with the completion signals delayed long enough for the calculations to take place.
In operation, the sender signals the availability and validity of data with a request. The receiver then indicates completion with an acknowledgement, indicating that it is able to process new requests. That is, the request is bundled with the data, hence the name "bundled-data".
Bundled-data circuits are often referred to as micropipelines, whether they use a two-phase or four-phase protocol, even if the term was initially introduced for two-phase bundled-data.
Multi-rail encoding
Multi-rail encoding uses multiple wires without a one-to-one relationship between bits and wires and a separate acknowledge signal. Data availability is indicated by the transitions themselves on one or more of the data wires (depending on the type of multi-rail encoding) instead of with a request signal as in the bundled-data encoding. This provides the advantage that the data communication is delay-insensitive. Two common multi-rail encodings are one-hot and dual rail. The one-hot (also known as 1-of-n) encoding represents a number in base n with a communication on one of the n wires. The dual-rail encoding uses pairs of wires to represent each bit of the data, hence the name "dual-rail"; one wire in the pair represents the bit value of 0 and the other represents the bit value of 1. For example, a dual-rail encoded two bit number will be represented with two pairs of wires for four wires in total. During a data communication, communications occur on one of each pair of wires to indicate the data's bits. In the general case, an m n encoding represent data as m words of base n.

Dual-rail encoding
Dual-rail encoding with a four-phase protocol is the most common and is also called three-state encoding, since it has two valid states (10 and 01, after a transition) and a reset state (00). Another common encoding, which leads to a simpler implementation than one-hot, two-phase dual-rail is four-state encoding, or level-encoded dual-rail, and uses a data bit and a parity bit to achieve a two-phase protocol.
Asynchronous CPU
Asynchronous CPUs are one of several ideas for radically changing CPU design.
Unlike a conventional processor, a clockless processor (asynchronous CPU) has no central clock to coordinate the progress of data through the pipeline. Instead, stages of the CPU are coordinated using logic devices called "pipeline controls" or "FIFO sequencers". Basically, the pipeline controller clocks the next stage of logic when the existing stage is complete. In this way, a central clock is unnecessary. It may actually be even easier to implement high performance devices in asynchronous, as opposed to clocked, logic:
- components can run at different speeds on an asynchronous CPU; all major components of a clocked CPU must remain synchronized with the central clock;
- a traditional CPU cannot "go faster" than the expected worst-case performance of the slowest stage/instruction/component. When an asynchronous CPU completes an operation more quickly than anticipated, the next stage can immediately begin processing the results, rather than waiting for synchronization with a central clock. An operation might finish faster than normal because of attributes of the data being processed (e.g., multiplication can be very fast when multiplying by 0 or 1, even when running code produced by a naive compiler), or because of the presence of a higher voltage or bus speed setting, or a lower ambient temperature, than 'normal' or expected.
Asynchronous logic proponents believe these capabilities would have these benefits:
- lower power dissipation for a given performance level, and
- highest possible execution speeds.
The biggest disadvantage of the clockless CPU is that most CPU design tools assume a clocked CPU (i.e., a synchronous circuit). Many tools "enforce synchronous design practices". Making a clockless CPU (designing an asynchronous circuit) involves modifying the design tools to handle clockless logic and doing extra testing to ensure the design avoids metastable problems. The group that designed the AMULET, for example, developed a tool called LARD to cope with the complex design of AMULET3.
Examples
Despite all the difficulties numerous asynchronous CPUs have been built.
The ORDVAC of 1951 was a successor to the ENIAC and the first asynchronous computer ever built.
The ILLIAC II was the first completely asynchronous, speed independent processor design ever built; it was the most powerful computer at the time.
DEC PDP-16 Register Transfer Modules (ca. 1973) allowed the experimenter to construct asynchronous, 16-bit processing elements. Delays for each module were fixed and based on the module's worst-case timing.
Caltech
Since the mid-1980s, Caltech has designed four non-commercial CPUs in attempt to evaluate performance and energy efficiency of the asynchronous circuits.
- Caltech Asynchronous Microprocessor (CAM)
In 1988 the Caltech Asynchronous Microprocessor (CAM) was the first asynchronous, quasi delay-insensitive (QDI) microprocessor made by Caltech. The processor had 16-bit wide RISC ISA and separate instruction and data memories. It was manufactured by MOSIS and funded by DARPA. The project was supervised by the Office of Naval Research, the Army Research Office, and the Air Force Office of Scientific Research.
During demonstrations, the researchers loaded a simple program which ran in a tight loop, pulsing one of the output lines after each instruction. This output line was connected to an oscilloscope. When a cup of hot coffee was placed on the chip, the pulse rate (the effective "clock rate") naturally slowed down to adapt to the worsening performance of the heated transistors. When liquid nitrogen was poured on the chip, the instruction rate shot up with no additional intervention. Additionally, at lower temperatures, the voltage supplied to the chip could be safely increased, which also improved the instruction rate – again, with no additional configuration.
When implemented in gallium arsenide (HGaAs
3) it was claimed to achieve 100MIPS. Overall, the research paper interpreted the resultant performance of CAM as superior compared to commercial alternatives available at the time.
- MiniMIPS
In 1998 the MiniMIPS, an experimental, asynchronous MIPS I-based microcontroller was made. Even though its SPICE-predicted performance was around 280 MIPS at 3.3 V the implementation suffered from several mistakes in layout (human mistake) and the results turned out be lower by about 40% (see table).
- The Lutonium 8051
Made in 2003, it was a quasi delay-insensitive asynchronous microcontroller designed for energy efficiency. The microcontroller's implementation followed the Harvard architecture.
| Name | Year | Word size (bits) | Transistors (thousands) | Size (mm) | Node size (μm) | 1.5V | 2V | 3.3V | 5V | 10V |
|---|---|---|---|---|---|---|---|---|---|---|
| CAM SCMOS | 1988 | 16 | 20 | N/A | 1.6 | N/A | 5 | N/A | 18 | 26 |
| MiniMIPS CMOS | 1998 | 32 | 2000 | 8×14 | 0.6 | 60 | 100 | 180 | N/A | N/A |
| Lutonium 8051 CMOS | 2003 | 8 | N/A | N/A | 0.18 | 200 | N/A | N/A | N/A | 4 |
Epson
In 2004, Epson manufactured the world's first bendable microprocessor called ACT11, an 8-bit asynchronous chip. Synchronous flexible processors are slower, since bending the material on which a chip is fabricated causes wild and unpredictable variations in the delays of various transistors, for which worst-case scenarios must be assumed everywhere and everything must be clocked at worst-case speed. The processor is intended for use in smart cards, whose chips are currently limited in size to those small enough that they can remain perfectly rigid.
IBM
In 2014, IBM announced a SyNAPSE-developed chip that runs in an asynchronous manner, with one of the highest transistor counts of any chip ever produced. IBM's chip consumes orders of magnitude less power than traditional computing systems on pattern recognition benchmarks.
Timeline
- ORDVAC and the (identical) ILLIAC I (1951)
- Johnniac (1953)
- WEIZAC (1955)
- Kiev (1958), a Soviet machine using the programming language with pointers much earlier than they came to the PL/1 language
- ILLIAC II (1962)
- Victoria University of Manchester built Atlas (1964)
- ICL 1906A and 1906S mainframe computers, part of the 1900 series and sold from 1964 for over a decade by ICL
- Polish computers KAR-65 and K-202 (1965 and 1970 respectively)
- Honeywell CPUs 6180 (1972) and Series 60 Level 68 (1981) upon which Multics ran asynchronously
- Soviet bit-slice microprocessor modules (late 1970s) produced as К587, К588 and К1883 (U83x in East Germany)
- Caltech Asynchronous Microprocessor, the world-first asynchronous microprocessor (1988)
- ARM-implementing AMULET (1993 and 2000)
- Asynchronous implementation of MIPS R3000, dubbed MiniMIPS (1998)
- Several versions of the XAP processor experimented with different asynchronous design styles: a bundled data XAP, a 1-of-4 XAP, and a 1-of-2 (dual-rail) XAP (2003?)
- ARM-compatible processor (2003?) designed by Z. C. Yu, S. B. Furber, and L. A. Plana; "designed specifically to explore the benefits of asynchronous design for security sensitive applications"
- SAMIPS (2003), a synthesisable asynchronous implementation of the MIPS R3000 processor
- "Network-based Asynchronous Architecture" processor (2005) that executes a subset of the MIPS architecture instruction set
- ARM996HS processor (2006) from Handshake Solutions
- HT80C51 processor (2007?) from Handshake Solutions.
- Vortex, a superscalar general purpose CPU with a load/store architecture from Intel (2007); it was developed as Fulcrum Microsystem test Chip 2 and was not commercialized, excepting some of its components; the chip included DDR SDRAM and a 10Gb Ethernet interface linked via Nexus system-on-chip net to the CPU
- SEAforth multi-core processor (2008) from Charles H. Moore
- GA144 multi-core processor (2010) from Charles H. Moore
- TAM16: 16-bit asynchronous microcontroller IP core (Tiempo)
- Aspida asynchronous DLX core; the asynchronous open-source DLX processor (ASPIDA) has been successfully implemented both in ASIC and FPGA versions
See also
- Adiabatic logic
- Event camera (asynchronous camera)
- Perfect clock gating
- Petri nets
- Sequential logic (asynchronous)
- Signal transition graphs
Notes
- Globally asynchronous locally synchronous circuits are possible.
- Dhrystone was also used.
References
- ^ Horowitz, Mark (2007). "Advanced VLSI Circuit Design Lecture". Stanford University, Computer Systems Laboratory. Archived from the original on 2016-04-21.
- Staunstrup, Jørgen (1994). A Formal Approach to Hardware Design. Boston, Massachusetts, USA: Springer USA. ISBN 978-1-4615-2764-0. OCLC 852790160.
- ^ Sparsø, Jens (April 2006). "Asynchronous Circuit Design A Tutorial" (PDF). Technical University of Denmark.
- Nowick, S. M.; Singh, M. (May–June 2015). "Asynchronous Design — Part 1: Overview and Recent Advances" (PDF). IEEE Design and Test. 32 (3): 5–18. doi:10.1109/MDAT.2015.2413759. S2CID 14644656. Archived from the original (PDF) on 2018-12-21. Retrieved 2019-08-27.
- Nowick, S. M.; Singh, M. (May–June 2015). "Asynchronous Design — Part 2: Systems and Methodologies" (PDF). IEEE Design and Test. 32 (3): 19–28. doi:10.1109/MDAT.2015.2413757. S2CID 16732793. Archived from the original (PDF) on 2018-12-21. Retrieved 2019-08-27.
- ^ "Why Asynchronous Design?". Galois, Inc. 2021-07-15. Retrieved 2021-12-04.
- ^ Myers, Chris J. (2001). Asynchronous circuit design. New York: J. Wiley & Sons. ISBN 0-471-46412-0. OCLC 53227301.
- Muller, D. E. (1955). Theory of asynchronous circuits, Report no. 66. Digital Computer Laboratory, University of Illinois at Urbana-Champaign.
- Miller, Raymond E. (1965). Switching Theory, Vol. II. Wiley.
- van Berkel, C. H.; Josephs, M. B.; Nowick, S. M. (February 1999). "Applications of Asynchronous Circuits" (PDF). Proceedings of the IEEE. 87 (2): 234–242. doi:10.1109/5.740016. Archived from the original (PDF) on 2018-04-03. Retrieved 2019-08-27.
- Vasyukevich, Vadim O. (1984). "Whenjunction as a logic/dynamic operation. Definition, implementation and applications". Automatic Control and Computer Sciences. 18 (6): 68–74. (NB. The function was still called whenjunction instead of venjunction in this publication.)
- Vasyukevich, Vadim O. (1998). "Monotone sequences of binary data sets and their identification by means of venjunctive functions". Automatic Control and Computer Sciences. 32 (5): 49–56.
- Vasyukevich, Vadim O. (April 2007). "Decoding asynchronous sequences". Automatic Control and Computer Sciences. 41 (2). Allerton Press: 93–99. doi:10.3103/S0146411607020058. ISSN 1558-108X. S2CID 21204394.
- Vasyukevich, Vadim O. (2009). "Asynchronous logic elements. Venjunction and sequention" (PDF). Archived (PDF) from the original on 2011-07-22. (118 pages)
- Vasyukevich, Vadim O. (2011). Written at Riga, Latvia. Asynchronous Operators of Sequential Logic: Venjunction & Sequention — Digital Circuits Analysis and Design. Lecture Notes in Electrical Engineering. Vol. 101 (1st ed.). Berlin / Heidelberg, Germany: Springer-Verlag. doi:10.1007/978-3-642-21611-4. ISBN 978-3-642-21610-7. ISSN 1876-1100. LCCN 2011929655. (xiii+1+123+7 pages) (NB. The back cover of this book erroneously states volume 4, whereas it actually is volume 101.)
- Fant, Karl M. (February 2005). Logically determined design: clockless system design with NULL convention logic (NCL) (1 ed.). Hoboken, New Jersey, USA: Wiley-Interscience / John Wiley and Sons, Inc. ISBN 978-0-471-68478-7. LCCN 2004050923. (xvi+292 pages)
- ^ Fant, Karl M. (August 2007). Computer Science Reconsidered: The Invocation Model of Process Expression (1 ed.). Hoboken, New Jersey, USA: Wiley-Interscience / John Wiley and Sons, Inc. ISBN 978-0-471-79814-9. LCCN 2006052821. Retrieved 2023-07-23. (xix+1+269 pages)
- Smith, Scott C.; Di, Jia (2009). Designing Asynchronous Circuits using NULL Conventional Logic (NCL) (PDF). Synthesis Lectures on Digital Circuits & Systems. Morgan & Claypool Publishers [d]. pp. 61–73. eISSN 1932-3174. ISBN 978-1-59829-981-6. ISSN 1932-3166. Lecture #23. Retrieved 2023-09-10; Smith, Scott C.; Di, Jia (2022) . Designing Asynchronous Circuits using NULL Conventional Logic (NCL). Synthesis Lectures on Digital Circuits & Systems. University of Arkansas, Arkansas, USA: Springer Nature Switzerland AG. doi:10.1007/978-3-031-79800-9. eISSN 1932-3174. ISBN 978-3-031-79799-6. ISSN 1932-3166. Lecture #23. Retrieved 2023-09-10. (x+86+6 pages)
- Smith, Scott C.; Di, Jia. "U.S. 7,977,972 Ultra-Low Power Multi-threshold Asychronous Circuit Design". Retrieved 2011-12-12.
- Rosenblum, L. Ya.; Yakovlev, A. V. (July 1985). "Signal Graphs: from Self-timed to Timed ones. Proceedings of International Workshop on Timed Petri Nets" (PDF). Torino, Italy: IEEE CS Press. pp. 199–207. Archived (PDF) from the original on 2003-10-23.
- Chu, T.-A. (1986-06-01). "On the models for designing VLSI asynchronous digital systems". Integration. 4 (2): 99–113. doi:10.1016/S0167-9260(86)80002-5. ISSN 0167-9260.
- Yakovlev, Alexandre; Lavagno, Luciano; Sangiovanni-Vincentelli, Alberto (1996-11-01). "A unified signal transition graph model for asynchronous control circuit synthesis". Formal Methods in System Design. 9 (3): 139–188. doi:10.1007/BF00122081. ISSN 1572-8102. S2CID 26970846.
- Cortadella, J.; Kishinevsky, M.; Kondratyev, A.; Lavagno, L.; Yakovlev, A. (2002). Logic Synthesis for Asynchronous Controllers and Interfaces. Springer Series in Advanced Microelectronics. Vol. 8. Berlin / Heidelberg, Germany: Springer Berlin Heidelberg. doi:10.1007/978-3-642-55989-1. ISBN 978-3-642-62776-7.
- "Petrify: Related publications". www.cs.upc.edu. Retrieved 2021-07-28.
- "start - Workcraft". workcraft.org. Retrieved 2021-07-28.
- ^ Nowick, S. M.; Singh, M. (September–October 2011). "High-Performance Asynchronous Pipelines: an Overview" (PDF). IEEE Design & Test of Computers. 28 (5): 8–22. doi:10.1109/mdt.2011.71. S2CID 6515750. Archived from the original (PDF) on 2021-04-21. Retrieved 2019-08-27.
- Nowick, S. M.; Yun, K. Y.; Beerel, P. A.; Dooply, A. E. (March 1997). "Speculative completion for the design of high-performance asynchronous dynamic adders" (PDF). Proceedings Third International Symposium on Advanced Research in Asynchronous Circuits and Systems. pp. 210–223. doi:10.1109/ASYNC.1997.587176. ISBN 0-8186-7922-0. S2CID 1098994. Archived from the original (PDF) on 2021-04-21. Retrieved 2019-08-27.
- Nowick, S. M. (September 1996). "Design of a Low-Latency Asynchronous Adder Using Speculative Completion" (PDF). IEE Proceedings - Computers and Digital Techniques. 143 (5): 301–307. doi:10.1049/ip-cdt:19960704 (inactive 2024-12-07). Archived from the original (PDF) on 2021-04-22. Retrieved 2019-08-27.
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) - Sheikh, B.; Manohar, R. (May 2010). "An Operand-Optimized Asynchronous IEEE 754 Double-Precision Floating-Point Adder" (PDF). Proceedings of the IEEE International Symposium on Asynchronous Circuits and Systems ('Async'): 151–162. Archived from the original (PDF) on 2021-04-21. Retrieved 2019-08-27.
- ^ Sasao, Tsutomu (1993). Logic Synthesis and Optimization. Boston, Massachusetts, USA: Springer USA. ISBN 978-1-4615-3154-8. OCLC 852788081.
- "Epson Develops the World's First Flexible 8-Bit Asynchronous Microprocessor" 2005
- ^ Furber, Steve. "Principles of Asynchronous Circuit Design" (PDF). Pg. 232. Archived from the original (PDF) on 2012-04-26. Retrieved 2011-12-13.
- "Keep It Strictly Synchronous: KISS those asynchronous-logic problems good-bye". Personal Engineering and Instrumentation News, November 1997, pages 53–55. http://www.fpga-site.com/kiss.html
- ^ van Leeuwen, T. M. (2010). Implementation and automatic generation of asynchronous scheduled dataflow graph. Delft.
- Kruger, Robert (2005-03-15). "Reality TV for FPGA design engineers!". eetimes.com. Retrieved 2020-11-11.
- LARD Archived March 6, 2005, at the Wayback Machine
- ^ "In the 1950 and 1960s, asynchronous design was used in many early mainframe computers, including the ILLIAC I and ILLIAC II ... ." Brief History of asynchronous circuit design
- ^ "The Illiac is a binary parallel asynchronous computer in which negative numbers are represented as two's complements." – final summary of "Illiac Design Techniques" 1955.
- ^ Martin, A. J.; Nystrom, M.; Wong, C. G. (November 2003). "Three generations of asynchronous microprocessors". IEEE Design & Test of Computers. 20 (6): 9–17. doi:10.1109/MDT.2003.1246159. ISSN 0740-7475. S2CID 15164301.
- ^ Martin, A. J.; Nystrom, M.; Papadantonakis, K.; Penzes, P. I.; Prakash, P.; Wong, C. G.; Chang, J.; Ko, K. S.; Lee, B.; Ou, E.; Pugh, J. (2003). "The Lutonium: A sub-nanojoule asynchronous 8051 microcontroller". Ninth International Symposium on Asynchronous Circuits and Systems, 2003. Proceedings (PDF). Vancouver, BC, Canada: IEEE Comput. Soc. pp. 14–23. doi:10.1109/ASYNC.2003.1199162. ISBN 978-0-7695-1898-5. S2CID 13866418.
- ^ Martin, Alain J. (2014-02-06). "25 Years Ago: The First Asynchronous Microprocessor". Computer Science Technical Reports. California Institute of Technology. doi:10.7907/Z9QR4V3H.
{{cite journal}}: Cite journal requires|journal=(help) - "Seiko Epson tips flexible processor via TFT technology" Archived 2010-02-01 at the Wayback Machine by Mark LaPedus 2005
- "A flexible 8b asynchronous microprocessor based on low-temperature poly-silicon TFT technology" by Karaki et al. 2005. Abstract: "A flexible 8b asynchronous microprocessor ACTII ... The power level is 30% of the synchronous counterpart."
- "Introduction of TFT R&D Activities in Seiko Epson Corporation" by Tatsuya Shimoda (2005?) has picture of "A flexible 8-bit asynchronous microprocessor, ACT11"
- "Epson Develops the World's First Flexible 8-Bit Asynchronous Microprocessor"
- "Seiko Epson details flexible microprocessor: A4 sheets of e-paper in the pipeline by Paul Kallender 2005
- "SyNAPSE program develops advanced brain-inspired chip" Archived 2014-08-10 at the Wayback Machine. August 07, 2014.
- Johnniac history written in 1968
- V. M. Glushkov and E. L. Yushchenko. Mathematical description of computer "Kiev". UkrSSR, 1962 (in Russian)
- "Computer Resurrection Issue 18".
- "Entirely asynchronous, its hundred-odd boards would send out requests, earmark the results for somebody else, swipe somebody else's signals or data, and backstab each other in all sorts of amusing ways which occasionally failed (the "op not complete" timer would go off and cause a fault). ... was no hint of an organized synchronization strategy: various "it's ready now", "ok, go", "take a cycle" pulses merely surged through the vast backpanel ANDed with appropriate state and goosed the next guy down. Not without its charms, this seemingly ad-hoc technology facilitated a substantial degree of overlap ... as well as the of the Multics address mechanism to the extant 6000 architecture in an ingenious, modular, and surprising way ... . Modification and debugging of the processor, though, were no fun." "Multics Glossary: ... 6180"
- "10/81 ... DPS 8/70M CPUs" Multics Chronology
- "The Series 60, Level 68 was just a repackaging of the 6180." Multics Hardware features: Series 60, Level 68
- A. A. Vasenkov, V. L. Dshkhunian, P. R. Mashevich, P. V. Nesterov, V. V. Telenkov, Ju. E. Chicherin, D. I. Juditsky, "Microprocessor computing system," Patent US4124890, Nov. 7, 1978
- Chapter 4.5.3 in the biography of D. I. Juditsky (in Russian)
- "Серия 587 - Collection ex-USSR Chip's". Archived from the original on 2015-07-17. Retrieved 2015-07-16.
- "Серия 588 - Collection ex-USSR Chip's". Archived from the original on 2015-07-17. Retrieved 2015-07-16.
- "Серия 1883/U830 - Collection ex-USSR Chip's". Archived from the original on 2015-07-22. Retrieved 2015-07-19.
- ^ "A Network-based Asynchronous Architecture for Cryptographic Devices" by Ljiljana Spadavecchia 2005 in section "4.10.2 Side-channel analysis of dual-rail asynchronous architectures" and section "5.5.5.1 Instruction set"
- Zhang, Qianyi; Theodoropoulos, Georgios (2024). "SAMIPS: A Synthesised Asynchronous Processor". arXiv:2409.20388 .
- Zhang, Qianyi; Theodoropoulos, Georgios (2003). "Towards an Asynchronous MIPS Processor". In Omondi, Amos; Sedukhin, Stanislav (eds.). Advances in Computer Systems Architecture. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. pp. 137–150. doi:10.1007/978-3-540-39864-6_12. ISBN 978-3-540-39864-6.
- "Handshake Solutions HT80C51" "The Handshake Solutions HT80C51 is a Low power, asynchronous 80C51 implementation using handshake technology, compatible with the standard 8051 instruction set."
- ^ Lines, Andrew (March 2007). "The Vortex: A Superscalar Asynchronous Processor". 13th IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC'07). pp. 39–48. doi:10.1109/ASYNC.2007.28. ISBN 978-0-7695-2771-0. S2CID 33189213.
- Lines, A. (2003). "Nexus: An asynchronous crossbar interconnect for synchronous system-on-chip designs". 11th Symposium on High Performance Interconnects, 2003. Proceedings. Stanford, CA, USA: IEEE Comput. Soc. pp. 2–9. doi:10.1109/CONECT.2003.1231470. ISBN 978-0-7695-2012-4. S2CID 1799204.
- SEAforth Overview Archived 2008-02-02 at the Wayback Machine "... asynchronous circuit design throughout the chip. There is no central clock with billions of dumb nodes dissipating useless power. ... the processor cores are internally asynchronous themselves."
- "GreenArrayChips" "Ultra-low-powered multi-computer chips with integrated peripherals."
- Tiempo: Asynchronous TAM16 Core IP
- "ASPIDA sync/async DLX Core". OpenCores.org. Retrieved 2014-09-05.
- "Asynchronous Open-Source DLX Processor (ASPIDA)".
Further reading
- TiDE from Handshake Solutions in The Netherlands, Commercial asynchronous circuits design tool. Commercial asynchronous ARM (ARM996HS) and 8051 (HT80C51) are available.
- An introduction to asynchronous circuit design Archived 23 June 2010 at the Wayback Machine by Davis and Nowick
- Null convention logic, a design style pioneered by Theseus Logic, who have fabricated over 20 ASICs based on their NCL08 and NCL8501 microcontroller cores
- The Status of Asynchronous Design in Industry Information Society Technologies (IST) Programme, IST-1999-29119, D. A. Edwards W. B. Toms, June 2004, via www.scism.lsbu.ac.uk
- The Red Star is a version of the MIPS R3000 implemented in asynchronous logic
- The Amulet microprocessors were asynchronous ARMs, built in the 1990s at University of Manchester, England
- The SAMIPS synthesised asynchronous MIPS R3000 processor.
- The N-Protocol developed by Navarre AsyncArt, the first commercial asynchronous design methodology for conventional FPGAs
- PGPSALM an asynchronous implementation of the 6502 microprocessor
- Caltech Async Group home page
- Tiempo: French company providing asynchronous IP and design tools
- Epson ACT11 Flexible CPU Press Release
- Newcastle upon Tyne Async Group page
External links
 Media related to Asynchronous circuits at Wikimedia Commons
Media related to Asynchronous circuits at Wikimedia Commons
 n encoding represent data as m words of base n.
n encoding represent data as m words of base n.