| Part of a series on |
| Bayesian statistics |
|---|
| Posterior = Likelihood × Prior ÷ Evidence |
| Background |
| Model building |
| Posterior approximation |
| Estimators |
| Evidence approximation |
| Model evaluation |
Bayes' theorem (alternatively Bayes' law or Bayes' rule, after Thomas Bayes) gives a mathematical rule for inverting conditional probabilities, allowing one to find the probability of a cause given its effect. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to someone of a known age to be assessed more accurately by conditioning it relative to their age, rather than assuming that the person is typical of the population as a whole. Based on Bayes' law, both the prevalence of a disease in a given population and the error rate of an infectious disease test must be taken into account to evaluate the meaning of a positive test result and avoid the base-rate fallacy.
One of Bayes' theorem's many applications is Bayesian inference, an approach to statistical inference, where it is used to invert the probability of observations given a model configuration (i.e., the likelihood function) to obtain the probability of the model configuration given the observations (i.e., the posterior probability).
History
Bayes' theorem is named after Thomas Bayes (/beɪz/), a minister, statistician, and philosopher. Bayes used conditional probability to provide an algorithm (his Proposition 9) that uses evidence to calculate limits on an unknown parameter. His work was published in 1763 as An Essay Towards Solving a Problem in the Doctrine of Chances. Bayes studied how to compute a distribution for the probability parameter of a binomial distribution (in modern terminology). After Bayes's death, his family gave his papers to a friend, the minister, philosopher, and mathematician Richard Price.
Price significantly edited the unpublished manuscript for two years before sending it to a friend who read it aloud at the Royal Society on 23 December 1763. Price edited Bayes's major work "An Essay Towards Solving a Problem in the Doctrine of Chances" (1763), which appeared in Philosophical Transactions, and contains Bayes' theorem. Price wrote an introduction to the paper that provides some of the philosophical basis of Bayesian statistics and chose one of the two solutions Bayes offered. In 1765, Price was elected a Fellow of the Royal Society in recognition of his work on Bayes's legacy. On 27 April, a letter sent to his friend Benjamin Franklin was read out at the Royal Society, and later published, in which Price applies this work to population and computing 'life-annuities'.
Independently of Bayes, Pierre-Simon Laplace used conditional probability to formulate the relation of an updated posterior probability from a prior probability, given evidence. He reproduced and extended Bayes's results in 1774, apparently unaware of Bayes's work, in 1774, and summarized his results in Théorie analytique des probabilités (1812). The Bayesian interpretation of probability was developed mainly by Laplace.
About 200 years later, Sir Harold Jeffreys put Bayes's algorithm and Laplace's formulation on an axiomatic basis, writing in a 1973 book that Bayes' theorem "is to the theory of probability what the Pythagorean theorem is to geometry".
Stephen Stigler used a Bayesian argument to conclude that Bayes' theorem was discovered by Nicholas Saunderson, a blind English mathematician, some time before Bayes, but that is disputed. Martyn Hooper and Sharon McGrayne have argued that Richard Price's contribution was substantial:
By modern standards, we should refer to the Bayes–Price rule. Price discovered Bayes's work, recognized its importance, corrected it, contributed to the article, and found a use for it. The modern convention of employing Bayes's name alone is unfair but so entrenched that anything else makes little sense.
Statement of theorem
Bayes' theorem is stated mathematically as the following equation:
where and are events and .
- is a conditional probability: the probability of event occurring given that is true. It is also called the posterior probability of given .
- is also a conditional probability: the probability of event occurring given that is true. It can also be interpreted as the likelihood of given a fixed because .
- and are the probabilities of observing and respectively without any given conditions; they are known as the prior probability and marginal probability.
Proof

For events
Bayes' theorem may be derived from the definition of conditional probability:
where is the probability of both A and B being true. Similarly,
Solving for and substituting into the above expression for yields Bayes' theorem:
For continuous random variables
For two continuous random variables X and Y, Bayes' theorem may be analogously derived from the definition of conditional density:
Therefore,
General case
Let be the conditional distribution of given and let be the distribution of . The joint distribution is then . The conditional distribution of given is then determined by
Existence and uniqueness of the needed conditional expectation is a consequence of the Radon–Nikodym theorem. This was formulated by Kolmogorov in 1933. Kolmogorov underlines the importance of conditional probability, writing, "I wish to call attention to ... the theory of conditional probabilities and conditional expectations". Bayes' theorem determines the posterior distribution from the prior distribution. Uniqueness requires continuity assumptions. Bayes' theorem can be generalized to include improper prior distributions such as the uniform distribution on the real line. Modern Markov chain Monte Carlo methods have boosted the importance of Bayes' theorem, including in cases with improper priors.
Examples
Recreational mathematics
Bayes' rule and computing conditional probabilities provide a method to solve a number of popular puzzles, such as the Three Prisoners problem, the Monty Hall problem, the Two Child problem, and the Two Envelopes problem.
Drug testing
Suppose, a particular test for whether someone has been using cannabis is 90% sensitive, meaning the true positive rate (TPR) = 0.90. Therefore, it leads to 90% true positive results (correct identification of drug use) for cannabis users.
The test is also 80% specific, meaning true negative rate (TNR) = 0.80. Therefore, the test correctly identifies 80% of non-use for non-users, but also generates 20% false positives, or false positive rate (FPR) = 0.20, for non-users.
Assuming 0.05 prevalence, meaning 5% of people use cannabis, what is the probability that a random person who tests positive is really a cannabis user?
The Positive predictive value (PPV) of a test is the proportion of persons who are actually positive out of all those testing positive, and can be calculated from a sample as:
- PPV = True positive / Tested positive
If sensitivity, specificity, and prevalence are known, PPV can be calculated using Bayes' theorem. Let mean "the probability that someone is a cannabis user given that they test positive", which is what PPV means. We can write:
The denominator is a direct application of the Law of Total Probability. In this case, it says that the probability that someone tests positive is the probability that a user tests positive times the probability of being a user, plus the probability that a non-user tests positive, times the probability of being a non-user. This is true because the classifications user and non-user form a partition of a set, namely the set of people who take the drug test. This combined with the definition of conditional probability results in the above statement.
In other words, if someone tests positive, the probability that they are a cannabis user is only 19%—because in this group, only 5% of people are users, and most positives are false positives coming from the remaining 95%.

If 1,000 people were tested:
- 950 are non-users and 190 of them give false positive (0.20 × 950)
- 50 of them are users and 45 of them give true positive (0.90 × 50)
The 1,000 people thus have 235 positive tests, of which only 45 are genuine, about 19%.
Sensitivity or specificity
The importance of specificity can be seen by showing that even if sensitivity is raised to 100% and specificity remains at 80%, the probability that someone who tests positive is a cannabis user rises only from 19% to 21%, but if the sensitivity is held at 90% and the specificity is increased to 95%, the probability rises to 49%.
| TestActual | Positive | Negative | Total | |
|---|---|---|---|---|
| User | 45 | 5 | 50 | |
| Non-user | 190 | 760 | 950 | |
| Total | 235 | 765 | 1000 | |
| 90% sensitive, 80% specific, PPV=45/235 ≈ 19% | ||||
| TestActual | Positive | Negative | Total | |
|---|---|---|---|---|
| User | 50 | 0 | 50 | |
| Non-user | 190 | 760 | 950 | |
| Total | 240 | 760 | 1000 | |
| 100% sensitive, 80% specific, PPV=50/240 ≈ 21% | ||||
| TestActual | Positive | Negative | Total | |
|---|---|---|---|---|
| User | 45 | 5 | 50 | |
| Non-user | 47 | 903 | 950 | |
| Total | 92 | 908 | 1000 | |
| 90% sensitive, 95% specific, PPV=45/92 ≈ 49% | ||||
Cancer rate
If all patients with pancreatic cancer have a certain symptom, it does not follow that anyone who has that symptom has a 100% chance of getting pancreatic cancer. Assuming the incidence rate of pancreatic cancer is 1/100000, while 10/99999 healthy individuals have the same symptoms worldwide, the probability of having pancreatic cancer given the symptoms is 9.1%, and the other 90.9% could be "false positives" (that is, falsely said to have cancer; "positive" is a confusing term when, as here, the test gives bad news).
Based on incidence rate, the following table presents the corresponding numbers per 100,000 people.
| SymptomCancer | Yes | No | Total | |
|---|---|---|---|---|
| Yes | 1 | 0 | 1 | |
| No | 10 | 99989 | 99999 | |
| Total | 11 | 99989 | 100000 | |
Which can then be used to calculate the probability of having cancer when you have the symptoms:
Defective item rate
| Condition Machine |
Defective | Flawless | Total | |
|---|---|---|---|---|
| A | 10 | 190 | 200 | |
| B | 9 | 291 | 300 | |
| C | 5 | 495 | 500 | |
| Total | 24 | 976 | 1000 | |
A factory produces items using three machines—A, B, and C—which account for 20%, 30%, and 50% of its output, respectively. Of the items produced by machine A, 5% are defective, while 3% of B's items and 1% of C's are defective. If a randomly selected item is defective, what is the probability it was produced by machine C?
Once again, the answer can be reached without using the formula by applying the conditions to a hypothetical number of cases. For example, if the factory produces 1,000 items, 200 will be produced by A, 300 by B, and 500 by C. Machine A will produce 5% × 200 = 10 defective items, B 3% × 300 = 9, and C 1% × 500 = 5, for a total of 24. Thus 24/1000 (2.4%) of the total output will be defective and the likelihood that a randomly selected defective item was produced by machine C is 5/24 (~20.83%).
This problem can also be solved using Bayes' theorem: Let Xi denote the event that a randomly chosen item was made by the i machine (for i = A,B,C). Let Y denote the event that a randomly chosen item is defective. Then, we are given the following information:
If the item was made by the first machine, then the probability that it is defective is 0.05; that is, P(Y | XA) = 0.05. Overall, we have
To answer the original question, we first find P(Y). That can be done in the following way:
Hence, 2.4% of the total output is defective.
We are given that Y has occurred and we want to calculate the conditional probability of XC. By Bayes' theorem,
Given that the item is defective, the probability that it was made by machine C is 5/24. C produces half of the total output but a much smaller fraction of the defective items. Hence the knowledge that the item selected was defective enables us to replace the prior probability P(XC) = 1/2 by the smaller posterior probability P(XC | Y) = 5/24.
Interpretations
The interpretation of Bayes' rule depends on the interpretation of probability ascribed to the terms. The two predominant interpretations are described below.
Bayesian interpretation
In the Bayesian (or epistemological) interpretation, probability measures a "degree of belief". Bayes' theorem links the degree of belief in a proposition before and after accounting for evidence. For example, suppose it is believed with 50% certainty that a coin is twice as likely to land heads than tails. If the coin is flipped a number of times and the outcomes observed, that degree of belief will probably rise or fall, but might remain the same, depending on the results. For proposition A and evidence B,
- P (A), the prior, is the initial degree of belief in A.
- P (A | B), the posterior, is the degree of belief after incorporating news that B is true.
- the quotient P(B | A)/P(B) represents the support B provides for A.
For more on the application of Bayes' theorem under the Bayesian interpretation of probability, see Bayesian inference.
Frequentist interpretation
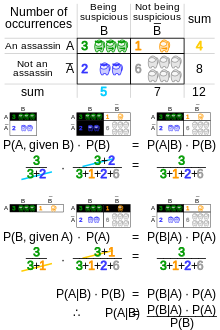
In the frequentist interpretation, probability measures a "proportion of outcomes". For example, suppose an experiment is performed many times. P(A) is the proportion of outcomes with property A (the prior) and P(B) is the proportion with property B. P(B | A) is the proportion of outcomes with property B out of outcomes with property A, and P(A | B) is the proportion of those with A out of those with B (the posterior).
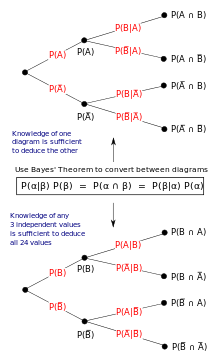
The role of Bayes' theorem can be shown with tree diagrams. The two diagrams partition the same outcomes by A and B in opposite orders, to obtain the inverse probabilities. Bayes' theorem links the different partitionings.
Example
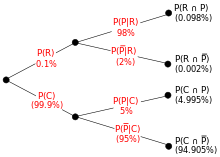
An entomologist spots what might, due to the pattern on its back, be a rare subspecies of beetle. A full 98% of the members of the rare subspecies have the pattern, so P(Pattern | Rare) = 98%. Only 5% of members of the common subspecies have the pattern. The rare subspecies is 0.1% of the total population. How likely is the beetle having the pattern to be rare: what is P(Rare | Pattern)?
From the extended form of Bayes' theorem (since any beetle is either rare or common),
Forms
Events
Simple form
For events A and B, provided that P(B) ≠ 0,
In many applications, for instance in Bayesian inference, the event B is fixed in the discussion and we wish to consider the effect of its having been observed on our belief in various possible events A. In such situations the denominator of the last expression, the probability of the given evidence B, is fixed; what we want to vary is A. Bayes' theorem shows that the posterior probabilities are proportional to the numerator, so the last equation becomes:
In words, the posterior is proportional to the prior times the likelihood.
If events A1, A2, ..., are mutually exclusive and exhaustive, i.e., one of them is certain to occur but no two can occur together, we can determine the proportionality constant by using the fact that their probabilities must add up to one. For instance, for a given event A, the event A itself and its complement ¬A are exclusive and exhaustive. Denoting the constant of proportionality by c, we have:
Adding these two formulas we deduce that:
or
Alternative form
| Background Proposition |
B | ¬B (not B) |
Total | |
|---|---|---|---|---|
| A | P(B|A)⋅P(A) = P(A|B)⋅P(B) |
P(¬B|A)⋅P(A) = P(A|¬B)⋅P(¬B) |
P(A) | |
| ¬A (not A) |
P(B|¬A)⋅P(¬A) = P(¬A|B)⋅P(B) |
P(¬B|¬A)⋅P(¬A) = P(¬A|¬B)⋅P(¬B) |
P(¬A) = 1−P(A) | |
| Total | P(B) | P(¬B) = 1−P(B) | 1 | |
Another form of Bayes' theorem for two competing statements or hypotheses is:
For an epistemological interpretation:
For proposition A and evidence or background B,
- is the prior probability, the initial degree of belief in A.
- is the corresponding initial degree of belief in not-A, that A is false, where
- is the conditional probability or likelihood, the degree of belief in B given that A is true.
- is the conditional probability or likelihood, the degree of belief in B given that A is false.
- is the posterior probability, the probability of A after taking into account B.
Extended form
Often, for some partition {Aj} of the sample space, the event space is given in terms of P(Aj) and P(B | Aj). It is then useful to compute P(B) using the law of total probability:
Or (using the multiplication rule for conditional probability),
In the special case where A is a binary variable:
Random variables
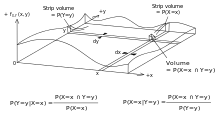
Consider a sample space Ω generated by two random variables X and Y with known probability distributions. In principle, Bayes' theorem applies to the events A = {X = x} and B = {Y = y}.
Terms become 0 at points where either variable has finite probability density. To remain useful, Bayes' theorem can be formulated in terms of the relevant densities (see Derivation).
Simple form
If X is continuous and Y is discrete,
where each is a density function.
If X is discrete and Y is continuous,
If both X and Y are continuous,
Extended form
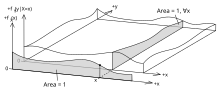
A continuous event space is often conceptualized in terms of the numerator terms. It is then useful to eliminate the denominator using the law of total probability. For fY(y), this becomes an integral:
Bayes' rule in odds form
Bayes' theorem in odds form is:
where
is called the Bayes factor or likelihood ratio. The odds between two events is simply the ratio of the probabilities of the two events. Thus:
Thus the rule says that the posterior odds are the prior odds times the Bayes factor; in other words, the posterior is proportional to the prior times the likelihood.
In the special case that and , one writes , and uses a similar abbreviation for the Bayes factor and for the conditional odds. The odds on is by definition the odds for and against . Bayes' rule can then be written in the abbreviated form
or, in words, the posterior odds on equals the prior odds on times the likelihood ratio for given information . In short, posterior odds equals prior odds times likelihood ratio.
For example, if a medical test has a sensitivity of 90% and a specificity of 91%, then the positive Bayes factor is . Now, if the prevalence of this disease is 9.09%, and if we take that as the prior probability, then the prior odds is about 1:10. So after receiving a positive test result, the posterior odds of having the disease becomes 1:1, which means that the posterior probability of having the disease is 50%. If a second test is performed in serial testing, and that also turns out to be positive, then the posterior odds of having the disease becomes 10:1, which means a posterior probability of about 90.91%. The negative Bayes factor can be calculated to be 91%/(100%-90%)=9.1, so if the second test turns out to be negative, then the posterior odds of having the disease is 1:9.1, which means a posterior probability of about 9.9%.
The example above can also be understood with more solid numbers: assume the patient taking the test is from a group of 1,000 people, 91 of whom have the disease (prevalence of 9.1%). If all 1,000 take the test, 82 of those with the disease will get a true positive result (sensitivity of 90.1%), 9 of those with the disease will get a false negative result (false negative rate of 9.9%), 827 of those without the disease will get a true negative result (specificity of 91.0%), and 82 of those without the disease will get a false positive result (false positive rate of 9.0%). Before taking any test, the patient's odds for having the disease is 91:909. After receiving a positive result, the patient's odds for having the disease is
which is consistent with the fact that there are 82 true positives and 82 false positives in the group of 1,000.
Correspondence to other mathematical frameworks
Propositional logic
Where the conditional probability is defined, it can be seen to capture the implication . The probabilistic calculus then mirrors or even generalizes various logical inference rules. Beyond, for example, assigning binary truth values, here one assigns probability values to statements. The assertion is captured by the assertion , i.e. that the conditional probability take the extremal probability value . Likewise, the assertion of a negation of an implication is captured by the assignment of . So, for example, if , then (if it is defined) , which entails , the implication introduction in logic.
Similarly, as the product of two probabilities equaling necessitates that both factors are also , one finds that Bayes' theorem
entails , which now also includes modus ponens.
For positive values , if it equals , then the two conditional probabilities are equal as well, and vice versa. Note that this mirrors the generally valid .
On the other hand, reasoning about either of the probabilities equalling classically entails the following contrapositive form of the above: .
Bayes' theorem with negated gives
- .
Ruling out the extremal case (i.e. ), one has and in particular
- .
Ruling out also the extremal case , one finds they attain the maximum simultaneously:
which (at least when having ruled out explosive antecedents) captures the classical contraposition principle
- .
Subjective logic
Bayes' theorem represents a special case of deriving inverted conditional opinions in subjective logic expressed as:
where denotes the operator for inverting conditional opinions. The argument denotes a pair of binomial conditional opinions given by source , and the argument denotes the prior probability (aka. the base rate) of . The pair of derivative inverted conditional opinions is denoted . The conditional opinion generalizes the probabilistic conditional , i.e. in addition to assigning a probability the source can assign any subjective opinion to the conditional statement . A binomial subjective opinion is the belief in the truth of statement with degrees of epistemic uncertainty, as expressed by source . Every subjective opinion has a corresponding projected probability . The application of Bayes' theorem to projected probabilities of opinions is a homomorphism, meaning that Bayes' theorem can be expressed in terms of projected probabilities of opinions:
Hence, the subjective Bayes' theorem represents a generalization of Bayes' theorem.
Generalizations
Bayes theorem for 3 events
A version of Bayes' theorem for 3 events results from the addition of a third event , with on which all probabilities are conditioned:
Derivation
Using the chain rule
And, on the other hand
The desired result is obtained by identifying both expressions and solving for .
Use in genetics
In genetics, Bayes' rule can be used to estimate the probability that someone has a specific genotype. Many people seek to assess their chances of being affected by a genetic disease or their likelihood of being a carrier for a recessive gene of interest. A Bayesian analysis can be done based on family history or genetic testing to predict whether someone will develop a disease or pass one on to their children. Genetic testing and prediction is common among couples who plan to have children but are concerned that they may both be carriers for a disease, especially in communities with low genetic variance.
Using pedigree to calculate probabilities
| Hypothesis | Hypothesis 1: Patient is a carrier | Hypothesis 2: Patient is not a carrier |
|---|---|---|
| Prior Probability | 1/2 | 1/2 |
| Conditional Probability that all four offspring will be unaffected | (1/2) ⋅ (1/2) ⋅ (1/2) ⋅ (1/2) = 1/16 | About 1 |
| Joint Probability | (1/2) ⋅ (1/16) = 1/32 | (1/2) ⋅ 1 = 1/2 |
| Posterior Probability | (1/32) / (1/32 + 1/2) = 1/17 | (1/2) / (1/32 + 1/2) = 16/17 |
Example of a Bayesian analysis table for a female's risk for a disease based on the knowledge that the disease is present in her siblings but not in her parents or any of her four children. Based solely on the status of the subject's siblings and parents, she is equally likely to be a carrier as to be a non-carrier (this likelihood is denoted by the Prior Hypothesis). The probability that the subject's four sons would all be unaffected is 1/16 (1⁄2⋅1⁄2⋅1⁄2⋅1⁄2) if she is a carrier and about 1 if she is a non-carrier (this is the Conditional Probability). The Joint Probability reconciles these two predictions by multiplying them together. The last line (the Posterior Probability) is calculated by dividing the Joint Probability for each hypothesis by the sum of both joint probabilities.
Using genetic test results
Parental genetic testing can detect around 90% of known disease alleles in parents that can lead to carrier or affected status in their children. Cystic fibrosis is a heritable disease caused by an autosomal recessive mutation on the CFTR gene, located on the q arm of chromosome 7.
Here is a Bayesian analysis of a female patient with a family history of cystic fibrosis (CF) who has tested negative for CF, demonstrating how the method was used to determine her risk of having a child born with CF: because the patient is unaffected, she is either homozygous for the wild-type allele, or heterozygous. To establish prior probabilities, a Punnett square is used, based on the knowledge that neither parent was affected by the disease but both could have been carriers:
| Mother Father |
W
Homozygous for the wild- |
M
Heterozygous |
|---|---|---|
| W
Homozygous for the wild- |
WW | MW |
| M
Heterozygous (a CF carrier) |
MW | MM
(affected by cystic fibrosis) |
Given that the patient is unaffected, there are only three possibilities. Within these three, there are two scenarios in which the patient carries the mutant allele. Thus the prior probabilities are 2⁄3 and 1⁄3.
Next, the patient undergoes genetic testing and tests negative for cystic fibrosis. This test has a 90% detection rate, so the conditional probabilities of a negative test are 1/10 and 1. Finally, the joint and posterior probabilities are calculated as before.
| Hypothesis | Hypothesis 1: Patient is a carrier | Hypothesis 2: Patient is not a carrier |
|---|---|---|
| Prior Probability | 2/3 | 1/3 |
| Conditional Probability of a negative test | 1/10 | 1 |
| Joint Probability | 1/15 | 1/3 |
| Posterior Probability | 1/6 | 5/6 |
After carrying out the same analysis on the patient's male partner (with a negative test result), the chance that their child is affected is the product of the parents' respective posterior probabilities for being carriers times the chance that two carriers will produce an affected offspring (1⁄4).
Genetic testing done in parallel with other risk factor identification
Bayesian analysis can be done using phenotypic information associated with a genetic condition. When combined with genetic testing, this analysis becomes much more complicated. Cystic fibrosis, for example, can be identified in a fetus with an ultrasound looking for an echogenic bowel, one that appears brighter than normal on a scan. This is not a foolproof test, as an echogenic bowel can be present in a perfectly healthy fetus. Parental genetic testing is very influential in this case, where a phenotypic facet can be overly influential in probability calculation. In the case of a fetus with an echogenic bowel, with a mother who has been tested and is known to be a CF carrier, the posterior probability that the fetus has the disease is very high (0.64). But once the father has tested negative for CF, the posterior probability drops significantly (to 0.16).
Risk factor calculation is a powerful tool in genetic counseling and reproductive planning but cannot be treated as the only important factor. As above, incomplete testing can yield falsely high probability of carrier status, and testing can be financially inaccessible or unfeasible when a parent is not present.
See also
- Bayesian epistemology
- Inductive probability
- Quantum Bayesianism
- Why Most Published Research Findings Are False, a 2005 essay in metascience by John Ioannidis
- Regular conditional probability
- Bayesian persuasion
Notes
- Laplace refined Bayes's theorem over a period of decades:
- Laplace announced his independent discovery of Bayes' theorem in: Laplace (1774) "Mémoire sur la probabilité des causes par les événements", "Mémoires de l'Académie royale des Sciences de MI (Savants étrangers)", 4: 621–656. Reprinted in: Laplace, "Oeuvres complètes" (Paris, France: Gauthier-Villars et fils, 1841), vol. 8, pp. 27–65. Available on-line at: Gallica. Bayes' theorem appears on p. 29.
- Laplace presented a refinement of Bayes' theorem in: Laplace (read: 1783 / published: 1785) "Mémoire sur les approximations des formules qui sont fonctions de très grands nombres", "Mémoires de l'Académie royale des Sciences de Paris", 423–467. Reprinted in: Laplace, "Oeuvres complètes" (Paris, France: Gauthier-Villars et fils, 1844), vol. 10, pp. 295–338. Available on-line at: Gallica. Bayes' theorem is stated on page 301.
- See also: Laplace, "Essai philosophique sur les probabilités" (Paris, France: Mme. Ve. Courcier , 1814), page 10. English translation: Pierre Simon, Marquis de Laplace with F. W. Truscott and F. L. Emory, trans., "A Philosophical Essay on Probabilities" (New York, New York: John Wiley & Sons, 1902), p. 15.
References
- ^ Audun Jøsang, 2016, Subjective Logic; A formalism for Reasoning Under Uncertainty. Springer, Cham, ISBN 978-3-319-42337-1
- Frame, Paul (2015). Liberty's Apostle. Wales: University of Wales Press. p. 44. ISBN 978-1783162161. Retrieved 23 February 2021.
- Allen, Richard (1999). David Hartley on Human Nature. SUNY Press. pp. 243–244. ISBN 978-0791494516. Retrieved 16 June 2013.
- Bayes, Thomas & Price, Richard (1763). "An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S." Philosophical Transactions of the Royal Society of London. 53: 370–418. doi:10.1098/rstl.1763.0053.
- Holland, pp. 46–7.
- Price, Richard (1991). Price: Political Writings. Cambridge University Press. p. xxiii. ISBN 978-0521409698. Retrieved 16 June 2013.
- Mitchell 1911, p. 314.
- Daston, Lorraine (1988). Classical Probability in the Enlightenment. Princeton Univ Press. p. 268. ISBN 0691084971.
- Stigler, Stephen M. (1986). "Inverse Probability". The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 99–138. ISBN 978-0674403413.
- Jeffreys, Harold (1973). Scientific Inference (3rd ed.). Cambridge University Press. p. 31. ISBN 978-0521180788.
- Stigler, Stephen M. (1983). "Who Discovered Bayes' Theorem?". The American Statistician. 37 (4): 290–296. doi:10.1080/00031305.1983.10483122.
- de Vaux, Richard; Velleman, Paul; Bock, David (2016). Stats, Data and Models (4th ed.). Pearson. pp. 380–381. ISBN 978-0321986498.
- Edwards, A. W. F. (1986). "Is the Reference in Hartley (1749) to Bayesian Inference?". The American Statistician. 40 (2): 109–110. doi:10.1080/00031305.1986.10475370.
- Hooper, Martyn (2013). "Richard Price, Bayes' theorem, and God". Significance. 10 (1): 36–39. doi:10.1111/j.1740-9713.2013.00638.x. S2CID 153704746.
- ^ McGrayne, S. B. (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. Yale University Press. ISBN 978-0300188226.
- Stuart, A.; Ord, K. (1994), Kendall's Advanced Theory of Statistics: Volume I – Distribution Theory, Edward Arnold, §8.7
- Kolmogorov, A.N. (1933) . Foundations of the Theory of Probability. Chelsea Publishing Company.
- Tjur, Tue (1980). Probability based on Radon measures. New York: Wiley. ISBN 978-0-471-27824-5.
- Taraldsen, Gunnar; Tufto, Jarle; Lindqvist, Bo H. (2021-07-24). "Improper priors and improper posteriors". Scandinavian Journal of Statistics. 49 (3): 969–991. doi:10.1111/sjos.12550. hdl:11250/2984409. ISSN 0303-6898. S2CID 237736986.
- Robert, Christian P.; Casella, George (2004). Monte Carlo Statistical Methods. Springer. ISBN 978-1475741452. OCLC 1159112760.
- Lee, Peter M. (2012). "Chapter 1". Bayesian Statistics. Wiley. ISBN 978-1-1183-3257-3.
- "Bayes' Theorem: Introduction". Trinity University. Archived from the original on 21 August 2004. Retrieved 5 August 2014.
- "Bayes Theorem - Formula, Statement, Proof | Bayes Rule". Cuemath. Retrieved 2023-10-20.
- Audun Jøsang, 2016, Generalising Bayes' Theorem in Subjective Logic. IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI 2016), Baden-Baden, September 2016
- Koller, D.; Friedman, N. (2009). Probabilistic Graphical Models. Massachusetts: MIT Press. p. 1208. ISBN 978-0-262-01319-2. Archived from the original on 2014-04-27.
- Kraft, Stephanie A; Duenas, Devan; Wilfond, Benjamin S; Goddard, Katrina AB (24 September 2018). "The evolving landscape of expanded carrier screening: challenges and opportunities". Genetics in Medicine. 21 (4): 790–797. doi:10.1038/s41436-018-0273-4. PMC 6752283. PMID 30245516.
- ^ Ogino, Shuji; Wilson, Robert B; Gold, Bert; Hawley, Pamela; Grody, Wayne W (October 2004). "Bayesian analysis for cystic fibrosis risks in prenatal and carrier screening". Genetics in Medicine. 6 (5): 439–449. doi:10.1097/01.GIM.0000139511.83336.8F. PMID 15371910.
- "Types of CFTR Mutations". Cystic Fibrosis Foundation, www.cff.org/What-is-CF/Genetics/Types-of-CFTR-Mutations/.
- "CFTR Gene – Genetics Home Reference". U.S. National Library of Medicine, National Institutes of Health, ghr.nlm.nih.gov/gene/CFTR#location.
Bibliography
 This article incorporates text from a publication now in the public domain: Mitchell, John Malcolm (1911). "Price, Richard". In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 22 (11th ed.). Cambridge University Press. pp. 314–315.
This article incorporates text from a publication now in the public domain: Mitchell, John Malcolm (1911). "Price, Richard". In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 22 (11th ed.). Cambridge University Press. pp. 314–315.
Further reading
- Bolstad, William M.; Curran, James M. (2017). "Logic, Probability, and Uncertainty". Introduction to Bayesian Statistics (3rd ed.). New York: Wiley. pp. 59–82. ISBN 978-1-118-09156-2.
- Lee, Peter M. (2012). Bayesian Statistics: An Introduction (4th ed.). Wiley. ISBN 978-1-118-33257-3.
- Schmitt, Samuel A. (1969). "Accumulating Evidence". Measuring Uncertainty : An Elementary Introduction to Bayesian Statistics. Reading: Addison-Wesley. pp. 61–99. OCLC 5013.
- Stigler, Stephen M. (August 1986). "Laplace's 1774 Memoir on Inverse Probability". Statistical Science. 1 (3): 359–363. doi:10.1214/ss/1177013620.
External links
- "The Bayesian Trap". Veritasium. April 5, 2017 – via YouTube.

 and
and  are
are  .
.
 is a
is a  is also a conditional probability: the probability of event
is also a conditional probability: the probability of event  .
. and
and  are the probabilities of observing
are the probabilities of observing 
 is the probability of both A and B being true. Similarly,
is the probability of both A and B being true. Similarly,





 be the conditional distribution of
be the conditional distribution of  given
given  and let
and let  be the distribution of
be the distribution of  . The joint distribution is then
. The joint distribution is then  . The conditional distribution
. The conditional distribution  of
of  is then determined by
is then determined by

 mean "the probability that someone is a cannabis user given that they test positive", which is what PPV means. We can write:
mean "the probability that someone is a cannabis user given that they test positive", which is what PPV means. We can write:

 is a direct application of the
is a direct application of the 




 are the events rare, common, pattern and no pattern. Percentages in parentheses are calculated. Three independent values are given, so it is possible to calculate the inverse tree.
are the events rare, common, pattern and no pattern. Percentages in parentheses are calculated. Three independent values are given, so it is possible to calculate the inverse tree.






 is the corresponding initial degree of belief in not-A, that A is false, where
is the corresponding initial degree of belief in not-A, that A is false, where 
 is the
is the  is the
is the  is the
is the 





 is a density function.
is a density function.







 and
and  , one writes
, one writes  , and uses a similar abbreviation for the Bayes factor and for the conditional odds. The odds on
, and uses a similar abbreviation for the Bayes factor and for the conditional odds. The odds on 
 . Now, if the
. Now, if the 
 . The probabilistic calculus then mirrors or even generalizes various logical inference rules. Beyond, for example, assigning binary truth values, here one assigns probability values to statements. The assertion
. The probabilistic calculus then mirrors or even generalizes various logical inference rules. Beyond, for example, assigning binary truth values, here one assigns probability values to statements. The assertion  , i.e. that the conditional probability take the extremal probability value
, i.e. that the conditional probability take the extremal probability value  . Likewise, the assertion of a negation of an implication is captured by the assignment of
. Likewise, the assertion of a negation of an implication is captured by the assignment of  . So, for example, if
. So, for example, if  , then (if it is defined)
, then (if it is defined)  , the
, the 
 , which now also includes
, which now also includes  .
.
 .
.
 .
. (i.e.
(i.e.  and in particular
and in particular
 .
. , one finds they attain the maximum
, one finds they attain the maximum 
 .
.
 denotes the operator for inverting conditional opinions. The argument
denotes the operator for inverting conditional opinions. The argument  denotes a pair of binomial conditional opinions given by source
denotes a pair of binomial conditional opinions given by source  , and the argument
, and the argument  denotes the
denotes the  . The conditional opinion
. The conditional opinion  generalizes the probabilistic conditional
generalizes the probabilistic conditional  . A binomial subjective opinion
. A binomial subjective opinion  is the belief in the truth of statement
is the belief in the truth of statement  . The application of Bayes' theorem to projected probabilities of opinions is a
. The application of Bayes' theorem to projected probabilities of opinions is a 
 , with
, with  on which all probabilities are conditioned:
on which all probabilities are conditioned:



 .
.