| Part of a series on |
| Machine learning and data mining |
|---|
| Paradigms |
Problems
|
|
Supervised learning (classification • regression) |
| Clustering |
| Dimensionality reduction |
| Structured prediction |
| Anomaly detection |
| Artificial neural network |
| Reinforcement learning |
| Learning with humans |
| Model diagnostics |
| Mathematical foundations |
| Journals and conferences |
| Related articles |
In the context of artificial neural networks, the rectifier or ReLU (rectified linear unit) activation function is an activation function defined as the non-negative part of its argument, i.e., the ramp function:
where is the input to a neuron. This is analogous to half-wave rectification in electrical engineering.
ReLU is one of the most popular activation function for artificial neural networks, and finds application in computer vision and speech recognition using deep neural nets and computational neuroscience.
It was first used by Alston Householder in 1941 as a mathematical abstraction of biological neural networks. It was introduced by Kunihiko Fukushima in 1969 in the context of visual feature extraction in hierarchical neural networks. It was later argued that it has strong biological motivations and mathematical justifications. In 2011, ReLU activation enabled training deep supervised neural networks without unsupervised pre-training, compared to the widely used activation functions prior to 2011, e.g., the logistic sigmoid (which is inspired by probability theory; see logistic regression) and its more practical counterpart, the hyperbolic tangent.
Advantages
Advantages of ReLU include:
- Sparse activation: for example, in a randomly initialized network, only about 50% of hidden units are activated (i.e. have a non-zero output).
- Better gradient propagation: fewer vanishing gradient problems compared to sigmoidal activation functions that saturate in both directions.
- Efficiency: only requires comparison and addition.
- Scale-invariant (homogeneous):
- .
Potential problems
Possible downsides can include:
- Non-differentiability at zero (however, it is differentiable anywhere else, and the value of the derivative at zero can be chosen to be 0 or 1 arbitrarily).
- Not zero-centered: ReLU outputs are always non-negative. This can make it harder for the network to learn during backpropagation, because gradient updates tend to push weights in one direction (positive or negative). Batch normalization can help address this.
- ReLU is unbounded.
- Dying ReLU: ReLU neurons can sometimes be pushed into states in which they become inactive for essentially all inputs. In this state, no gradients flow backward through the neuron, and so the neuron becomes stuck in a perpetually inactive state (it "dies"). This is a form of the vanishing gradient problem. In some cases, large numbers of neurons in a network can become stuck in dead states, effectively decreasing the model capacity and potentially even halting the learning process. This problem typically arises when the learning rate is set too high. It may be mitigated by using "leaky" ReLU instead, where a small positive slope is assigned for . However, depending on the task, performance may be reduced.
Variants
Piecewise-linear variants
Leaky ReLU allows a small, positive gradient when the unit is inactive, helping to mitigate the vanishing gradient problem. This gradient is defined by a parameter , typically set to 0.01–0.3.
Parametric ReLU (PReLU) takes this idea further by making a learnable parameter along with the other network parameters.
Note that for , this is equivalent to
and thus has a relation to "maxout" networks.
Concatenated ReLU (CReLU) preserves positive and negative phase information:
Other non-linear variants
Gaussian-error linear unit (GELU)
GELU is a smooth approximation to the rectifier:
where is the cumulative distribution function of the standard normal distribution.
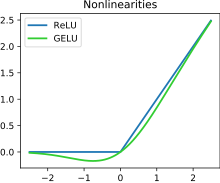
This activation function is illustrated in the figure at the start of this article. It has a "bump" to the left of x < 0 and serves as the default activation for models such as BERT.
SiLU
Main article: Swish functionThe SiLU (sigmoid linear unit) or swish function is another smooth approximation which uses the sigmoid function, first introduced in the GELU paper:
Softplus
Main article: SoftplusA smooth approximation to the rectifier is the analytic function
which is called the softplus or SmoothReLU function. For large negative it is roughly , so just above 0, while for large positive it is roughly , so just above .
This function can be approximated as:
By making the change of variables , this is equivalent to
A sharpness parameter may be included:
The derivative of softplus is the logistic function.
The logistic sigmoid function is a smooth approximation of the derivative of the rectifier, the Heaviside step function.
The multivariable generalization of single-variable softplus is the LogSumExp with the first argument set to zero:
The LogSumExp function is
and its gradient is the softmax; the softmax with the first argument set to zero is the multivariable generalization of the logistic function. Both LogSumExp and softmax are used in machine learning.
ELU
Exponential linear units try to make the mean activations closer to zero, which speeds up learning. It has been shown that ELUs can obtain higher classification accuracy than ReLUs.
In these formulas, is a hyperparameter to be tuned with the constraint .
Given the same interpretation of , ELU can be viewed as a smoothed version of a shifted ReLU (SReLU), which has the form .
Mish
The mish function can also be used as a smooth approximation of the rectifier. It is defined as
where is the hyperbolic tangent, and is the softplus function.
Mish is non-monotonic and self-gated. It was inspired by Swish, itself a variant of ReLU.
Squareplus
Squareplus is the function
where is a hyperparameter that determines the "size" of the curved region near . (For example, letting yields ReLU, and letting yields the metallic mean function.) Squareplus shares many properties with softplus: It is monotonic, strictly positive, approaches 0 as , approaches the identity as , and is smooth. However, squareplus can be computed using only algebraic functions, making it well-suited for settings where computational resources or instruction sets are limited. Additionally, squareplus requires no special consideration to ensure numerical stability when is large.
See also
References
- Brownlee, Jason (8 January 2019). "A Gentle Introduction to the Rectified Linear Unit (ReLU)". Machine Learning Mastery. Retrieved 8 April 2021.
- Liu, Danqing (30 November 2017). "A Practical Guide to ReLU". Medium. Retrieved 8 April 2021.
- Ramachandran, Prajit; Barret, Zoph; Quoc, V. Le (October 16, 2017). "Searching for Activation Functions". arXiv:1710.05941 .
- ^ Xavier Glorot; Antoine Bordes; Yoshua Bengio (2011). Deep sparse rectifier neural networks (PDF). AISTATS.
Rectifier and softplus activation functions. The second one is a smooth version of the first.
- László Tóth (2013). Phone Recognition with Deep Sparse Rectifier Neural Networks (PDF). ICASSP.
- ^ Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models.
- Hansel, D.; van Vreeswijk, C. (2002). "How noise contributes to contrast invariance of orientation tuning in cat visual cortex". J. Neurosci. 22 (12): 5118–5128. doi:10.1523/JNEUROSCI.22-12-05118.2002. PMC 6757721. PMID 12077207.
- Kadmon, Jonathan; Sompolinsky, Haim (2015-11-19). "Transition to Chaos in Random Neuronal Networks". Physical Review X. 5 (4): 041030. arXiv:1508.06486. Bibcode:2015PhRvX...5d1030K. doi:10.1103/PhysRevX.5.041030. S2CID 7813832.
- Engelken, Rainer; Wolf, Fred; Abbott, L. F. (2020-06-03). "Lyapunov spectra of chaotic recurrent neural networks". arXiv:2006.02427 .
- Householder, Alston S. (June 1941). "A theory of steady-state activity in nerve-fiber networks: I. Definitions and preliminary lemmas". The Bulletin of Mathematical Biophysics. 3 (2): 63–69. doi:10.1007/BF02478220. ISSN 0007-4985.
- Fukushima, K. (1969). "Visual feature extraction by a multilayered network of analog threshold elements". IEEE Transactions on Systems Science and Cybernetics. 5 (4): 322–333. doi:10.1109/TSSC.1969.300225.
- Fukushima, K.; Miyake, S. (1982). "Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Visual Pattern Recognition". Competition and Cooperation in Neural Nets. Lecture Notes in Biomathematics. Vol. 45. Springer. pp. 267–285. doi:10.1007/978-3-642-46466-9_18. ISBN 978-3-540-11574-8.
{{cite book}}:|journal=ignored (help) - Hahnloser, R.; Sarpeshkar, R.; Mahowald, M. A.; Douglas, R. J.; Seung, H. S. (2000). "Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit". Nature. 405 (6789): 947–951. Bibcode:2000Natur.405..947H. doi:10.1038/35016072. PMID 10879535. S2CID 4399014.
- Hahnloser, R.; Seung, H. S. (2001). Permitted and Forbidden Sets in Symmetric Threshold-Linear Networks. NIPS 2001.
- Yann LeCun; Leon Bottou; Genevieve B. Orr; Klaus-Robert Müller (1998). "Efficient BackProp" (PDF). In G. Orr; K. Müller (eds.). Neural Networks: Tricks of the Trade. Springer.
- "PyTorch Leaky ReLU docs".
- "TensorFlow Leaky ReLU docs".
- ^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on Image Net Classification". arXiv:1502.01852 .
- Shang, Wenling; Sohn, Kihyuk; Almeida, Diogo; Lee, Honglak (2016-06-11). "Understanding and Improving Convolutional Neural Networks via Concatenated Rectified Linear Units". Proceedings of the 33rd International Conference on Machine Learning. PMLR: 2217–2225. arXiv:1603.05201.
- ^ Hendrycks, Dan; Gimpel, Kevin (2016). "Gaussian Error Linear Units (GELUs)". arXiv:1606.08415 .
- ^ Diganta Misra (23 Aug 2019), Mish: A Self Regularized Non-Monotonic Activation Function (PDF), arXiv:1908.08681v1, retrieved 26 March 2022.
- Dugas, Charles; Bengio, Yoshua; Bélisle, François; Nadeau, Claude; Garcia, René (2000-01-01). "Incorporating second-order functional knowledge for better option pricing" (PDF). Proceedings of the 13th International Conference on Neural Information Processing Systems (NIPS'00). MIT Press: 451–457.
Since the sigmoid h has a positive first derivative, its primitive, which we call softplus, is convex.
- "Smooth Rectifier Linear Unit (SmoothReLU) Forward Layer". Developer Guide for Intel Data Analytics Acceleration Library. 2017. Retrieved 2018-12-04.
- Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015). "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". arXiv:1511.07289 .
- ^ Shaw, Sweta (2020-05-10). "Activation Functions Compared with Experiments". W&B. Retrieved 2022-07-11.
- Barron, Jonathan T. (22 December 2021). "Squareplus: A Softplus-Like Algebraic Rectifier". arXiv:2112.11687 .

 is the input to a
is the input to a  .
. . However, depending on the task, performance may be reduced.
. However, depending on the task, performance may be reduced. , typically set to 0.01–0.3.
, typically set to 0.01–0.3.

 , this is equivalent to
, this is equivalent to




 is the
is the 


 , so just above 0, while for large positive
, so just above 0, while for large positive  , so just above
, so just above 
 , this is equivalent to
, this is equivalent to

 may be included:
may be included:




 .
.
 .
.

 is the
is the  is the
is the 
 is a hyperparameter that determines the "size" of the curved region near
is a hyperparameter that determines the "size" of the curved region near  . (For example, letting
. (For example, letting  yields ReLU, and letting
yields ReLU, and letting  yields the
yields the  , approaches the identity as
, approaches the identity as  , and is
, and is 