
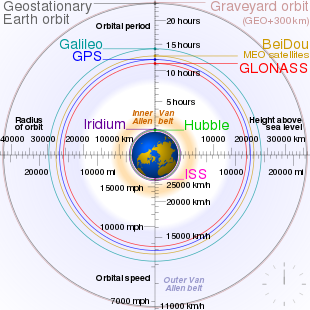
A geostationary orbit, also referred to as a geosynchronous equatorial orbit (GEO), is a circular geosynchronous orbit 35,786 km (22,236 mi) in altitude above Earth's equator, 42,164 km (26,199 mi) in radius from Earth's center, and following the direction of Earth's rotation.
An object in such an orbit has an orbital period equal to Earth's rotational period, one sidereal day, and so to ground observers it appears motionless, in a fixed position in the sky. The concept of a geostationary orbit was popularised by the science fiction writer Arthur C. Clarke in the 1940s as a way to revolutionise telecommunications, and the first satellite to be placed in this kind of orbit was launched in 1963.
Communications satellites are often placed in a geostationary orbit so that Earth-based satellite antennas do not have to rotate to track them but can be pointed permanently at the position in the sky where the satellites are located. Weather satellites are also placed in this orbit for real-time monitoring and data collection, and navigation satellites to provide a known calibration point and enhance GPS accuracy.
Geostationary satellites are launched via a temporary orbit, and then placed in a "slot" above a particular point on the Earth's surface. The satellite requires periodic station-keeping to maintain its position. Modern retired geostationary satellites are placed in a higher graveyard orbit to avoid collisions.
History

In 1929, Herman Potočnik described both geosynchronous orbits in general and the special case of the geostationary Earth orbit in particular as useful orbits for space stations. The first appearance of a geostationary orbit in popular literature was in October 1942, in the first Venus Equilateral story by George O. Smith, but Smith did not go into details. British science fiction author Arthur C. Clarke popularised and expanded the concept in a 1945 paper entitled Extra-Terrestrial Relays – Can Rocket Stations Give Worldwide Radio Coverage?, published in Wireless World magazine. Clarke acknowledged the connection in his introduction to The Complete Venus Equilateral. The orbit, which Clarke first described as useful for broadcast and relay communications satellites, is sometimes called the Clarke orbit. Similarly, the collection of artificial satellites in this orbit is known as the Clarke Belt.
In technical terminology the orbit is referred to as either a geostationary or geosynchronous equatorial orbit, with the terms used somewhat interchangeably.
The first geostationary satellite was designed by Harold Rosen while he was working at Hughes Aircraft in 1959. Inspired by Sputnik 1, he wanted to use a geostationary satellite to globalise communications. Telecommunications between the US and Europe was then possible between just 136 people at a time, and reliant on high frequency radios and an undersea cable.
Conventional wisdom at the time was that it would require too much rocket power to place a satellite in a geostationary orbit and it would not survive long enough to justify the expense, so early efforts were put towards constellations of satellites in low or medium Earth orbit. The first of these were the passive Echo balloon satellites in 1960, followed by Telstar 1 in 1962. Although these projects had difficulties with signal strength and tracking, issues that could be solved using geostationary orbits, the concept was seen as impractical, so Hughes often withheld funds and support.
By 1961, Rosen and his team had produced a cylindrical prototype with a diameter of 76 centimetres (30 in), height of 38 centimetres (15 in), weighing 11.3 kilograms (25 lb), light and small enough to be placed into orbit. It was spin stabilised with a dipole antenna producing a pancake shaped beam. In August 1961, they were contracted to begin building the real satellite. They lost Syncom 1 to electronics failure, but Syncom 2 was successfully placed into a geosynchronous orbit in 1963. Although its inclined orbit still required moving antennas, it was able to relay TV transmissions, and allowed for US President John F. Kennedy in Washington D.C., to phone Nigerian prime minister Abubakar Tafawa Balewa aboard the USNS Kingsport docked in Lagos on August 23, 1963.
The first satellite placed in a geostationary orbit was Syncom 3, which was launched by a Delta D rocket in 1964. With its increased bandwidth, this satellite was able to transmit live coverage of the Summer Olympics from Japan to America. Geostationary orbits have been in common use ever since, in particular for satellite television.
Today there are hundreds of geostationary satellites providing remote sensing and communications.
Although most populated land locations on the planet now have terrestrial communications facilities (microwave, fiber-optic), with telephone access covering 96% of the population and internet access 90%, some rural and remote areas in developed countries are still reliant on satellite communications.
Uses
See also: Geosynchronous satelliteMost commercial communications satellites, broadcast satellites and SBAS satellites operate in geostationary orbits.
Communications
Geostationary communication satellites are useful because they are visible from a large area of the earth's surface, extending 81° away in latitude and 77° in longitude. They appear stationary in the sky, which eliminates the need for ground stations to have movable antennas. This means that Earth-based observers can erect small, cheap and stationary antennas that are always directed at the desired satellite. However, latency becomes significant as it takes about 240 ms for a signal to pass from a ground based transmitter on the equator to the satellite and back again. This delay presents problems for latency-sensitive applications such as voice communication, so geostationary communication satellites are primarily used for unidirectional entertainment and applications where low latency alternatives are not available.
Geostationary satellites are directly overhead at the equator and appear lower in the sky to an observer nearer the poles. As the observer's latitude increases, communication becomes more difficult due to factors such as atmospheric refraction, Earth's thermal emission, line-of-sight obstructions, and signal reflections from the ground or nearby structures. At latitudes above about 81°, geostationary satellites are below the horizon and cannot be seen at all. Because of this, some Russian communication satellites have used elliptical Molniya and Tundra orbits, which have excellent visibility at high latitudes.
Meteorology
See also: Weather satelliteA worldwide network of operational geostationary meteorological satellites is used to provide visible and infrared images of Earth's surface and atmosphere for weather observation, oceanography, and atmospheric tracking. As of 2019 there are 19 satellites in either operation or stand-by. These satellite systems include:
- the United States' GOES series, operated by NOAA
- the Meteosat series, launched by the European Space Agency and operated by the European Weather Satellite Organization, EUMETSAT
- the Republic of Korea COMS-1 and GK-2A multi mission satellites.
- the Russian Elektro-L satellites
- the Japanese Himawari series
- Chinese Fengyun series
- India's INSAT series
These satellites typically capture images in the visual and infrared spectrum with a spatial resolution between 0.5 and 4 square kilometres. The coverage is typically 70°, and in some cases less.
Geostationary satellite imagery has been used for tracking volcanic ash, measuring cloud top temperatures and water vapour, oceanography, measuring land temperature and vegetation coverage, facilitating cyclone path prediction, and providing real time cloud coverage and other tracking data. Some information has been incorporated into meteorological prediction models, but due to their wide field of view, full-time monitoring and lower resolution, geostationary weather satellite images are primarily used for short-term and real-time forecasting.
Navigation
Further information: GNSS augmentation
Geostationary satellites can be used to augment GNSS systems by relaying clock, ephemeris and ionospheric error corrections (calculated from ground stations of a known position) and providing an additional reference signal. This improves position accuracy from approximately 5m to 1m or less.
Past and current navigation systems that use geostationary satellites include:
- The Wide Area Augmentation System (WAAS), operated by the United States Federal Aviation Administration (FAA);
- The European Geostationary Navigation Overlay Service (EGNOS), operated by the ESSP (on behalf of EU's GSA);
- The Multi-functional Satellite Augmentation System (MSAS), operated by Japan's Ministry of Land, Infrastructure and Transport Japan Civil Aviation Bureau (JCAB);
- The GPS Aided Geo Augmented Navigation (GAGAN) system being operated by India.
- The commercial StarFire navigation system, operated by John Deere and C-Nav Positioning Solutions (Oceaneering);
- The commercial Starfix DGPS System and OmniSTAR system, operated by Fugro.
Implementation
Launch
See also: Geostationary transfer orbit
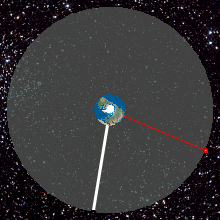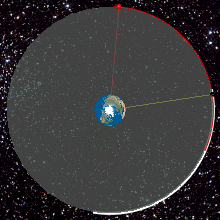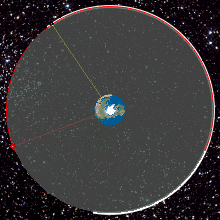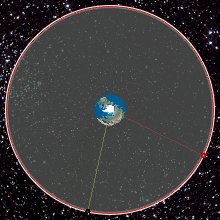
 An example of a transition from temporary GTO to GSO.
An example of a transition from temporary GTO to GSO.EchoStar XVII · Earth.
Geostationary satellites are launched to the east into a prograde orbit that matches the rotation rate of the equator. The smallest inclination that a satellite can be launched into is that of the launch site's latitude, so launching the satellite from close to the equator limits the amount of inclination change needed later. Additionally, launching from close to the equator allows the speed of the Earth's rotation to give the satellite a boost. A launch site should have water or deserts to the east, so any failed rockets do not fall on a populated area.
Most launch vehicles place geostationary satellites directly into a geostationary transfer orbit (GTO), an elliptical orbit with an apogee at GEO height and a low perigee. On-board satellite propulsion is then used to raise the perigee, circularise and reach GEO.
Orbit allocation
See also: Bogota DeclarationSatellites in geostationary orbit must all occupy a single ring above the equator. The requirement to space these satellites apart, to avoid harmful radio-frequency interference during operations, means that there are a limited number of orbital slots available, and thus only a limited number of satellites can be operated in geostationary orbit. This has led to conflict between different countries wishing access to the same orbital slots (countries near the same longitude but differing latitudes) and radio frequencies. These disputes are addressed through the International Telecommunication Union's allocation mechanism under the Radio Regulations. In the 1976 Bogota Declaration, eight countries located on the Earth's equator claimed sovereignty over the geostationary orbits above their territory, but the claims gained no international recognition.
Statite proposal
A statite is a hypothetical satellite that uses radiation pressure from the sun against a solar sail to modify its orbit.
It would hold its location over the dark side of the Earth at a latitude of approximately 30 degrees. A statite is stationary relative to the Earth and Sun system rather than compared to surface of the Earth, and could ease congestion in the geostationary ring.
Retired satellites
Geostationary satellites require some station keeping to keep their position, and once they run out of thruster fuel they are generally retired. The transponders and other onboard systems often outlive the thruster fuel and by allowing the satellite to move naturally into an inclined geosynchronous orbit some satellites can remain in use, or else be elevated to a graveyard orbit. This process is becoming increasingly regulated and satellites must have a 90% chance of moving over 200 km above the geostationary belt at end of life.
Space debris
Main article: Space debris § Characterization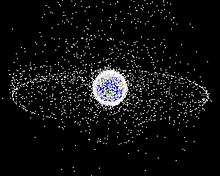
Space debris at geostationary orbits typically has a lower collision speed than at low Earth orbit (LEO) since all GEO satellites orbit in the same plane, altitude and speed; however, the presence of satellites in eccentric orbits allows for collisions at up to 4 km/s. Although a collision is comparatively unlikely, GEO satellites have a limited ability to avoid any debris.
At geosynchronous altitude, objects less than 10 cm in diameter cannot be seen from the Earth, making it difficult to assess their prevalence.
Despite efforts to reduce risk, spacecraft collisions have occurred. The European Space Agency telecom satellite Olympus-1 was struck by a meteoroid on August 11, 1993, and eventually moved to a graveyard orbit, and in 2006 the Russian Express-AM11 communications satellite was struck by an unknown object and rendered inoperable, although its engineers had enough contact time with the satellite to send it into a graveyard orbit. In 2017, both AMC-9 and Telkom-1 broke apart from an unknown cause.
Properties
A typical geostationary orbit has the following properties:
- Inclination: 0°
- Period: 1436 minutes (one sidereal day)
- Eccentricity: 0
- Argument of perigee: undefined
- Semi-major axis: 42,164 km
Inclination
An inclination of zero ensures that the orbit remains over the equator at all times, making it stationary with respect to latitude from the point of view of a ground observer (and in the Earth-centered Earth-fixed reference frame).
Period
The orbital period is equal to exactly one sidereal day. This means that the satellite will return to the same point above the Earth's surface every (sidereal) day, regardless of other orbital properties. For a geostationary orbit in particular, it ensures that it holds the same longitude over time. This orbital period, T, is directly related to the semi-major axis of the orbit through the formula:
where:
- a is the length of the orbit's semi-major axis
- μ is the standard gravitational parameter of the central body
Eccentricity
The eccentricity is zero, which produces a circular orbit. This ensures that the satellite does not move closer or further away from the Earth, which would cause it to track backwards and forwards across the sky.
Stability
A geostationary orbit can be achieved only at an altitude very close to 35,786 kilometres (22,236 miles) and directly above the equator. This equates to an orbital speed of 3.07 kilometres per second (1.91 miles per second) and an orbital period of 1,436 minutes, one sidereal day. This ensures that the satellite will match the Earth's rotational period and has a stationary footprint on the ground. All geostationary satellites have to be located on this ring.
A combination of lunar gravity, solar gravity, and the flattening of the Earth at its poles causes a precession motion of the orbital plane of any geostationary object, with an orbital period of about 53 years and an initial inclination gradient of about 0.85° per year, achieving a maximal inclination of 15° after 26.5 years. To correct for this perturbation, regular orbital stationkeeping maneuvers are necessary, amounting to a delta-v of approximately 50 m/s per year.
A second effect to be taken into account is the longitudinal drift, caused by the asymmetry of the Earth – the equator is slightly elliptical (equatorial eccentricity). There are two stable equilibrium points sometimes called "gravitational wells" (at 75.3°E and 108°W) and two corresponding unstable points (at 165.3°E and 14.7°W). Any geostationary object placed between the equilibrium points would (without any action) be slowly accelerated towards the stable equilibrium position, causing a periodic longitude variation. The correction of this effect requires station-keeping maneuvers with a maximal delta-v of about 2 m/s per year, depending on the desired longitude.
Solar wind and radiation pressure also exert small forces on satellites: over time, these cause them to slowly drift away from their prescribed orbits.
In the absence of servicing missions from the Earth or a renewable propulsion method, the consumption of thruster propellant for station-keeping places a limitation on the lifetime of the satellite. Hall-effect thrusters, which are currently in use, have the potential to prolong the service life of a satellite by providing high-efficiency electric propulsion.
Derivation
For circular orbits around a body, the centripetal force required to maintain the orbit (Fc) is equal to the gravitational force acting on the satellite (Fg):
From Isaac Newton's universal law of gravitation,
- ,
where Fg is the gravitational force acting between two objects, ME is the mass of the Earth, 5.9736×10 kg, ms is the mass of the satellite, r is the distance between the centers of their masses, and G is the gravitational constant, (6.67428±0.00067)×10 m kg s.
The magnitude of the acceleration, a, of a body moving in a circle is given by:
where v is the magnitude of the velocity (i.e. the speed) of the satellite. From Newton's second law of motion, the centripetal force Fc is given by:
- .
As Fc = Fg,
- ,
so that
Replacing v with the equation for the speed of an object moving around a circle produces:
where T is the orbital period (i.e. one sidereal day), and is equal to 86164.09054 s. This gives an equation for r:
The product GME is known with much greater precision than either factor alone; it is known as the geocentric gravitational constant μ = 398600.4418±0.0008 km s. Hence
The resulting orbital radius is 42,164 kilometres (26,199 miles). Subtracting the Earth's equatorial radius, 6,378 kilometres (3,963 miles), gives the altitude of 35,786 kilometres (22,236 miles).
The orbital speed is calculated by multiplying the angular speed by the orbital radius:
In other planets
By the same method, we can determine the orbital altitude for any similar pair of bodies, including the areostationary orbit of an object in relation to Mars, if it is assumed that it is spherical (which it is not entirely). The gravitational constant GM (μ) for Mars has the value of 42830 km s, its equatorial radius is 3389.50 km and the known rotational period (T) of the planet is 1.02595676 Earth days (88642.66 s). Using these values, Mars' orbital altitude is equal to 17039 km.
See also
- List of orbits
- List of satellites in geosynchronous orbit
- Orbital station-keeping
- Space elevator, which ultimately reaches to and beyond a geostationary orbit
Explanatory notes
- Geostationary orbit and Geosynchronous (equatorial) orbit are used somewhat interchangeably in sources.
- Orbital periods and speeds are calculated using the relations 4πR = TGM and VR = GM, where R is the radius of orbit in metres; T, the orbital period in seconds; V, the orbital speed in m/s; G, the gravitational constant ≈ 6.673×10 Nm/kg; M, the mass of Earth ≈ 5.98×10 kg.
- The Moon's orbit is not perfectly circular, and is approximately 8.6 times further away from the Earth than the geostationary ring when the Moon is at perigee (363 104 km ÷ 42 164 km) and 9.6 times further away when the Moon is at apogee (405,696 km ÷ 42,164 km).
References
- Noordung, Hermann (1929). Das Problem der Befahrung des Weltraums: Der Raketen-Motor (PDF). Berlin: Richard Carl Schmidt & Co. pp. 98–100.
- "(Korvus's message is sent) to a small, squat building at the outskirts of Northern Landing. It was hurled at the sky. ... It ... arrived at the relay station tired and worn, ... when it reached a space station only five hundred miles above the city of North Landing." Smith, George O. (1976). The Complete Venus Equilateral. New York: Ballantine Books. pp. 3–4. ISBN 978-0-345-28953-7.
- "It is therefore quite possible that these stories influenced me subconsciously when ... I worked out the principles of synchronous communications satellites ...", McAleer, Neil (1992). Arthur C. Clarke. Contemporary Books. p. 54. ISBN 978-0-809-24324-2.
- ^ Arthur C. Clarke (October 1945). "Extraterrestrial Relays: Can Rocket Stations Give World-wide Radio Coverage?" (PDF). Arthur C. Clarke Institute for Space Education. Archived (PDF) from the original on October 9, 2022. Retrieved January 1, 2021.
- Phillips Davis (ed.). "Basics of Space Flight Section 1 Part 5, Geostationary Orbits". NASA. Archived from the original on December 12, 2012. Retrieved August 25, 2019.
- Mills, Mike (August 3, 1997). "Orbit Wars: Arthur C. Clarke and the Global Communications Satellite". The Washington Post Magazine. pp. 12–13. Retrieved August 25, 2019.
- Kidder, S.Q. (2015). "Satellites and satellite remote senssing: Orbits". In North, Gerald; Pyla, John; Zhang, Fuqing (eds.). Encyclopedia of Atmospheric Sciences (2 ed.). Elsiver. pp. 95–106. doi:10.1016/B978-0-12-382225-3.00362-5. ISBN 9780123822253.
- ^ McClintock, Jack (November 9, 2003). "Communications: Harold Rosen – The Seer of Geostationary Satellites". Discover Magazine. Retrieved August 25, 2019.
- Perkins, Robert (January 31, 2017). Harold Rosen, 1926–2017. Caltech. Retrieved August 25, 2019.
- ^ Vartabedian, Ralph (July 26, 2013). "How a satellite called Syncom changed the world". Los Angeles Times. Retrieved August 25, 2019.
- Daniel R. Glover (1997). "Chapter 6: NASA Experimental Communications Satellites, 1958-1995". In Andrew J Butrica (ed.). Beyond The Ionosphere: Fifty Years of Satellite Communication. NASA. Bibcode:1997bify.book.....B.
- David R. Williams (ed.). "Syncom 2". NASA. Retrieved September 29, 2019.
- "World's First Geosynchronous Satellite Launched". History Channel. Foxtel. June 19, 2016. Archived from the original on December 7, 2019. Retrieved August 25, 2019.
- David R. Williams (ed.). "Syncom 3". NASA. Retrieved September 29, 2019.
- Howell, Elizabeth (April 24, 2015). "What Is a Geosynchronous Orbit?". Space.com. Retrieved August 25, 2019.
- "ITU releases 2018 global and regional ICT estimates". International Telecommunication Union. December 7, 2018. Retrieved August 25, 2019.
- Thompson, Geoff (April 24, 2019). "Australia was promised superfast broadband with the NBN. This is what we got". ABC. Retrieved August 25, 2019.
- Tibken, Shara (October 22, 2018). "In farm country, forget broadband. You might not have internet at all. 5G is around the corner, yet pockets of America still can't get basic internet access". CNET. Retrieved August 25, 2019.
- "Orbits". ESA. October 4, 2018. Retrieved October 1, 2019.
- ^ "Deployment of an SBAS system demonstration in Southern Africa". GMV. August 6, 2016. Retrieved October 1, 2019.
- Richard Thompson. "Satellites, Geo-stationary orbits and Solar Eclipses". BOM. Retrieved October 1, 2019.
- ^ Soler, Tomás; Eisemann, David W. (August 1994). "Determination of Look Angles To Geostationary Communication Satellites" (PDF). Journal of Surveying Engineering. 120 (3): 123. doi:10.1061/(ASCE)0733-9453(1994)120:3(115). ISSN 0733-9453. Archived (PDF) from the original on October 9, 2022. Retrieved April 16, 2019.
- ^ Wertz, James Richard; Larson, Wiley J. (1999). Larson, Wiley J.; Wertz, James R. (eds.). Space Mission Analysis and Design. Microcosm Press and Kluwer Academic Publishers. Bibcode:1999smad.book.....W. ISBN 1-881883-10-8.
- Kohn, Daniel (March 6, 2016). "The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide". Teledesic Corporation, USA.
- Freeman, Roger L. (July 22, 2002). "Satellite Communications". Reference Manual for Telecommunications Engineering. American Cancer Society. doi:10.1002/0471208051.fre018. ISBN 0471208051.
- History Committee of the American Astronautical Society (August 23, 2010). Johnson, Stephen B. (ed.). Space Exploration and Humanity: A Historical Encyclopedia. Vol. 1. Greenwood Publishing Group. p. 416. ISBN 978-1-85109-514-8. Retrieved April 17, 2019.
- "Satellite Status". World Meteorological Organization. Retrieved July 6, 2019.
- "Our Satellites". NOAA National Environmental Satellite, Data, and Information Service (NESDIS).
- "Meteosat". EUMETSAT.int. Archived from the original on January 14, 2020. Retrieved July 1, 2019.
- "Satellite Launches for the Middle East and South Korea" (PDF). Arianespace. Archived from the original (PDF) on July 4, 2010. Retrieved June 26, 2010.
- Heinrich, Ralph (September 9, 2014). "Airbus Defence and Space supports South Korean weather satellite programme". Airbus. Archived from the original on December 26, 2019. Retrieved July 2, 2019.
- Graham, William (October 6, 2014). "Japan lofts Himawari 8 weather satellite via H-IIA rocket". NASASpaceFlight.com.
- "China plans to launch additional nine Fengyun meteorological satellites by 2025". GBTimes. November 15, 2018. Archived from the original on July 2, 2019. Retrieved July 2, 2019.
- ^ "RAPID: Gateway to Indian Weather Satellite Data". Indian Space Research Organisation. July 2, 2019. Archived from the original on December 25, 2019. Retrieved July 2, 2019.
- ^ "About environmental satellites". BOM. Retrieved July 6, 2019.
- "Coverage of a geostationary satellite at Earth". The Planetary Society.
- "NOAA Satellites, Scientists Monitor Mt. St. Helens for Possible Eruption". SpaceRef. October 6, 2004. Archived from the original on September 10, 2012. Retrieved July 1, 2019.
- "GOCI". NASA. Archived from the original on June 24, 2021. Retrieved August 25, 2019.
- Miura, Tomoaki; Nagai, Shin; Takeuchi, Mika; Ichii, Kazuhito; Yoshioka, Hiroki (October 30, 2019). "Improved Characterisation of Vegetation and Land Surface Seasonal Dynamics in Central Japan with Himawari-8 Hypertemporal Data". Scientific Reports. 9 (1): 15692. Bibcode:2019NatSR...915692M. doi:10.1038/s41598-019-52076-x. ISSN 2045-2322. PMC 6821777. PMID 31666582.
- ^ Hanson, Derek; Peronto, James; Hilderbrand, Douglas (November 12, 2015). "NOAA's Eyes in the Sky – After Five Decades of Weather Forecasting with Environmental Satellites, What Do Future Satellites Promise for Meteorologists and Society?". World Meteorological Organization. Archived from the original on December 18, 2023. Retrieved July 2, 2019.
- "GOES-R: Today's Satellite for Tomorrow's Forecast Dataset". Science On a Sphere. NOAA. November 14, 2016.
- Tollefson, Jeff (March 2, 2018). "Latest US weather satellite highlights forecasting challenges". Nature. 555 (7695): 154. Bibcode:2018Natur.555..154T. doi:10.1038/d41586-018-02630-w. PMID 29517031.
- "Satellite Navigation – WAAS – How It Works". FAA. June 12, 2019.
- "Satellite Based Augmentation System test-bed project". Geoscience Australia. Archived from the original on July 7, 2019.
- "GAGAN System Certified for RNP0.1 Operations" (Press release). Indian Space Research Organisation. January 3, 2014. Archived from the original on January 3, 2014.
- Radhakrishnan, S. Anil (January 11, 2014). "GAGAN system ready for operations". The Hindu.
- Ott, L. E. Mattok, C. (ed.). Ten Years of Experience with A Commercial Satellite Navigation System. International Cooperation in Satellite Communications, Proceedings of the AIAA/ESA Workshop. ESTEC, Noordwijk, the Netherlands. p. 101. Bibcode:1995ESASP.372..101O.
- ^ Farber, Nicholas; Aresini, Andrea; Wauthier, Pascal; Francken, Philippe (September 2007). A general approach to the geostationary transfer orbit mission recovery. 20th International Symposium on Space Flight Dynamics. p. 2.
- "Launching Satellites". Eumetsat. Archived from the original on December 21, 2019. Retrieved July 22, 2019.
- Jason Davis (January 17, 2014). "How to get a satellite to geostationary orbit". The Planetary Society. Retrieved October 2, 2019.
- Henri, Yvon. "Orbit/Spectrum Allocation Procedures Registration Mechanism under the Radio Regulations". Space Services Department. Archived from the original on March 27, 2009.
- "Space Services Division". ITU. Retrieved July 26, 2019.
- Oduntan, Gbenga. "The Never Ending Dispute: Legal Theories on the Spatial Demarcation Boundary Plane between Airspace and Outer Space". Hertfordshire Law Journal. 1 (2): 75. S2CID 10047170.
- US patent 5183225, Forward, Robert, "STATITE: SPACECRAFT THAT UTILIZES SIGHT PRESSURE AND METHOD OF USE", published February 2, 1993
- "Science: Polar 'satellite' could revolutionise communications". New Scientist. No. 1759. March 9, 1991. Retrieved October 2, 2019.
- "Inclined orbit operation". SatSig.net.
- EUMETSAT (April 3, 2017). "Where old satellites go to die". phys.org.
- Marric Stephens (December 12, 2017). "Space debris threat to geosynchronous satellites has been drastically underestimated". Physics World.
- ^ Caleb Henry (August 30, 2017). "ExoAnalytic video shows Telkom-1 satellite erupting debris". SpaceNews.com.
- "The Olympus failure" ESA press release, August 26, 1993. Archived September 11, 2007, at the Wayback Machine
- "Notification for Express-AM11 satellite users in connection with the spacecraft failure" Russian Satellite Communications Company, April 19, 2006.
- Dunstan, James E. (January 30, 2018). "Do we care about orbital debris at all?". SpaceNews.com.
- "AMC 9 Satellite Anomaly associated with Energetic Event & sudden Orbit Change – Spaceflight101". spaceflight101.com. June 20, 2017.
- ^ Anderson, Paul; et al. (2015). Operational Considerations of GEO Debris Synchronization Dynamics (PDF). 66th International Astronautical Congress. Jerusalem, Israel. IAC-15,A6,7,3,x27478. Archived (PDF) from the original on October 9, 2022.
- ^ Dundeck, M; Doveil, F; Arcis, N; Zurbach, S (2012). Plasma propulsion for geostationary satellites fortelecommunication and interplanetary missions. IOP Conference Series: Materials Science and Engineering. doi:10.1088/1757-899X/29/1/012010.
- Jefferson Barker (March 2006). U.S. Military Space Reference Text (PDF). National Security Space Institute. p. 56.
- Kelly, Patrick; Erwin, Richard S.; Bevilacqua, Riccardo; Mazal, Leonel (2016). Solar radiation pressure applications on geostationary satellites (PDF). Proceedings of the 2016 AAS GP & C Conference. American Astronautical Society. Archived (PDF) from the original on October 9, 2022.
- ^ Pople, Stephen (2001). Advanced Physics Through Diagrams. Oxford University Press. p. 72. ISBN 0-19-914199-1.
- Edited by P. Kenneth Seidelmann, "Explanatory Supplement to the Astronomical Almanac", University Science Books,1992, p. 700.
- Mohindroo, K. K. (1997). Basic Principles of Physics. Vol. 1. New Delhi: Pitambar Publishing Company. pp. 6–8.19. ISBN 81-209-0199-1.
- Elert, Glenn (2019). "Orbital Mechanics I". The Physics Hypertextbook. Retrieved September 30, 2019.
- Lakdawalla, Emily (2013). "Stationkeeping in Mars orbit". The Planetary Society. Retrieved September 30, 2019.
- "Solar System Dynamics". NASA. 2017. Retrieved September 30, 2019.
![]() This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on January 22, 2022. (in support of MIL-STD-188).
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on January 22, 2022. (in support of MIL-STD-188).
External links
- How to get a satellite to geostationary orbit
- Orbital Mechanics (Rocket and Space Technology)
- List of satellites in geostationary orbit
- Clarke Belt Snapshot Calculator
- 3D Real Time Satellite Tracking
- Geostationary satellite orbit overview
- Daily animation of the Earth, made by geostationary satellite 'Electro L' photos Satellite shoots 48 images of the planet every day.
- Orbital Mechanics for Engineering Students
| Gravitational orbits | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Types |
| ||||||||
| Parameters |
| ||||||||
| Maneuvers | |||||||||
| Orbital mechanics |
| ||||||||


 ,
,
 .
. ,
,



